Η παρακάτω είναι μια πραγματικά χρήσιμη άσκηση.
Ένα πολύγωνο του επιπέδου περιγράφεται μέσω της ακολουθίας των κορυφών του
,
όπου κάθε κορυφή συνδέεται με τις
.
Βρείτε ένα τύπο για το εμβαδό του μέσω των
,
.
Κατόπιν βρείτε κι ένα τύπο για το κέντρο βάρους του πολυγώνου (όχι των κορυφών του).
Για το εμβαδό:
Επιλέγουμε μία κορυφή, έστω τη (x_0, y_0) και φέρνουμε τις διαγωνίους από αυτήν. Υπολογίζουμε τις αποστάσεις d_i=[(x_0,y_0),(x_i,y_i)], i=1,2,…,N-1.
Θεωρούμε τα τρίγωνα με κορυφές τα σημεία (x_0,y_0), (x_i,y_i), (x_{i+1}, y_{i+1}), i=1,…,N-2.
Για καθένα από αυτά τα τρίγωνα μπορούμε να υπολογίσουμε το εμβαδόν του από τον τύπο του Ήρωνα, με την ημιπερίμετρο του. Δηλαδή, αν τ η ημιπερίμετρος ενός τριγώνου και α,β,γ τα μήκη των τριών πλευρών του, τότε το εμβαδόν του Ε είναι
Ε=[τ (τ-α) (τ-β) (τ-γ)]^{1/2}
Υπολογίζουμε οπότε το εμβαδόν για το καθένα από τα τρίγωνα και αθροίζουμε το συνολικό εμβαδό.
Σε περίπτωση που δεν είμαστε σίγουροι για το αν τα σημεία είναι ανά τρία μη συνευθειακά, μπορούμε να το ελέγξουμε αφού έχουμε υπολογίσει τα μήκη των τμημάτων που φέραμε, χρησιμοποιώντας την τριγωνική ανισότητα. Έστω ότι προκύπτουν τα (x_0,y_0),(x_i,y_i), (x_{i+1},y_{i+1}) συνευθειακά. Τότε θα θεωρήσουμε το τρίγωνο με κορυφές τα (x_0,y_0), (x_{i+1},y_{i+1}), (x_{i+2},y_{i+2}) και η διαδικασία συνεχίζεται ομοίως. Αν τελικά όλα είναι συνευθειακά, το εμβαδό θα είναι 0.
Μου αρέσει!Μου αρέσει!
Σχόλιο από vicky0 — 24 Μαρτίου, 2008 @ 10:28 μμ
vicky0:
Η διαδικασία που περιγράφεις θα δουλέψει αν το πολύγωνο είναι κυρτό και άρα τα τρίγωνά σου θα είναι ανά δύο ξένα και μπορείς συνεπώς να προσθέσεις τα εμβαδά τους. Δε δουλεύει στη γενική περίπτωση όπου τα τρίγωνα αυτά μπορούν να είναι αλληλοεπικαλυπτόμενα.
Στον τύπο που περιμένω να βρείτε μάλιστα δε χρειάζεται να χρησιμοποιήσει κανείς τετραγωνικές ρίζες ή άλλες πράξεις πέρα από τις συνήθεις αλγεβρικές πράξεις.
Think Green!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 24 Μαρτίου, 2008 @ 10:56 μμ
Χμμ.. Σωστά, είναι ειδική η περίπτωση.
Αν λοιπόν τελικά καταφύγουμε στον Green 🙂 , θα μας συμβουλεύσει να υπολογίσουμε το εμβαδό με τον εξής τύπο:
E = Σ (x_i * y_{i+1} – x_{i+1} * y_i)/2
Tο άθροισμα για i=0,1,…,N-1 θεωρώντας x_N=x_0, y_N=y_0.
Μάλιστα, ο τύπος αυτός θα μας δώσει το προσημασμένο εμβαδό. Δηλαδή, μπορεί να είναι αρνητικό, σε περίπτωση που οι κορυφές έχουν τοποθετηθεί δεξιόστροφα (στη φορά κίνησης των δεικτών του ρολογιού). Οπότε, μπορούμε εφόσον θέλουμε να θεωρήσουμε την απόλυτη τιμή αυτού.
Οι προηγούμενοι υπολογισμοί, θα μας δώσουν σχεδόν άμεσα και τις συντεταγμένες του κέντρου βάρους (x,y). Συγκεκριμένα,
x = Σ [(x_i + x_{i+1}) (x_i * y_{i+1} – x_{i+1} * y_i)]/ (6E)
και
y = Σ [(y_i + y_{i+1}) (x_i * y_{i+1} – x_{i+1} * y_i)]/ (6E)
με το i πάλι από 0 εώς N-1.
Μου αρέσει!Μου αρέσει!
Σχόλιο από vicky0 — 25 Μαρτίου, 2008 @ 12:48 πμ
vicky0:
Επειδή σε πολύ κόσμο μπορεί να φαίνεται μαγικό το πώς βρήκες αυτούς τους τύπους, ας θυμίσω τον τύπο του Green:
όπου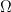 είναι ένα χωρίο στο επίπεδο και
είναι ένα χωρίο στο επίπεδο και  το σύνορό του προσανατολισμένο αριστερόστροφα και
το σύνορό του προσανατολισμένο αριστερόστροφα και  .
.
Για το εμβαδό του χωρίου έχουμε
με .
.
Για να καταλήξουμε στον τύπο που έδωσες αρκεί τώρα να σπάσουμε το επικαμπύλιο ολοκλήρωμα στα
στα  ευθύγραμμα τμήματα που το απαρτίζουν και έπειτα να παραμετρίσουμε με τον προφανή τρόπο το καθένα από αυτά και να υπολογίσουμε τη συμβολή του στο
ευθύγραμμα τμήματα που το απαρτίζουν και έπειτα να παραμετρίσουμε με τον προφανή τρόπο το καθένα από αυτά και να υπολογίσουμε τη συμβολή του στο  .
.
Για τον υπολογισμό του κέντρου βάρους η μέθοδος είναι η ίδια μόνο που αρχίζουμε τώρα όχι από το ολοκλήρωμα αλλά από τα
αλλά από τα  και
και  , και βρίσκουμε τα κατάλληλα ζεύγη
, και βρίσκουμε τα κατάλληλα ζεύγη  για να εφαρμόσουμε τον τύπο του Green.
για να εφαρμόσουμε τον τύπο του Green.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 25 Μαρτίου, 2008 @ 1:35 πμ
[…] πολυγώνου από τις συντεταγμένες των κορυφών (δείτε αυτό το post), και του έκανε πολύ μεγάλη εντύπωση ότι αυτή η μέθοδος […]
Μου αρέσει!Μου αρέσει!
Πίνγκμπακ από - Τα μαθηματικά είναι ο φίλος σας « Προβλήματα Μαθηματικών — 25 Μαΐου, 2008 @ 10:32 πμ