Πριν σας θέσω το νέο πρόβλημα θα σας πω μια ιστορία:
Πριν από καμιά 15αριά χρόνια ο αγαπημένος σας blogmaster ήταν μεταπτυχιακός φοιτητής και είχε ανάγκη από μερικά παραπάνω χρήματα απ’ αυτά που το Πανεπιστήμιο όπου σπούδαζε του έδινε, τα οποία ήταν μετρημένα ώστε να φτάνουν ακριβώς για να ζήσει κανείς με αξιοπρέπεια (κανονικοποιώντας πάντα το μέγεθος της αξιοπρέπειας λαμβάνοντας υπόψιν την ηλικία–οι ανάγκες μοιάζουν να είναι μονότονη συνάρτηση αυτής).
Καμιά δουλειά δεν είναι ντροπή, ειδικά αυτή που πληρώνει καλά, κι έτσι κατέληξε να δουλέψει με μια εταιρεία κι ένα εργαστήριο όπου δούλευαν κατά κανόνα μηχανικοί, και μάλιστα πολιτικοί μηχανικοί (με την ευρεία έννοια του όρου, μην πάει ο νους σας σε μπετά και σκαλωσιές κατ’ ανάγκη). Η δουλειά ήταν ενδιαφέρουσα και γιατί είχε να ασχοληθεί με κάποια προβλήματα αυτοματισμού (η πρόοδος προϋποθέτει τεμπέληδες, που βαριούνται να κάνουν με το χέρι πράγματα που θα έπρεπε να γίνονται από μηχανές) αλλά και γιατί ο φίλος σας ανάλωνε ένα σεβαστό κομμάτι του χρόνου του στο να κάνει κοινωνικής φύσης παρατηρήσεις. Αυτές αφορούσαν κυρίως τους διαφορετικούς τρόπους με τους οποίους οι μηχανικοί κι οι μαθηματικοί αντιμετώπιζαν τη δουλειά τους, σε τι έδιναν σημασία οι μεν κι οι δε και με τι προβλήματα ασχολούνταν.
Σε αυτή τη δουλειά ήταν που πρωτοχρειάστηκε να γράψει ένα πρόγραμμα που υπολόγιζε το εμβαδό πολυγώνου από τις συντεταγμένες των κορυφών (δείτε αυτό το post), και του έκανε πολύ μεγάλη εντύπωση ότι αυτή η μέθοδος φαινόταν να είναι άγνωστη στους συνεργάτες του μηχανικούς.
Εκεί όμως όπου έμεινε πραγματικά με το στόμα ανοιχτό ήταν όταν συνειδητοποίησε πώς διδάσκονταν οι φοιτητές μηχανικοί να υπολογίζουν ένα όγκο εκ περιστροφής, όπως αυτόν που φαίνεται παρακάτω.

(Αυτός ο όγκος αναπαριστούσε την τρύπα μιας εκσκαφής και σκοπός του μαθήματος ήταν να υπολογίσουν πόσο χώμα θα βγάλουν.) Λοιπόν ο καθηγητής δίδασκε τους φοιτητές του να σπάνε το στερεό αυτό σε κομμάτια με οριζόντιες τομές και κατόπιν να υπολογίζουν τον όγκο κάθε κομματιού γράφοντάς το σα προσημασμένο άθροισμα κώνων και κυλίνδρων. Π.χ. στο σχήμα επάνω η «μύτη» είναι κώνος και το από πάνω κομμάτι είναι διαφορά δύο κώνων κ.ο.κ. Έπειτα χρησιμοποιούσαν γνωστούς τύπους για όγκο αυτών το σχημάτων. Πράγμα φυσικά σωστό αλλά που είναι αρκετά δύσκολο να υπολογιστεί αυτόματα ή να καλύψει κάπως γενικότερες καταστάσεις.

Σας δίνεται ένα πολυγωνικό χωρίο 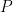 που περιέχεται στο δεξί ημιεπίπεδο
που περιέχεται στο δεξί ημιεπίπεδο  . Το πολύγωνο σας δίνεται με την ακολουθία
. Το πολύγωνο σας δίνεται με την ακολουθία  των κορυφών του. Βρείτε ένα τύπο για τον όγκο του στερεού που προκύπτει αν περιστρέψουμε το
των κορυφών του. Βρείτε ένα τύπο για τον όγκο του στερεού που προκύπτει αν περιστρέψουμε το 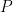 γύρω από τον άξονα
γύρω από τον άξονα 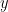 .
.







Πρέπει να έχετε συνδεθεί για να σχολιάσετε.