Ισόμορφα γραφήματα

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Πόσα μη-ισόμορφα γραφήματα μπορείτε να κατασκευάσετε για την ακολουθία βαθμών 4, 2, 2, 2, 1, 1;

Πόσα παιδιά είναι αγόρια;

Το πρώτο πρόβλημα είναι αρκετά γνωστό: συναντάμε στο δρόμο ένα φίλο μας από τα παλιά και μας λέει ότι έχει δύο παιδιά. Έχεις γιο; τον ρωτάμε. Έχω, μας απαντάει. Ποια η πιθανότητα να έχει δύο αγόρια;

Το δεύτερο είναι παρόμοιο: συναντάμε στο δρόμο ένα φίλο μας από τα παλιά και μας λέει ότι έχει δύο παιδιά. Έχεις γιο; τον ρωτάμε. Έχω, μας απαντάει, και έχει γεννηθεί Τρίτη. Ποια η πιθανότητα να έχει δύο αγόρια;

Συνάντησα το δεύτερο πρόβλημα για πρώτη φορά προχτές, και το εκπληκτικό είναι ότι η απάντηση δεν είναι η ίδια. (Υποθέτουμε ότι κάθε μια από τις δύο γέννες είναι εξίσου πιθανό να είναι αγόρι ή κορίτσι, ανεξάρτητα από την άλλη, και ότι όλες οι ημέρες της εβδομάδας είναι εξίσου πιθανές.)

Άθροισμα δυνάμεων

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Αν , και , βρείτε το .

O… τετραγωνισμός τού κύκλου (ή αντιστρόφως;)

Το πρόβλημα προτείνει ο Μάριος Γκρέτσα.

Δείξτε ότι το ανοιχτό μοναδιαίο τετράγωνο δε μπορεί να γραφτεί σαν ένωση κλειστών δίσκων οι οποίοι ανά δύο τέμνονται το πολύ σε ένα σημείο.

 

Άθροισμα περιοδικών συναρτήσεων

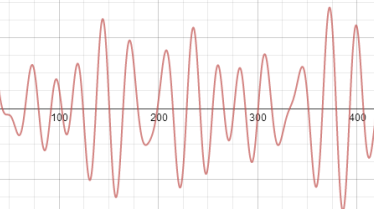
Ας είναι ένα πολυώνυμο με πραγματικούς συντελεστές. Δείξτε ότι μπορεί να γραφεί ως άθροισμα πεπερασμένου πλήθους περιοδικών συναρτήσεων του .

Πόσα μηδενικά;

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Ορίζουμε αναδρομικά μια ακολουθία ως εξής:

Θέτουμε , και για , αν υπάρχει τέτοιο ώστε , διαλέγουμε το μεγαλύτερο τέτοιο και θέτουμε , διαφορετικά . Είναι η ακολουθία φραγμένη;

Υπεργεωμετρική

Το πρόβλημα προτείνει ο Χρήστος Πελέκης.

Ένα δοχείο περιέχει κόκκινες και μπλε μπάλες. Επιλέγουμε ένα τυχαίο δείγμα μεγέθους , και έστω ο αριθμός των κόκκινων μπαλών. Τότε λέμε ότι η ακολουθεί την υπεργεωμετρική κατανομή με παραμέτρους και γράφουμε . Αν και , δείξτε ότι .

Δύο άγνωστοι αριθμοί

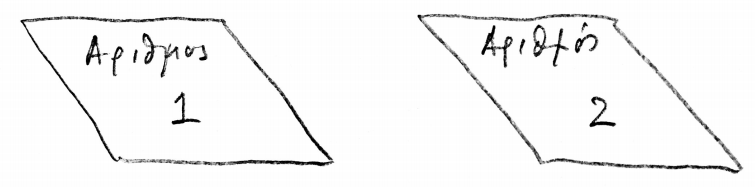
Κάτω από δύο χαρτάκια είναι γραμμένοι δύο διαφορετικοί πραγματικοί αριθμοί, άγνωστοι σε μας.

Διαλέγουμε στην τύχη ένα χαρτάκι, κοιτάμε τον αριθμό που λέει από κάτω, και κερδίζουμε μια καραμέλα αν δηλώσουμε σωστά ότι ο αριθμός που βλέπουμε είναι ο μεγαλύτερος ή ο μικρότερος από τους δύο.

Υπάρχει ένας εύκολος τρόπος να κερδίσουμε την καραμέλα με πιθανότητα 1/2. Ρίχνουμε ένα τίμιο νόμισμα και λέμε «μεγαλύτερος» ή «μικρότερος» ανάλογα με το τι έφερε το νόμισμα, κορώνα ή γράμματα. (Με αυτό τον τρόπο μάλιστα δε λαμβάνουμε καθόλου υπόψιν μας τον αριθμό που είδαμε γραμμένο κάτω από το χαρτάκι που διαλέξαμε.)

Υπάρχει τρόπος να παίξουμε αυτό το παιχνίδι έτσι η πιθανότητα να πάρουμε την καραμέλα να είναι μεγαλύτερη του 1/2;

Δίδυμοι πρώτοι

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης

 

Αποδείξτε πως όταν πολλαπλασιάσουμε οποιουσδήποτε δύο δίδυμους πρώτους (εκτός από μία περίπτωση), το αποτέλεσμα είναι πάντα αριθμός που δίνει υπόλοιπο 8 μετά από διαίρεση με το 9.

Αναδρομική ακολουθία

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Αν , , και ,  τότε μκδ και υπάρχει σταθερά ώστε για κάθε .

Διάσπαση ακολουθίας

To πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Λέμε ότι μια ακολουθία φυσικών χωρίς άσους επιδέχεται διχοτόμηση αν υπάρχει κάποια άλλη ακολουθία (φυσικών) τέτοια ώστε , όπου αναδιάταξη τής . Πότε μια ακολουθία τριών όρων επιδέχεται διχοτόμηση;

Breakeven

 

Το πρόβλημα προτείνει ο Χρήστος Πελέκης.

Η Alice και ο Bob παίζουν το ακόλουθο παιχνίδι. Πριν ξεκινήσουν, ο Bob καταβάλλει στην Alice το ποσό των USD. Στη συνέχεια, η Alice διαλέγει κρυφά ένα υποσύνολο με μέτρο , και ο Bob διαλέγει επίσης κρυφά σημεία . Μετά οι παίκτες αποκαλύπτουν τις επολογές τους, και η Alice καταβάλλει στον Bob το ποσό USD. Ποια τιμή τού κάνει το παιχνίδι δίκαιο;

Απλά γραφήματα

Την άσκηση (η οποία οφείλεται στον Adolph Winkler Goodman) προτείνει ο Κ. Κουρουζίδης.

Έστω ένα απλό γράφημα (χωρίς loops και περισσότερες από μια ακμές που να συνδέουν οποιεσδήποτε δύο κορυφές) με  κορυφές.

Έστω  ο συνολικός αριθμός τριγώνων στο και στο  (το γράφημα που είναι το συμπλήρωμα του ) μαζί.

Αποδείξτε ότι: ,

όπου:

 είναι το πλήθος των ακμών.

είναι το σύνολο των κορυφών του .

είναι η εκάστοτε κορυφή.

είναι ο βαθμός της εκάστοτε κορυφής.

 

Υπόδειξη: Αναλογιστείτε την συνεισφορά σε κάθε ακμή από κάθε τριάδα κορυφών.

 

Μια ταυτότητα

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Χρησιμοποιώντας πλήρη γραφήματα και βασικές αρχές απαρίθμησης αποδείξτε ότι

για .

 

Μήκος γραφήματος

Δείξτε ότι το μήκος τού γραφήματος μιας γνησίως αύξουσας συνάρτησης από το στο είναι το πολύ , και ότι το φράγμα αυτό «πιάνεται» από κάποια συνάρτηση. Ποιο είναι το καλύτερο άνω φράγμα για το μήκος τού γραφήματος μιας κυρτής συνάρτησης από το στο ;

Υπερκύβος

Tο πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Ο –διάστατος υπερκύβος είναι το γράφημα με σύνολο κομβών όλα τα δυαδικά διανύσματα μήκους . Δύο κόμβοι είναι συνδεδεμένοι με ακμή ακριβώς όταν διαφέρουν σε μία θέση οι συντεταγμένες τους. Ο γράφος ορίζεται αναδρομικά, αν πάρουμε δύο αντίτυπα μιας διάστασης μικρότερης (δηλαδή δύο ), θέσουμε την πρώτη συντεταγμένη του ενός αντιτύπου να είναι 0 και του δεύτερου 1, και ακολούθως ενώσουμε τις αντίστοιχες κορυφές. Θα μπορούσαμε όμως αυτό να το κάναμε με οποιαδήποτε άλλη από τη πρώτη συντεταγμένη, έτσι έχουμε συνολικά υποκύβους μιας διάστασης μικρότερης (Υποκύβος ονομάζεται οποιοσδήποτε υπερκύβος μικρότερης διάστασης που είναι υπογράφημα στο ).

Στο υπάρχουν υποκύβοι όλων των διαστάσεων, για . Πόσοι είναι αυτοί για κάθε ; Αν αθροίσουμε τις ακμές όλων των υποκύβων από έως , ποιό είναι το αποτέλεσμα;

Υποόδειξη: Υπολογίστε το ζητούμενο άθροισμα με τον προφανή τρόπο, αφού βρείτε πρώτα το πλήθος των υποκύβων διάστασης , και πόσες ακμές έχει οποιοδήποτε από τα . Ακολούθως εκφράστε ξανά το ζητούμενο άθροισμα, αναλογιζόμενοι το πόσες φορές προσμετράται μια οποιαδήποτε ακμή, χρησιμοποιώντας ένα συμμετρικό επιχείρημα. Απλοποιήστε. Τί παρατηρείτε;

 

Μπορείτε να σκοτώσετε τον ψύλλο;

Πάνω στο επίπεδο βρίσκεται ένας ψύλλος, ο οποίος είναι περιορισμένος να ζει και να κινείται πάνω στο σύνολο των ακεραίων σημείων του επιπέδου . Τη χρονική στιγμή 0 βρίσκεται στο σημείο και από κει και πέρα κινείται σε κάθε δευτερόλεπτο πηδώντας πάντα κατά το ίδιο διάνυσμα.

Με άλλα λόγια ο ψύλλος κινείται πάνω σε μια ευθεία και μάλιστα πάνω στα ακέραια σημεία της ευθείας αυτής, με σταθερή ταχύτητα. Για παράδειγμα θα μπορούσε σε κάθε ακέραια χρονική στιγμή να πηδάει κατά το διάνυσμα

.

Ο ψύλλος αυτός σας ενοχλεί και θέλετε να τον σκοτώσετε. Μπορείτε κάθε ακέραια χρονική στιγμή να χτυπάτε ένα από τα ακέραια σημεία του επιπέδου με την ελπίδα ότι ο ψύλλος βρίσκεται τότε εκεί και θα τον σκοτώσετε.

Δε βλέπετε όμως πού είναι ο ψύλλος (παρά μόνο αφού τον σκοτώσετε) ούτε ξέρετε ποιο είναι το διάνυσμα κίνησης του ψύλλου .

Μπορείτε να ακολουθήσετε μια μέθοδο χτυπημάτων που θα είναι σίγουρο ότι θα πετύχει τον ψύλλο αργά η γρήγορα; (Τη χρονική στιγμή 0 δε μπορείτε να χτυπήσετε. Αρχίζετε τη χρονική στιγμή 1.)

Έμαθα το πρόβλημα αυτό από τον Miklos Laczkovich.

Κοντά στη μετάθεση

Αν είναι μια συνάρτηση, για θέτουμε (η μετάθεση). Αν η είναι ολοκληρώσιμη και για κάποιο έχουμε για όλα τα , τότε σχεδόν παντού. Τι συμβαίνει αν ;

Γινόμενα Borel

Αν ο είναι ένας μετρικός χώρος με συμβολίζουμε τη σ-άλγεβρα των συνόλων Borel και με τη σ-άλγεβρα που παράγεται από όλα τα ορθογώνια όπου τα είναι Borel υποσύνολα τού . Δεν είναι δύσκολο να δει κανείς ότι

.

Ισχύει το ίδιο με ένα αυθαίρετο μετρικό χώρο στη θέση τού ;

Ορθοκανονικό σύνολο

Ας είναι ένα ορθοκανονικό υποσύνολο τού το οποίο αποτελείται από συνεχείς συναρτήσεις. Θέτουμε , όπου είναι η γραμμική θήκη. Δείξτε ότι αν υπάρχει σταθερά τέτοια ώστε

, τότε ο έχει πεπερασμένη διάσταση.