Κάτω από δύο χαρτάκια είναι γραμμένοι δύο διαφορετικοί πραγματικοί αριθμοί, άγνωστοι σε μας.
Διαλέγουμε στην τύχη ένα χαρτάκι, κοιτάμε τον αριθμό που λέει από κάτω, και κερδίζουμε μια καραμέλα αν δηλώσουμε σωστά ότι ο αριθμός που βλέπουμε είναι ο μεγαλύτερος ή ο μικρότερος από τους δύο.
Υπάρχει ένας εύκολος τρόπος να κερδίσουμε την καραμέλα με πιθανότητα 1/2. Ρίχνουμε ένα τίμιο νόμισμα και λέμε «μεγαλύτερος» ή «μικρότερος» ανάλογα με το τι έφερε το νόμισμα, κορώνα ή γράμματα. (Με αυτό τον τρόπο μάλιστα δε λαμβάνουμε καθόλου υπόψιν μας τον αριθμό που είδαμε γραμμένο κάτω από το χαρτάκι που διαλέξαμε.)
Υπάρχει τρόπος να παίξουμε αυτό το παιχνίδι έτσι η πιθανότητα να πάρουμε την καραμέλα να είναι μεγαλύτερη του 1/2;
Προβλήματα Μαθηματικών 
Έχουμε μαζί μας ένα φίλο μας, από τον οποίο ζητάμε να μας πει τυχαία ένα πραγματικό αριθμό. Συγκρίνουμε τον αριθμό που μας είπε, με τον αριθμό που
είναι γραμμένος κάτω από το χαρτάκι που διαλέξαμε (πάλι τυχαία) και πράτουμε ανάλογα.
Ενδεχομένως αυτή η στρατηγική να λειτουργήσει πιο ευεργετικά από το να πούμε τυχαία «μεγαλύτερος» ή «μικρότερος» (ακολουθώντας την ένδειξη του ζαριού).
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 4 Οκτωβρίου, 2019 @ 4:31 μμ
Θα ήθελα να «πάρω πίσω» το σχόλιο μου, μιας και δεν έχω πειστεί πως αυτό που προτείνω έχει ουσιαστική διαφορά από τη δουλειά που κάνει το τίμιο νόμισμα.
?
Το καίριο ερώτημα είναι άλλο όμως. Μπορεί κανείς να επιλέξει «στη τύχη» ένα οποιοδήποτε
Νομίζω πως μόνο σε φραγμένο διάστημα γίνεται.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 4 Οκτωβρίου, 2019 @ 7:53 μμ
Ναι, αν επιμένεις ο αριθμός που διαλέγεις να έχει ομοιόμορφη κατανομή («όλοι οι αριθμοί ισοπίθανοι», χονδρικά) τότε αυτό γίνεται μόνο σε φραγμένο διάστημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Οκτωβρίου, 2019 @ 8:35 πμ
Αυτό είναι πρόβλημα με θεωρία από πίσω;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 10:06 πμ
Μου φαίνεται αδύνατο και το σκέφτομαι ως εξής:
Η αντιστροφή προσήμου και στους δύο γραμμένους αριθμούς αντιστρέφει και τη σειρά ‘μικρότερος – μεγαλύτερος’. Αν όμως υπήρχε τρόπος να κερδίσουμε την καραμέλα με πιθανότητα πάνω από 1/2, αυτός θα έπρεπε να λειτουργεί ανεξάρτητα από το συνδυασμό προσήμων των δύο αριθμών, εφόσον κανένας τέτοιος συνδυασμός δεν είναι προτιμότερος από τον ‘αντίθετό του’. Αντίφαση, άρα το ζητούμενο δεν είναι εφικτό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 10:28 πμ
Θανάση, μπορούμε όμως να αγνοήσουμε εντελώς το παράγοντα «πρόσημο» νομίζω. Σκέψου πως υπάρχει ένα προς ένα αντιστοιχία μεταξύ του συνόλου
όλων των πραγματικών και του συνόλου όλων των μή αρνητικών. Άρα το πρόβλημα πάλι υφίσταται.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 10:42 πμ
Σύμφωνοι Κωνσταντίνε, υπάρχει τέτοια αντιστοιχία, π.χ. η αντιστοιχία των πραγματικών αριθμών με τις απόλυτες τιμές τους, αλλά δεν καταλαβαίνω πώς κάτι τέτοιο ακυρώνει το επιχείρημά μου. Αυτό που πρότεινα είναι η λήψη των αντιθέτων των δύο πραγματικών αριθμών, όχι των απόλυτων τιμών τους ή οτιδήποτε άλλο. Ξεκινώντας από ένα άγνωστο ζευγάρι πραγματικών, αντιστρέφοντας και τα δύο πρόσημα, πηγαίνω σε ένα απολύτως ισοπίθανο με το αρχικό νέο ζευγάρι πραγματικών (όχι απαραιτήτως μη αρνητικών), με αντεστραμμένη όμως τη σχέση μικρότερου – μεγαλύτερου..
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 12:41 μμ
5,7: Δε βλέπω που είναι η αντίφαση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 8 Οκτωβρίου, 2019 @ 12:45 μμ
Τότε δεν θα υπάρχει😊.
Θεώρησα ότι πάλι μαντεύουμε χωρίς να δούμε τον ένα αριθμό, αλλά αυτό είναι ήδη παρατημένο..
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 1:45 μμ
Απαντημένο, όχι παρατημένο, ανορθόγραφε!
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 2:22 μμ
Αν ξέραμε ότι οι αριθμοί ανήκουν σε κάποιο πεπερασμένο διάστημα (α,β), κατανέμονται ομοιόμορφα σε αυτό και στο χαρτί που κοιτάζουμε είναι γραμμένος ο αριθμός χ, τότε η πιθανότητα ο άλλος αριθμός να είναι μικρότερος του χ θα ήταν (χ-α)/(β-α) και η πιθανότητα να είναι μεγαλύτερος του χ θα ήταν (β-χ)/(β-α). Σε τέτοια περίπτωση θα μπορούσαμε να διαλέξουμε το ενδεχόμενο που μας δίνει τη μεγαλύτερη από τις δύο πιθανότητες.
Δεν το ξέρουμε όμως..
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 2:58 μμ
Γιατί όμως Κωνσταντίνε πήρες πίσω το πρώτο σου σχόλιο; Μου φαίνεται ότι δίνει πιθανότητα 1 αν συμβεί ο αριθμός του φίλου να είναι ανάμεσα στους δύο γραμμένους και 1/2 σε διαφορετική περίπτωση. Αυτό δεν είναι κάτι παραπάνω από 1/2 μεσοσταθμικά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 3:58 μμ
Θα ξανασκεφτώ το πρόβλημα, μαζί με τα δικά σου σχόλια. Δεν έχω απάντηση τώρα. Δε ξέρω επίσης αν υπάρχει deep theory που κρύβει το πρόβλημα, αλλά αυτό
θα το ξέρει ο καθηγητής.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 4:19 μμ
12: «Μου φαίνεται ότι δίνει πιθανότητα 1 αν συμβεί ο αριθμός του φίλου να είναι ανάμεσα στους δύο γραμμένους και 1/2 σε διαφορετική περίπτωση.» Είσαι σίγουρος
γι’αυτό; Δε νομίζω.
Επίσης, αν νομίζεις πως δε γίνεται να υπάρχει στρατηγική, θα πρέπει να δείξεις με μαθηματικά πως όντως δεν υπάρχει. Και να είσαι σίγουρος για την απόδειξη σου.
Εγώ δε βλέπω πως να αντιμετωπίσω το πρόβλημα. Να πώ όμως πως διαισθητικά συμφωνώ μαζί σου πως η απάντηση στο πρόβλημα μάλλον είναι: Όχι.
Επίσης, όσων αφορά τα σχόλιά μας, καλύτερα να περιμένουμε απάντηση από τους μπλόκ-μάστερς.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 7:36 μμ
Το ‘μου φαίνεται’ ήταν σχήμα λόγου, αφού η ιδέα ήταν δική σου και φαντάστηκα ότι θα την απέρριπτες ή θα την ολοκλήρωνες ο ίδιος μαθηματικά.
Αν ο αριθμός του φίλου είναι μεταξύ των δύο γραμμένων, τότε αν ο αριθμός που κοίταξα είναι μικρότερος του αριθμού του φίλου, κοίταξα τον μικρότερο, αλλιώς κοίταξα τον μεγαλύτερο από τους δύο γραμμένους. Σε κάθε περίπτωση απαντώ σωστά με πιθανότητα 1.
Αν ο αριθμός του φίλου είναι μεγαλύτερος ή μικρότερος και από τους δύο γραμμένους, απαντώ σωστά με πιθανότητα 1/2, αφού τότε κοίταξα ισοπίθανα τον μεγαλύτερο ή το μικρότερο από τους δύο γραμμένους.
Εξακολουθώ πάντως, αν επιτρέπεις, να έχω επιφύλαξη για τη σύνθεση των δύο περιπτώσεων σε πιθανότητα μεγαλύτερη του 1/2.
Αν καταλαβαίνω σωστά πάντως το τι συνιστούν να γράφουμε στα σχόλια οι blog masters, οι κανόνες δεν είναι τόσο σκληροί όσο τους περιγράφεις😊.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Οκτωβρίου, 2019 @ 9:13 μμ
Να μου επιτρέψεις αγαπητέ κ. Παπαδημητρίου να γίνω «μαθηματικά αυστηρός» τώρα. Το εύρος των πραγματικών αριθμών είναι προκαθορισμένο;
Για να είμαι ειλικρινής το πρώτο μου σχόλιο είχε χιούμορ, to get the ball rolling, regarding the problem. Στο δεύτερο ρώτησα, γιατί μια φορά,
μου έκανε μαθηματική παρατήρηση ο Δρ Πελέκης, πως πάντα στο μυαλό μας όταν διαλέγουμε ένα αριθμό «τυχαία» πρέπει να έχουμε υπόψιν
σε ποιό χώρο δουλεύουμε και να γνωρίζουμε ως προς ποιό «μέτρο». (measure) Από τότε έγινα ιδιαίτερα επιφυλακτικός. Τώρα αν κάποτε κάποιο σχόλιο μου
μεταξύ σοβαρού και αστείου έχει δόση αλήθειας, αυτό ελπίζω (τουλάχιστον), να μην είναι τυχαία(!)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 9:33 μμ
«Αν ο αριθμός του φίλου είναι μεταξύ των δύο γραμμένων, τότε αν ο αριθμός που κοίταξα…»
«Αν ο αριθμός του φίλου είναι μεγαλύτερος ή μικρότερος και από τους δύο γραμμένους…»
Έχεις υπόψιν πως το δεύτερο χαρτάκι ΔΕ το γυρνάς;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 10:17 μμ
Το ‘μου φαίνεται’ που έγραψες πιο πάνω δε το έκρινα καθόλου, ούτε όταν το έβαλα σε εισαγωγικά εγώ. Απλά δε κατάλαβα το επιχείρημα γι’αυτό σε ρώτησα αν είσαι
σίγουρος..
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 10:19 μμ
Δε μπορούμε να ξέρουμε apriori καθόλου πού κοντά είναι το δεύτερο χαρτάκι σε σχέση με το πρώτο, οπότε έχει νόημα να πάρουμε περιπτώσεις;;
Professor ;;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Οκτωβρίου, 2019 @ 10:21 μμ
15: Σκέψου το ως εξής. Άλλαξε το ρόλο του δεύτερου χαρτιού με το πρόσωπο που σου λέει ένα αριθμό τυχαία; Λογικά δεν έπρεπε να υπάρχει διαφορά..
. Συμπληρωματικά ξένα ενδεχόμενα που καλύπτουν όλο το χώρο έχουν άθροισμα ένα.
Έπειτα
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 12:45 πμ
Υπόδειξη: Είναι δυνατόν να απαντήσουμε σωστά με πιθανότητα μεγαλύτερη του 1/2. Το πόσο μεγαλύτερη δε μπορούμε να το ξέρουμε εκ των προτέρων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Οκτωβρίου, 2019 @ 6:40 πμ
Αρκεί να σκεφτούμε / υποθέσουμε ότι ο αριθμός του φίλου, ανεξαρτήτως τύπου και παραμέτρων κατανομής, έχει πιθανότητα p>0 να βρεθεί ανάμεσα στους δύο γραμμένους.
Η πιθανότητα επιτυχίας της στρατηγικής είναι:
p*1+(1-p)*1/2 = (1+p)/2 > 1/2
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 9 Οκτωβρίου, 2019 @ 9:20 πμ
22: Θα μπορούσατε να ξαναγράψετε συνολικά τη μέθοδο γιατί έχω χαθεί λίγο με όσα έχουν γραφτεί παραπάνω;
Μου αρέσει!Αρέσει σε 1 άτομο
Σχόλιο από Mihalis Kolountzakis — 9 Οκτωβρίου, 2019 @ 9:23 πμ
22: Θανάση γράψτην εσύ σε παρακαλώ. Είσαι πολύ καλύτερος λύτης από μένα 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 9:38 πμ
Τώρα κάνω το γραφιά του Κωνσταντίνου, αλλά χαλάλι του😊:
Ζητάμε από ένα φίλο να μας πει έναν τυχαίο πραγματικό αριθμό.
Αφού μας τον πει, ανοίγουμε το ένα χαρτί στην τύχη και κοιτάμε τον αριθμό που είναι γραμμένος.
Αν ο αριθμός που βλέπουμε είναι μικρότερος του αριθμού που μας είπε ο φίλος, μαντεύουμε ότι ο αριθμός που είδαμε είναι ο μικρότερος, αλλιώς μαντεύουμε ότι είναι ο μεγαλύτερος από τους δύο γραμμένους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 9 Οκτωβρίου, 2019 @ 10:19 πμ
25: Και τυχαίος πραγματικός αριθμός σημαίνει τι στη μέθοδο αυτή;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Οκτωβρίου, 2019 @ 11:11 πμ
Μάλλον ανήκει σε διάστημα της μορφής [ ) , ( ] , ( ) , ή [ ] όπου στο ένα άκρο ένας πραγματικός α , στο άλλο ένας β, όπου φυσικά
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 1:22 μμ
Και πού ξέρετε ποια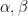
να πάρετε;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Οκτωβρίου, 2019 @ 1:25 μμ
Η άσκηση δε δίνει αρκετές πληροφορίες έχω την εντύπωση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 1:47 μμ
Τώρα έχω μια ιδέα. Να το σκεφθώ..
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 1:49 μμ
Αν καταλαβαίνω σωστά το ερώτημα, θα έλεγα ότι ζητάμε από το φίλο να μας πει (ή σκεφτόμαστε οι ίδιοι) έναν πραγματικό αριθμό / τιμή τυχαίας μεταβλητής που ακολουθεί οποιαδήποτε συνεχή κατανομή πιθανότητας, αρκεί αυτή να αποδίδει μη μηδενική πιθανότητα σε κάθε πραγματικό αριθμό ή διάστημα (π.χ. μια κανονική κατανομή).
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 9 Οκτωβρίου, 2019 @ 2:29 μμ
Εμένα μου πέρασε απ’το μυαλό ότι το πρόβλημα Breakeven ίσως να έχει σχέση. Μήπως οι αριθμοί (και οι δύο !) που είναι γραμμένοι
είναι υπό κάλυψη «παίκτης» , και εμείς πρέπει να τυχαιοποιήσουμε το τρόπο που παίζουμε ώστε να έχουμε παραπάνω από 1/2 chance
να νικήσουμε;; Εννοείται εξακολουθούμε να έχουμε το παρέα μας.. Τί λέτε παιδιά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 2:43 μμ
31: Σωστά. Για να μη μείνει καμιά αμφιβολία για τη μέθοδο την ξαναγράφω εδώ.
Ας είναι
οι άγνωστοι σε μας κρυμμένοι αριθμοί. Παίρνουμε μια συνεχή πυκνότητα πιθανότητας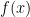 
που δε μηδενίζεται πουθενά (π.χ. η κανονική κατανομή αλλά υπάρχουν φυσικά και πολλές άλλες) και εκτελούμε ένα πείραμα που μας δίνει ένα αποτέλεσμα 
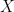που ακολουθεί την κατανομή της 
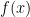. Έπειτα (ή και πριν, δεν έχει σημασία) αποκαλύπτουμε τυχαία έναν από τους δύο αριθμούς και ας πούμε 
αυτό που είδαμε (το 
λοιπόν είναι μια τυχαία μεταβλητή που παίρνει δύο τιμές, τις 
με ίση πιθανότητα.
Αν
απαντάμε ότι ο αριθμός που είδαμε είναι ο μεγαλύτερος, αλλιώς απαντάμε ότι είναι ο μικρότερος.
Απαντάμε έτσι σωστά με πιθανότητα
. Αυτό οφείλεται στο ότι το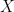 
πέφτει ανάμεσα στα 
με θετική πιθανότητα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Οκτωβρίου, 2019 @ 3:08 μμ
Μπορείτε να μας εξηγήσετε λίγο περισσότερο το τί θα πει: To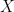
«πέφτει» ανάμεσα στα 
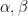με θετική πιθανότητα ;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 3:48 μμ
Επίσης πού κυμαίνονται οι τιμές της
;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 4:06 μμ
Ο.Κ. Το 31, απαντάει στο ερώτημά μου. Cheers.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 9 Οκτωβρίου, 2019 @ 5:00 μμ
Διαπίστωσα πως μια τουλάχιστον εξίσου εποικοδομητική συζήτηση μπορεί να βρει ο αναγνώστης στο facebook του καθηγητή μας.
Υπάρχουν περαιτέρω διευκρινίσεις, και κάποιος έκανε μέχρι και αριθμητική προσομοίωση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Οκτωβρίου, 2019 @ 9:31 μμ
Αναρωτιέμαι τι θα ήταν λάθος στην παρακάτω προσέγγιση ας πούμε:
( διαισθάνομαι ότι κάτι είναι μάλλον λάθος …)
Επιλέγουμε το 0 λόγω συμμετρίας . Αν ο αριθμός που σηκώνουμε είναι μεγαλύτερος (ή ίσος με) από το 0 ,λέμε ότι είναι ο μεγαλύτερος. Αν είναι αρνητικός λέμε ότι είναι ο μικρότερος.
Η πιθανότητα και οι δυο αριθμοί να είναι μικρότεροι από 0 είναι 1/4, οπότε η πιθανότητα να πούμε σωστά ότι ο ένας εκ των δυο είναι ο μικρότερος είναι 1/2 , άρα 1/8 ολική πιθανότητα . Στην περίπτωση 2 θετικών ομοίως συνολική πιθανότητα σωστής μαντεψιάς 1/8.
Η πιθανότητα οι δυο αριθμοί να είναι ετεροπρόσημοι είναι 1/2., και σ αυτήν την περίπτωση η πιθανότητα η δηλωσή μας να είναι σωστή είναι 1.
Οπότε η ολική πιθανοτητα είναι: 1/2+1/8+1/8=3/4
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 1:22 μμ
38: Το μόνο τυχαίο σε αυτό το πρόβλημα είναι το ποιο χαρτάκι επιλέγουμε. Οι αριθμοί
μας είναι άγνωστοι αλλά δεν είναι τυχαίοι. Δεν έχει λοιπόν νόημα να μιλήσουμε όπως στο: «Η πιθανότητα και οι δυο αριθμοί να είναι μικρότεροι από 0 είναι 1/4».
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Νοεμβρίου, 2021 @ 3:20 μμ
39. Ευχαριστώ Μιχάλη για την απάντηση! Πώς «παράγονται» οι αριθμοί a και b ? Κάπου μπερδεύομαι (έχω ψιλλοπαρατήσει και το «σπορ»…) αν δεν είναι τυχαίοι;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 3:34 μμ
40: Οι αριθμοί
δεν παράγονται από κάπου. Είναι δύο σταθεροί αριθμοί. Όποιοι και να είναι αυτή η πιθανότητα να δουλέψει η μέθοδος που δώσαμε επιτυγχάνει με πιθανότητα > 1/2. Το πόσο μεγαλύτερη είναι του 1/2 εξαρτάται και από τα 
αλλά και από την κατανομή που επιλέξαμε στη μέθοδό μας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Νοεμβρίου, 2021 @ 4:09 μμ
Διαβάζοντας ξανά προσεκτικά τα σχόλια παραπάνω , κατάλαβα το λαθος μου. Έχει να κάνει με το ότι δεν μπορούμε στην πραγματικότητα να έχουμε random αριθμούς, αλλά μόνο pseudo random. Σωστά;
Οπότε η μόνη πιθανότητα για την οποία έχει νόημα να μιλάμε είναι η πιθανότητα κάποιο σημείο /αριθμός να κειται μεταξύ δυο άλλων . Σ ένα διάστημα. Κι αυτή δίνεται απ το ολοκληρώμα της πυκνότητας πιθανότητας (probability density) που ειναι σ αυτήν την περίπτωση μια ομοιόμορφη κατανομή μεταξύ αυτών των δυο ορίων.
Μ αλλά λόγια , η πιθανότητα 0,75 θα ίσχυε μόνο σε κάποιο countable σύνολο. Αν οι αριθμοί ήταν ας πούμε ακέραιοι. Σωστά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 4:14 μμ
42: Όχι. Οι αριθμοί που χρησιμοποιούμε (που αντλούμε από την κατανομή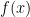
) είναι τυχαίοι αριθμοί, όχι ψευδο-τυχαίοι. Το αν γενικά υπάρχει κάτι τυχαίο σε αυτό το σύμπαν ή όχι είναι άλλο ερώτημα και δεν έχει νόημα να μπούμε εδώ σε αυτό. Αλλά ναι, υποθέτουμε άπειρη ακρίβεια στην αναπαράσταση του αριθμού που αντλούμε.
Δε βλέπω να αλλάζει κάτι στο πρόβλημα αν υποθέσουμε εξαρχής ότι
οπότε σε αυτή την περίπτωση θα μας αρκούσε μια πυκνότητα πιθανότητας πάνω σε όλους τους ακεραίους (με θετική πυκνότητα σε κάθε ακέραιο). Σε αυτή την περίπτωση οι τυχαίοι αριθμοί που χρησιμοποιεί η μέθοδός μας είναι ακέραιοι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Νοεμβρίου, 2021 @ 4:20 μμ
Τώρα ξαναμπερδεύτηκα…
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 4:29 μμ
Άκυρο το 44. Όλα οκ. Ευχαριστίες στο Μιχάλη (και στο Θανάση , το σκιώδη μου σύμβουλο! 😊 )
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 5:54 μμ
45: Πονηρό πράγμα οι πιθανότητες. Αλλά και από τα ωραιότερα μαθηματικά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Νοεμβρίου, 2021 @ 6:00 μμ
Μια και το ξαναθυμηθήκαμε, ας το τραβήξω λίγο ακόμα..
Ο φίλος Γιώργος μάς λέει ότι αν οποιοσδήποτε από τους αριθμούς α,β είναι μεγαλύτερος του 0, τότε ο άλλος έχει διπλάσια πιθανότητα να είναι μικρότερος (ή ίσος) του 0 παρά να είναι κι αυτός μεγαλύτερος του 0.
Ο αριθμός 0 όμως δεν μας λέει κανείς πως έχει αυτή την προνομιούχα θέση στο σύνολο των πραγματικών αριθμών, ακέραιων ή ό,τι άλλο, σε σχέση τουλάχιστον με την πιθανή θέση των α,β ως προς αυτόν. Θα μπορούσε δηλαδή κάποιος, ας πούμε ο Θανάσης, να βάλει στη θέση τού 0 οποιονδήποτε πραγματικό (π.χ. τον 10^1000) και να σκεφτεί ότι αν οποιοσδήποτε από τους αριθμούς α,β είναι μεγαλύτερος του 10^1000, τότε ο άλλος έχει διπλάσια πιθανότητα να είναι μικρότερος (ή ίσος) του 10^1000 παρά να είναι κι αυτός μεγαλύτερος του 10^1000. Έτσι αν εμφανιστεί στο χαρτάκι που ανοίγεται οποιοσδήποτε αριθμός στο διάστημα (0,10^1000), ο μεν Γιώργος θα πει ότι είναι ο μεγαλύτερος, ο δε Θανάσης θα πει ο μικρότερος, θεωρώντας και οι δύο πώς λένε το σωστό με πιθανότητα 3/4.
Δύσκολο..😊
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 28 Νοεμβρίου, 2021 @ 8:13 μμ
Θανάση, καταρχάς σ ευχαριστώ για την επικοινωνία που είχαμε μετά από καιρό, χάρηκα πραγματικά, και για την πρόταση-βοήθειά σου. Απλώς ,επειδή με έβαλες συν-πρωταγωνιστή στο σενάριο του dumb & dumber από πάνω ,με εμένα σκηνοθέτη και στο ρόλο του dumber ομού 🥴 να πούμε προς ελάφρυνση της οπωσδήποτε βεβαρημένης θέσης μου ότι δεν πρόκειται για κάποιου είδους fallacy η συλλογιστική μου , και θα ήταν έγκυρη αν οι αριθμοί A και Β ήταν random. Αν ήταν uniformly ,independently randomized from R. Συμφωνείς νομίζω.
Η διευκρίνιση βέβαια του Μιχάλη ότι δεν είναι random , αλλάζει βεβαίως το πρόβλημα και με αφήνει έωλο και καταγέλαστο, τι να πω! 😊
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 28 Νοεμβρίου, 2021 @ 11:41 μμ
Γιώργο, ανακαλώ το αχρείαστο σχόλιό μου και σού ζητώ συγγνώμη, αν και δεν είχα πρόθεση να προκαλέσω αρνητικούς συνειρμούς ή απαξία (θα έπρεπε όμως να μου έχει περάσει από το μυαλό..)
Στην ουσία: Δεν μπορώ παρά να συμφωνήσω ότι οι α,β δεν είναι random, αφού δεν θα μπορούσαν (νομίζω) να προκύψουν από μια τέτοια διαδικασία, χωρίς να έχει οριστεί κάποιο πεπερασμένο διάστημα που να τους περιέχει. Πώς θα μπορούσε λοιπόν η συλλογιστική σου να είναι έγκυρη..
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 29 Νοεμβρίου, 2021 @ 2:06 πμ
Όχι βρε Θανάση, με παρεξήγησες. Ούτε κατά διάνοια δεν εισέπραξα απαξία απ το σχόλιό σου ξέρω τι άνθρωπος είσαι ! Απλώς είναι αυτή η παλιά μου «αδυναμία» να μην μπορώ εύκολα να αντιμετωπίσω το «εν δυνάμει» και το «εν ενεργεία» άπειρο , και έτσι -παρα την ακλόνητη κατάρριψη που μου έστειλες στο μέηλ , κάτι ακόμα με «έτρωγε» ψες βράδυ… Εγώ θα έπρεπε λοιπόν να ανακαλέσω το σχόλιο 11.41. Το ξανασκέφτηκα σαν ένα πιο εποπτικό γεωμετρικό ανάλογο , έναν «τροχό της τύχης» που γυρνάει και που όπως όλοι ξέρουμε η γεωμετρική πιθανότητα να σταματήσει κάπου έχει νόημα μόνο σαν ratio εμβαδών και ποτέ δεν μπορούμε να ορίσουμε “κατώφλια» thresholds μεμονωμένων σημείων. Είναι το ίδιο (νομίζω) . Αν μας πούνε ότι κάτω απ τα χαρτάκια είναι 2 σημεία του κύκλου , τι λες;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 29 Νοεμβρίου, 2021 @ 9:17 πμ
Δεν καταλαβαίνω ομολογώ, αν υποθέταμε ότι οι α,β μπορούσαν να είναι αριθμοί uniformly independently randomised from R (!), πώς θα μπορούσαν να παραχθούν από τον ‘τροχό της τύχης’, αν κάθε αριθμός όπου θα μπορούσε να ‘κάτσει’ ο τροχός έπρεπε να έχει ίση θετική πιθανότητα με κάθε άλλον.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 29 Νοεμβρίου, 2021 @ 11:52 πμ
51: Δεν είναι δυνατό να έχει κανείς τυχαίους αριθμούς σε όλο το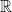
και να έχουν όλα τα διαστήματα μήκους 1, π.χ., την ίδια πιθανότητα. Επίσης δεν είναι δυνατό να έχει κάθε πραγματικός αριθμός θετική πιθανότητα να εμφανιστεί.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Νοεμβρίου, 2021 @ 7:26 μμ
Σημαντικό το point.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 7 Δεκεμβρίου, 2021 @ 1:52 μμ
Μια πρόχειρη απόδειξη γι’ αυτό, που θα ικανοποιούσε ίσως και το φίλο Γιώργο:
Αν υπήρχε τέτοια δυνατότητα, θα έπρεπε, να υπάρχει συνάρτηση πυκνότητας πιθανότητας f(x) ώστε:
το ολοκλήρωμα f(x)dx από -∞ έως +∞ = 1
Για να έχει κάθε πραγματικός την ίδια πιθανότητα εμφάνισης, θα έπρεπε f(x)=σ (σ: μη αρνητική σταθερά).
Το πιο πάνω ολοκλήρωμα, αν σ>0, απειρίζεται, ενώ αν σ=0 μηδενίζεται, δηλαδή δεν μπορεί να είναι ίσο με 1.
Επομένως δεν υπάρχει έγκυρη ομοιόμορφη κατανομή πιθανότητας στο σύνολο του R.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 7 Δεκεμβρίου, 2021 @ 4:44 μμ
Θανάση, είμαι χαρούμενος που η αρχική μου εισήγηση στο πρώτο σχόλιο ήτανε σωστή. Η δύναμη της διαίσθησης στα μαθηματικά είναι μεγάλη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 7 Δεκεμβρίου, 2021 @ 10:17 μμ
Πράγματι Κωνσταντίνε, τα δύο πρώτα σχόλιά σου ήταν ο οδηγός για τη λύση, ήταν η μισή λύση νομίζω!
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 7 Δεκεμβρίου, 2021 @ 10:46 μμ
Αλλά ήταν vague. Μετά το συνειδητοποίησα πως είχε βάση η ιδέα αφού έγραψε τη λύση ο καθηγητής! Μάλλον ήταν απλή τύχη στη περίπτωσή μου 🙂 Δεν πειράζει. Η καλή τυχη παντού χρειάζεται…
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 7 Δεκεμβρίου, 2021 @ 11:16 μμ
40: Ελπίζω να επανέλθει σύντομα στο «άθλημα» ο κ. Ριζόπουλος. Είναι από τα δυσκολότερα… Μην εγκαταλείπουμε τα μαθηματικά!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 7 Δεκεμβρίου, 2021 @ 11:20 μμ
Test
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 15 Δεκεμβρίου, 2021 @ 1:06 μμ