Προβλήματα Μαθηματικών

10 Μαΐου, 2019

Αναδρομική ακολουθία

Filed under: Άλυτα Προβλήματα — Themis Mitsis @ 4:34 μμ

Το πρόβλημα προτείνει ο Κωνσταντίνος Κουρουζίδης.

Αν s_0=4, s_1=6, και s_{i+1}=is_i+s_{i-1},  τότε μκδ(s_{i+1},s_{i})=2 και υπάρχει σταθερά C>0 ώστε s_i<Ci! για κάθε i.

4 Σχόλια »

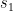  1. Αν κάποιο p διαιρεί τα s_i και s_{i+1} , τότε διαιρεί και το s_{i+1} - is_i = s_{i-1} . Άρα επαναλαμβάνοντας το επιχείρημα διαιρεί και τα s_0 και s_1 . Άρα p=1 ή p=2. Οι όροι της ακολουθίας είναι όλοι ζυγοί άρα μκδ=2.

    Για το δεύτερο ερώτημα πάμε επαγωγικά. Καταρχάς η ακολουθία είναι αύξουσα. Έστω για κάποιο c ισχύει

    s_i < Ci! . Είναι s_{i+1} = is_i + s_{i-1} < iCi! + s_i < iCi! + Ci! = C(i+1)!

    Η ύπαρξη σταθεράς για i = 0 και 1 είναι προφανής (π.χ. C=7)

    Μου αρέσει!

    Σχόλιο από shortmanikos — 18 Οκτωβρίου, 2019 @ 3:58 μμ

  2. Τί εννοείς για το δεύτερο μέρος «πάμε επαγωγικά». Πρέπει να δείξεις την ύπαρξη της σταθεράς, όχι να υποθέσεις ότι υπάρχει…

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 18 Οκτωβρίου, 2019 @ 10:44 μμ

  3. Συγγνώμη, είναι τελείως άκυρο αυτό που έγραψα παραπάνω. Σωστή η λύση.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Οκτωβρίου, 2019 @ 12:53 μμ

  4. I_n(z)=\frac{1}{2\pi i} \oint e^{(z/2)(t+\frac{1}{t})}t^{-n-1} \,dt where the contour encloses the origin and is traversed in a counterclockwise direction.
    K_n(x)=\frac{\pi}{2} \frac{I_{-n}(x)-I_{n}(x)}{sin(n\pi)}. Οι όροι της αναδρομικής μας ακολουθίας, χρησιμοποιώντας τις πιο πάνω φόρμουλες
    δίνεται από τον ακόλουθο τύπο: S_n=\left(8K_1(2)-12K_0(2)\right)I_n(-2)+4\left(3I_0(2)+2I_1(2)\right)K_n(2).

    Αφού δείξετε αναλυτικά το πώς θα υπολογίζατε το I_6(-2), ακολούθως υπολογίστε χρησιμοποιώντας τους πιο πάνω τύπους
    το S_6.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 20 Οκτωβρίου, 2019 @ 7:54 μμ


RSS feed for comments on this post. TrackBack URI

Σχολιάστε

Blog στο WordPress.com.