Σας δίνεται ένα άπειρο πλήθος από ίδια ορθογώνια τούβλα, διαστάσεων cm.
Δείξτε ότι μπορείτε να φτιάξετε μία στήλη από αυτά η οποία
- να ισορροπεί,
- να έχει ένα τούβλο σε κάθε οριζόντιο επίπεδο και
- προβαλλόμενη κατακόρυφα κάτω να φτάνει 100 m μακριά.
Προσπαθείστε να δώσετε μια λύση χωρίς πράξεις, στηριζόμενοι σε «φυσικά» επιχειρήματα.
Υπόδειξη
Υποθέστε ότι κάποιος σας δίνει μια στήλη από τούβλα η οποία ισορροπεί και όταν προβληθεί κάτω φτάνει σε απόσταση .
.
Δείξτε ότι μπορείτε, χρησιμοποιώντας αυτή τη στήλη, να φτιάξετε μια άλλη στήλη που ισορροπεί και η οποία όταν προβληθεί κάτω να φτάνει σε απόσταση .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 24 Μαρτίου, 2008 @ 12:01 μμ
Συνέχεια προηγούμενης υπόδειξης:
1. Χρησιμοποιείστε την υπάρχουσα στήλη ως το πάνω κομμάτι της νέας σας κατασκευής.
2. Είναι πολύ δύσκολο να επηρεάσετε την ισορροπία ενός ελέφαντα αν τον φορτώσετε επιπλέον με ένα φτερό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Απριλίου, 2008 @ 9:05 μμ
Συνέχεια προηγούμενης υπόδειξης:
3. Στη νέα σας κατασκευή θα έχετε δύο κομμάτια, το κάτω και το πάνω. Το πάνω κομμάτι θα είναι η προηγούμενή σας κατασκευή (που η προβολή της φτάνει σε απόσταση ). Το κάτω θα είναι μια κατακόρυφη στήλη από πάρα πολλά τούβλα.
). Το κάτω θα είναι μια κατακόρυφη στήλη από πάρα πολλά τούβλα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Ιουνίου, 2008 @ 8:37 μμ
Αν μαντεύω σωστά τη λύση που προτείνει ο κύριος
Κολουντζάκης, τότε η υπόδειξη για τον ελέφαντα και το x+1 είναι περισσότερο παραπλανητικές, ενώ
η κατακόρυφη στήλη από τούβλα δίνει την
εντύπωση ότι είναι εντελώς κατακόρυφη, πράγμα
που δεν ισχύει θεωρητικά.
Η υπόδειξη για τη χρήση της υπάρχουσας στήλης
σαν το πάνω κομμάτι της νέας κατασκευής
είναι πιστεύω υπέρ-αρκετή. Ωστόσο χρειάζονται
κάποιες απλές πράξεις για να δικαιολογήσουμε
τα «φυσικά» επιχειρήματα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 12 Αυγούστου, 2008 @ 10:58 μμ
Δηλαδή;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 12 Αυγούστου, 2008 @ 11:00 μμ
Δηλαδή για πιο απ’ όλα?
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 12 Αυγούστου, 2008 @ 11:23 μμ
Ποια είναι τα φυσικά επιχειρήματα και ποια είναι η λύση;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 12 Αυγούστου, 2008 @ 11:25 μμ
Καταρχήν πρέπει να ερμηνεύσουμε κατάλληλα
την υπόδειξη για τη νέα κατασκευή. Προφανώς
εννοείτε ότι πρέπει να σηκώσουμε τη στήλη
που ισορροπεί και να τοποθετήσουμε από
κάτω το επόμενο τούβλο ώστε η νέα κατασκευή
να ισορροπεί και αυτή. Αυτό υποδεικνύει
και τον τρόπο λύσης.
Το κέντρο βάρους του 1ου τούβλου απέχει προφανώς
15 cm από την άκρη του. Το σηκώνουμε και
τοποθετούμε από κάτω το επόμενο τούβλο ώστε
το κέντρο βάρους του από πάνω τούβλου
να είναι ακριβώς πάνω από την άκρη του
από κάτω τούβλου. Σηκώνουμε αυτή την
κατασκευή και τοποθετούμε το νέο τούβλο
από κάτω ώστε το κέντρο βάρους της να
είναι στην άκρη του νέου τούβλου.
Φροντίζουμε πάντα να τοποθετούμε τη
δεξιά άκρη του νέου τούβλου κάτω από το
κέντρο βάρους της παλιάς κατασκευής.
Με απλές πράξεις που εμπλέκουν το

κέντρο βάρους διαπιστώνει κανείς ότι
η κατακόρυφη προβολή αυτής της
κατασκευής φτάνει σε απόσταση
το οποίο μπορεί να γίνει όσο μεγάλο θέλουμε
αφού η συγκεκριμένη σειρά αποκλίνει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 12 Αυγούστου, 2008 @ 11:57 μμ
Αυτό που ζητώ σε αυτό το πρόβλημα είναι ένα διαισθητικό επιχείρημα, χωρίς πράξεις, και νομίζω ότι οι υποδείξεις που δίνω παραπάνω μπορούν να βοηθήσουν να βρεθεί κάτι τέτοιο.
Ο συνηθισμένος τρόπος να λύσει κανείς αυτό το πρόβλημα είναι αυτός που περιγράφεις, αλλά αυτή η λύση απαιτεί υπολογισμούς, και σίγουρα δεν είναι φανερό από πού προκύπτει η σειρά που δίνεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 13 Αυγούστου, 2008 @ 12:42 πμ
Από τα ωραία προβλήματα που υπάρχουν σ’αυτή τη σελίδα,αυτό είναι το ωραιότερο! Ή πιο σωστά, με εξιτάρει περισσότερο από τα υπόλοιπα.
Εξηγούμαι για να μην παρεξηγηθώ.
Ωραιότερο μεταξύ αυτών που δύναμαι να καταλάβω δηλαδή. Υποθέτω ότι όλα τα προβλήματά σας είναι ωραία, για όσους μπορούν να τα καταλάβουν άρα και να τα αντιμετωπίσουν. 🙂
Ωραιότερο, γιατί μας αφήνει περιορισμένα «εργαλεία» (πάντως, «χωρίς πράξεις» είπες, έτσι; Όχι χωρίς τύπους. )
Ωραιότερο, γιατί .απότι διάβασα στο άλλο ωραίο θέμα με το στερεό εκ περιστροφής από το Kelvin-Stokes , έχεις σε «εκτίμηση» της διαισθητικές/μπακάλικες λύσεις (σχεδόν μεταφυσικές..) των μηχανικών 🙂
Τέλος, φαντάζομαι ότι η νεκρανάσταση προβλήματος μετά από 5 χρόνια και κάτι μήνες πρέπει να αποτελεί κάποιου είδους ρεκόρ! (τουλάχιστον για το ιστολόγιο) που ήδη έχω κατακτήσει! 🙂
Πάω τώρα (επιτέλους!) στην ουσία.
Τα παρακάτω ισχύουν για όλα τα τούβλα (συμβατικές οπτοπλινθοδομές τουλάχιστον με θεωρητική ομογένεια,δηλαδή σταθερή ,ενιαία καθ’όλον τον όγκο πυκνότητα και σταθερό πλάτος και ύψος )
Καταρχάς, υποθέτω -δεν διευκρινίζεται στην εκφώνηση- ότι η στοίβαξη των τούβλων γίνεται «2-διάστατα» ,δηλαδή με ακρίβεια κατά πλάτος αλφαδιάζονται ,άρα το πρόβλημα είναι στατικής επάρκειας(οριακής) στο επίπεδο ,ας πούμε το καρτεσιανό x-y του χαρτιού/οθόνης.
Η στήλη μπορεί επίσης να επεκτείνεται προς τη ίδια μεριά συνεχώς ή και να εναλλάσσονται οι μεριές όσο ανεβαίνουμε στο ύψος της στήλης.
«Φυσικά» επιχειρηματολογώντας λοιπόν, μπορώ να διαβεβαιώσω ως δομοστατικός (εγγύηση για σεισμό 9 Ρίχτερ πάντως ,σαν κάτι «συναδέλφους», δεν δίνω!) ότι η αναγκαία συνθήκη για να ισορροπεί μια τυχαία στήλη είναι η συνισταμένη των βαρών , δηλαδή η κατακόρυφος που περνάει από το κέντρο μάζας ΟΛΩΝ των τούβλων που βρίσκονται πάνω από ένα (ΟΠΟΙΟΔΗΠΟΤΕ) τούβλο-«βάση» να περνάει/τέμνει (έστω οριακά, με την μαθηματική έννοια του ορίου) αυτό το τούβλο-βάση. Κι αυτό φυσικά ,πρέπει να συμβαίνει διά κάθε τούβλο που ανήκει στη στήλη. Το γιατί η παραπάνω συνθήκη όμως είναι και ικανή ,γιατί δηλαδή να ικανοποιείται για κάθε τούβλο και το σύνολο των υπερτούβλων, είναι το ζητούμενο. «Χωρίς πράξεις» το καλύτερο που μπορώ να σκεφτώ και με βάση και τα hints του Μιχάλη Κολουντζάκη είναι το εξής
Η θέση του κέντρου μάζας κάθε τούβλου μπορεί να υπολογιστεί από τη σχέση
(xA + xΔ)/2 ,όπου χΑ και xΔ οι συντεταγμενες του Α(ριστερού) και Δ(εξιού) άκρου του τούβλου αντίστοιχα. Η θέση του κέντρου μάζας μιας ολόκληρης (οποιασδήποτε και οσοδήποτε μεγάλης/ψηλής!)στήλης είναι η μέση τιμή xi(αριθμητικός μέσος) των θέσεων των κέντρων μάζας όλων των τούβλών. Αν κάνουμε μικρή, πολλή μικρή την μετατόπιση κάθε προσθετου τούβλου μπορούμε να πετύχουμε (μαθηματικώς τουλάχιστον) οσοδήποτε μικρές μετατοπίσεις στον κεντροβαρική συνθήκη ισορροπίας . Μπορούμε να βρούμε δηλαδή τιμή της xi πάντα, οριακά έστω ανάμεσα στα xΑ(ν) και xΔ(ν), οπότε η αναγκαία συνθήκη ,αφού η «συνάρτηση» αυτή είναι «συνεχής» ,πληρείται πάντα ,για οσοδήποτε μεγάλο αριθμό τούβλων ν.
Δεν επιτρέπεονται πράξεις, αλλά μπορούμε να βρούμε το πόσο μπορεί να «ταξιδέψει» από τον άξονα συμμετρίας του αρχικού/1ου τούβλου η άκρη της στήλης μας,αναλόγων των τούβλων που έχουμε. Για ν τούβλα , η «προέκταση» αυτη του άκρου δίνεται από τη σχέση : (1/2)*(1+1/2 + 1/3 +…+1/ν).
Η αρμονική σειρά συγλίνει ΠΟΛΥ αργά, αλλά συγκλίνει! Μόνο που θέλουμε ΠΟΛΛΑ-ΠΟΛΛΑ τούβλα για να φτάσουμε μακριά.
Αν έχω κάνει σωστούς υπολογισμούς , για να εξέχει η άκρη απόσταση ίση με 3 μέτρα (μήκος 10 τούβλων) απαιτούνται περίπου 273.000.000 τούβλα!
Για απόσταση ίση με 15 μέτρα (50 τούβλα) απαιτούνται 1,5 * 10^44 τούβλα!!
Οπότε στα 100 μέτρα , φτάνουμε μεν και ΔΕΝ φτάνουμε δε. Θα θέλαμε αριθμό τούβλων που θα ήταν υπερπολλαπλάσιο πολάκις του εικαζόμενου αριθμού στοιχειωδών σωματιδίων στο σύμπαν (αν αποφασίσουν και καταλήξουν ποτέ οι Φυσικοί, ποια είναι αυτά τα σωματίδια και πόσα είναι αυτά τα Σύμπαντα , κι αν είναι άπειρα ή πεπερασμένα ,κβαντικά ή…ακβάντιστα…) 😆
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 19 Νοεμβρίου, 2013 @ 9:41 μμ
Όλα καλά μέχρι το «Αν κάνουμε μικρή, πολλή μικρή την μετατόπιση κάθε προσθετου τούβλου μπορούμε να πετύχουμε (μαθηματικώς τουλάχιστον) οσοδήποτε μικρές μετατοπίσεις στον κεντροβαρική συνθήκη ισορροπίας«. Αυτό δεν το κατάλαβα όπως δεν κατάλαβα και το αν φτιάχνεις τη στήλη σου χρησιμοποιώντας μια προηγούμενη (όπως λέω στην υπόδειξή μου) ή με κάποιο άλλο τρόπο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Νοεμβρίου, 2013 @ 11:01 μμ
Επίτρεψέ μου να ξεκαθαρίσω κάποια πράγματα. Ουσιαστικά , στο σχόλιό μου δεν είπα κάτι διαφορετικό από τον σχολιαστή xatzial. Δεν μπορώ να προσδιορίσω τι είδους «φυσική»/διαισθητική εξήγηση ζητάς, πάντως τα εισαγωγικά στο «φυσική» τα έχεις βάλει πολύ σωστά,καθότι σίγουρα είναι ένα θέμα στο οποίο το μαθηματικό συμπέρασμα ,δηλαδή η επ’άπειρον ικανότητα να έχουμε «κρέμαση» (απόκλιση του ακραίου πάνω τούβλου από την κατακόρυφο του άκρου του 1ου τούβλου-βάση ) οσοδήποτε μεγάλη, έρχεται σε αντίθεση με τη «φυσική» διαίσθηση του «μέσου» ανθρώπου. (ομολογώ ότι δεν πολυσυμπαθώ την ιδεατή στατιστική έννοια του «μέσου» ανθρώπου,κυρίως επειδή ερμηνεύεται αιθαίρετα από «πονηρούς» η ημιμαθείς που περιβάλλουν την υστεροβουλία ή την ημιμάθειά τους με μαθηματικό «κύρος», αλλά δεν μου έρχεται πιο δόκιμος όρος). Θα έλεγα , με βάση ασφαλώς την προσωπική μου εμπειρία όχι από το συγκεκριμένο θέμα αλλά απο άλλα παρεμφερούς φύσης, ότι αν θέσεις το προβλημα σε κάποιον χωρίς εξειδικευμένη -κάποιου είδους και ποιότητας- τεχνική ή μαθηματική εκπαίδευση θα απαντούσε μάλλον ότι δεν γίνεται να πετύχεις μήκος κρέμασης στο οποίο το τελευταίο πάνω τούβλο θα προεξέχει της βάσης. Αν κάποιος έχει κάποια τεχνική γνώση θα απαντούσε ότι μπορείς να κερδίσεις κάποια «μήκη» τούβλου σε κρέμαση. Νομίζω ότι πολλοί λίγοι θα απαντούσαν διαισθητικά ότι η κρέμαση μπορεί να φτάσει στα 10 (ή 100) μέτρα, πόσω μάλλον στο «άπειρο».
Και αυτό είναι δικαιολογημένο! To μαθηματικό μας μοντέλο είναι καθαρά μαθηματικό-ιδεατό και πολύ μικρή σχέση έχει με την πραγματικότητα. Προυποθέτει: απόλυτα ακριβείς γεωμετρικές διαστάσεις και επιπεδότητα, απόλυτη ομογένεια υλικού άρα και απολυτα ομοιομορφη κατανομή φορτίου «ιδίου βάρους» στα τούβλα. Πρέπει επίσης τα τούβλα και το «τραπέζι»/βάση στήριξης να είναι απείρως άκαμπτα (rigid) ,δηλαδή να έχουν μηχανικές ιδιότητες και αντοχές που δεν μπορέι να υπάρξουν. Επίσης το μαθηματικό μοντέλο προυποθέτει απουσία τριβής,καθότι η παραμικρή τριβή θα άλλαζε τις εξισώσεις ισσοροπίας αφού θα επεισέρχονταν και οριζόντιες δυνάμεις. Eπίσης, ακόμη και πάχους τρσιγαρόχαρτου να ήταν τα τούβλα ,το ύψος που φτάνει η στήλη για μεγάλους αριθμούς τούβλων άρα και κρέμασης θα σήμαινε μεταβολόμενες βαρυτικές δυνάμεις ,χωρίς να λαμβάνουμε υπ’όψι καθόλου τις δυνάμεις λόγω κινήσεως της Γης, Coriolis κ.λ.π. Εν ολίγοις, «φυσικό» μοντέλο που να πλησιάζει έστω το μαθηματικό, δεν μπορέι να υπάρξει ούτε κατά προσέγγιση.
Με προβληματίζει επίσης αυτό που λες στο hint για τον ελέφαντα, αν το έχω ερμηνέψει σωστά. Το πρόβλημα -μιλάω εφεξής για το καθαρά μαθηματικό μοντέλο!- δεν είναι πρόβλημα δυνάμεων /καθέτων βαρυτικών συνιστωσών , αλλά πρόβλημα ροπών. Ουτε πρέπει να συγχέουμε τη στοιβαρότητα με την ευστάθεια (stability ,Stabilitaet) . Άλλο πράγμα επίσης η στατική ευστάθεια και ο «βαθμός» της (degree of static indifference) και άλλο πράγμα η ισορροπία(Αλγεβρικό άθροισμα δυνάμεων ΣFi(x,y)και ροπών ΣΜi σε ένα οποιοδήποτε σημείο i της κατασκευής που πρέπει να είναι 0, για να είναι το σύστημα ισοστατικό). Όταν δηλαδή ο ελέφαντας είναι σούζα και στηρίζεται στο νύχι του ,το φτερό παίζει ρόλο.
Για να αποσαφηνίσω λίγο τα παραπάνω και να εξηγήσω γιατί το θέμα αντιμετωπίζεται από «πάνω προς τα κάτω» κι όχι ανάποδα θα χρησιμοποιήσω ένα παράδειγμα. Αν στοιβάξουμε απολύτως κεντρικά , δηλαδή τα κέντρα μάζας να δημιουργούν μια κατακόρυφο, ν τούβλα, και πάνω τους βάλουμε το τελευταίο με κρέμαση > 1/2* μήκος τούβλου ,προφανώς το τούβλο καταρέει ,αλλά το συσσωμάτωμα {στοιβας ν τουβλων + ενός τούβλου} προφανώς «ισορροπεί» αν θεωρηθεί εννιαίο ως προς το κάτω επίπεδο αναφοράς -στήριξης. Το κέντρο μάζας του συσσωματώματος μετατοπίστηκε απλώς απειροελάχιστα προς τα αριστερά (ή δεξιά).
Μιας και είμαστε μαθηματικό ιστολόγιο , δεν είναι δόκιμο να κάνω διάλεξη Στατικής , ουτε είναι βέβια και αυτό το ζητούμενο, αλλά προσπαθώντας να πιάσω το «σφυγμο» που ζητάς, το καλύτερο «διαισθητικο-φυσικό» που μπορώ να παράξω είναι μάλλον το εξής:
Όπως προείπα στο άλλο σχόλιο η μέγιστη (θεωρητική πάντα) δυνατή «κεντροβαρική κρέμαση» (δηλαδή η απόκλιση των εκάστοτε βαρυκέντρων offset), ας την ονομάσω Κ για μονόμπαντη (προς την ίδια μεριά) στοίβαξη ν τούβλων είναι:
Κν=1/2 + 1/4 + 1/6 + 1/8 +….+ 1/2ν («μήκη» τουβλου ,εννοειται) (1)
Aν αποδειχτεί αυτό ,τελειώσαμε.
Σκέφτομαι με Επαγωγή.
Για ν=1 (το αρχικό πάνω τούβλο) το κέντρο μάζας απέχει 1/2*L από το άκρο του τούβλου. Άρα κρέμαση (offset) = 1/2 και η (1) είναι αληθής για το Κ1.
Για ν >ή ίσο 2, υποθέτουμε ότι Κ(ν-1) αληθεύει ώστε να αποδείξουμε Κν=αληθής
Μία οποιαδήποτε στοίβα από ν τούβλα αποτελείται από μια «υποστοίβα» 1 (ενός) τούβλου και μία «υπερστοίβα»(υπερκατασκευή) από ν-1 τούβλα.
Για να πετύχουμε την μέγιστη δυνατή κρέμαση με ν τούβλα ,τα υπερκείμενα ν-1 τούβλα πρέπει να έχουν κι αυτά τη μέγιστη δυνατή κρέμαση Κ(ν-1). Αν δεν ίσχυε αυτό θα μπορούσαμε να αλλάξουμε την υπερστοίβα ν-1 με μια άλλη που θα είχε μεγαλύτερη κρέμαση. Επιπροσθέτως, το βαρύκεντρο της υπερστοίβας (ν-1) πρέπει να κείται ΑΚΡΙΒΩΣ πάνω από την δεξιά άκρη του κάτω τούβλου (υποθέτω στοίβαξη καθ’ύψος «προς τα δεξιά») ώστε να έχουμε οριακή ισορροπία. Αν δεν ίσχυε αυτό, αν είχαμε δηλαδή κάποιον «αέρα» περιθώριο στην κατακόρυφο, θα μπορούσαμε απλά να σπρώξουμε (shift) λίγο την υπερστοίβα των ν-1 προς τα δεξιά, πάλι άτοπο.
Ετσι, έχουμε περιγράψει επακριβώς την γεωμετρία των κρεμάσεων για στοίβα ν τούβλων. Το κ.β της υπερστοίβας απέχει Κ(ν-1) από το δεξί ακροτελέυτειο σημείο της όλης κατασκευής, και το κ.β της βάσης-τούβλου απέχει Κ(ν-1)+1/2
Πρέπει εδώ να ανφερθεί ότι όταν δύο σώματα μάζας m1 και m2 αντίστοιχα έχουν κέντρα μάζας σε θέσεις/συντεταγ. x1 και x2 αντίστοιχα, το κέντρο βάρους του συσσωματώματος (m1ένωση m2) βρίσκεται στη θέση: (x1m1+x2m2)/(m1+m2) . (για να πληρείται η συνθήκη άθροισμα ροπών Μy (y κάθετος στο χαρτί άξονα) =0)
Άρα με βάση αυτό και τα προαναφερθέντα , η μέγιθστη δυνατή κ.β. κρέμαση είναι:
Kν = [Κ(ν-1) * (ν-1) + (Κ(ν-1) + 1/2)*1] /(ν-1+1)
ή Κν=Κ(ν-1) +1/2ν = 1/2 + 1/4 + 1/6 +…+1/2ν
Ο.Ε.Δ.
Τώρα, η αρμονική σειρά ,είτε τη φράξουμε «στο περίπου» ,μεταξύ του ν-ιοστού αρμονικού άθροισματος
Ην= ln(ν+1) και του 1+ln(ν), είτε με την ολοκληρ. μέθοδο Όυλερ-Μακλώριν και βάλουμε και τη σταθερά Όυλερ-Μασκερόνι γ στο «παιχνίδι» , δεν αλλάζει κάτι επί της ουσίας.
Η μέγιστη δυνατή κρέμαση (κανονική πλέον! όχι η κεντροβρική) ανά τούβλο -από πάνω προς τα κάτω- είναι : Για 1 τούβλο 1/2 *Η1=1/2
Για 2 τ. 1/2 * Η2= (1/2)*(1+1/2)= 3/4
Για 3 τ. 1/2Η3 =11/12
Για 4 τ. 1/2Η4 = 1/2(1+1/2+1/3+1/4)= 25/24 (μόλις περάσμαε το «μήκος τούβλου»
κ.λ.π.
Αντιλαμβάνομαι ότι η μαθηματική επαγωγή , δεν είναι και ό,τι πιο «φυσικό» και διαισθητικό, αλλά δεν μπορώ να σκεφτώ κάποιο άλλο επιχείρημα, και περιμένω με ενδιαφέρον να ακούσω την τυχόν διαφορετική σου άποψη Μιχάλη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 20 Νοεμβρίου, 2013 @ 5:17 μμ
Ίσως είναι καιρός να πω τι ακριβώς περίμενα.
Όπως λέω και στην πρώτη μου υπόδειξη αρκεί να δείξω ένα τρόπο για να πάω από μια στήλη Σ με προβολή (κατακόρυφη στο οριζόντιο επίπεδο) μήκους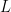 σε μια νέα στήλη Τ με προβολή
σε μια νέα στήλη Τ με προβολή  (όλα τα μήκη σε εκατοστά με το ένα τούβλο να έχει μήκος 30 όπως στην εκφώνηση).
(όλα τα μήκη σε εκατοστά με το ένα τούβλο να έχει μήκος 30 όπως στην εκφώνηση).
Πώς θα χρησιμοποιήσουμε λοιπόν τη στήλη Σ για να φτιάξουμε τη νέα στήλη Τ που πάει 1 εκατ. πιο μακριά;
Για να είναι η περιγραφή πιο καθαρή ας υποθέσουμε ότι ο σωρός μας με τα τούβλα πατάει πάνω σ’ένα τραπέζι και ο σκοπός μας είναι να τον κάνουμε να πάει όσο μπορούμε πιο μακριά προς τα δεξιά. Το τραπέζι το θεωρούμε σταθερό και ακλόνητο. Ας είναι η δεξιά άκρη του τραπεζιού πάνω από την τετμημένη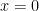 .
.
Έχουμε λοιπόν το σωρό Σ που πατάει πάνω στο τραπέζι και αν προβληθεί κάτω φτάνει μέχρι και την τετμημένη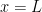 . Παραμερίζουμε προσωρινά αυτό το σωρό και φτιάχνουμε ένα άλλο, τελείως κατακόρυφο, σωρό Κ ο οποίος (α) εξέχει από το τραπέζι κατά 1 εκατ. προς τα δεξιά και (β) έχει N τούβλα, το ένα ακριβώς πάνω από το άλλο, όπου ο αριθμός N είναι τεράστιος και εξαρτάται από το πόσα τούβλα υπάρχουν στον (παραμερισμένο) σωρό Σ.
. Παραμερίζουμε προσωρινά αυτό το σωρό και φτιάχνουμε ένα άλλο, τελείως κατακόρυφο, σωρό Κ ο οποίος (α) εξέχει από το τραπέζι κατά 1 εκατ. προς τα δεξιά και (β) έχει N τούβλα, το ένα ακριβώς πάνω από το άλλο, όπου ο αριθμός N είναι τεράστιος και εξαρτάται από το πόσα τούβλα υπάρχουν στον (παραμερισμένο) σωρό Σ.
Ο σωρός αυτός Κ προφανώς ισορροπεί και δεν πέφτει. Σηκώνουμε τώρα τον σωρό Σ και τον τοποθετούμε πάνω στο σωρό Κ ωσάν το κορυφαίο τούβλο του Κ να είναι η επιφάνεια του τραπεζιού. Το κλειδί στο επιχείρημα είναι ότι αν ο αριθμός N είναι αρκετά μεγάλος τότε ο σωρός Κ ούτε καν θα αισθανθεί το νέο βάρος που του βάλαμε από πάνω (ο ελέφαντας είναι ο Κ, το φτερό είναι το Σ) και θα εξακολουθήσει να ισορροπεί. Ο νέος μας συνολικός σωρός Σ’ τώρα, που αποτελείται από τον Κ κι από πάνω του τον Σ, αν προβληθεί κάτω φτάνει στην τετμημένη , όπως έπρεπε να αποδείξουμε.
, όπως έπρεπε να αποδείξουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Νοεμβρίου, 2013 @ 12:55 πμ
Α ,μάλιστα! Εξαιρετικό επαγωγικό επιχείρημα Μιχάλη!
Το κάπως ειρωνικό (για μένα) είναι ότι έφτασα πολύ κοντά του στο τελευταίο μου σχόλιο, όπου χρησιμοποίησα όπως είδες ακριβώς αυτόν τον «υπερσωρό»-στήριξης Ν ,αλλά για τον «λάθος» σκοπό!, δηλαδή για να δείξω ότι δεν αρκεί σαν επιχείρημα ευστάθειας η συγκριτική μεταξύ δύο τυχαίων συσσωματώσεων κεντροβαρική «ικανή» συνθήκη. Αν ειχα «ξεκολλήσει» στο σημείο εκείνο…δηλαδή αν έσπρωχνα λίγο-έως πολύ, το πάνω παλιότουβλο προς τ’αριστερά…αν..(γιαγιάδες,καρούλια,κ.λ.π… 🙂
Mια διαισθητική επαγωγή λοιπόν, που θεμελιώνει ένα θεώρημα «ύπαρξης» και μόνο, δεν λέει τίποτε για το όριο του αριθμού τούβλων ανά K(n) (ή L(n) όπως το ονόμασες) ή την μάξιμουμ δυνατή κατανομή, (αλλά δεν ήταν αυτό το ζητούμενο!) και πανίσχυρο αναμφισβήτητα λογικά, μιας και δεν υπάρχει άνω φράγμα στους φυσικούς αριθμούς, άρα και στο μέγεθος των διαδοχικών μας «ελεφάντων» και αναμφισβήτητα αποδεικνύει την δυνατότητα απειρίας της κρέμασης.
Συγχαρητήρια για την ιδέα, και σ’ευχαριστώ για το ωραίο θέμα και την εποικοδομητική συζήτηση! 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 21 Νοεμβρίου, 2013 @ 1:51 πμ
Κι εγώ ευχαριστώ για την ενεργή συμμετοχή.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Νοεμβρίου, 2013 @ 1:52 πμ