Έστω ένα σύνολο θετικού μέτρου. Δείξτε ότι υπάρχει πραγματική, μετρήσιμη συνάρτηση
τέτοια ώστε
.
25 Δεκεμβρίου, 2008
Άπειρο ολοκλήρωμα
5 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Έστω ένα σύνολο θετικού μέτρου. Δείξτε ότι υπάρχει πραγματική, μετρήσιμη συνάρτηση
τέτοια ώστε
.
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.
Καλημέρα και χρόνια πολλά σε όλους! Ας κάνω μια απόπειρα: Εφόσον το έχει θετικό μέτρο, σχεδόν κάθε σημείο του είναι σημείο πυκνότητας αυτού. Έστω
έχει θετικό μέτρο, σχεδόν κάθε σημείο του είναι σημείο πυκνότητας αυτού. Έστω 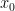 ένα τέτοιο σημείο. Τότε, η συνάρτηση
ένα τέτοιο σημείο. Τότε, η συνάρτηση  με
με  αν
αν 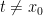 και
και  αλλιώς, έχει
αλλιώς, έχει 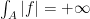 . Διαφορετικά, για
. Διαφορετικά, για  αρκετά μικρό θα είχαμε
αρκετά μικρό θα είχαμε  και έχουμε αντίφαση.
και έχουμε αντίφαση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από petvalet — 27 Δεκεμβρίου, 2008 @ 12:21 μμ
Πολύ σωστά.
 , καθώς
, καθώς 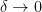 . Απ’την άλλη
. Απ’την άλλη
Για όσους δεν βλέπουν την αντίφαση, αν το ολοκλήρωμα ήταν πεπερασμένο, τότε θα είχαμε
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 27 Δεκεμβρίου, 2008 @ 7:25 μμ
Και, χωρίς το θεώρημα του Lebesgue (ύπαρξη σημείων πυκνότητας); Είναι σχετικά βαρύ θεώρημα γι’ αυτή την άσκηση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Δεκεμβρίου, 2008 @ 8:03 μμ
Χρονια πολλα!
Θα προσπαθησω να δωσω μια αποδειξη που δε χρησιμοποιει το θεωρημα Lebesgue. Βασιζεται ουσιαστικα στην ιδια ιδεα με αυτη του petvalet.
Κατ’αρχας, μπορουμε να υποθεσουμε οτι![A\subset[0,1]](https://s0.wp.com/latex.php?latex=A%5Csubset%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Αν δεν ισχυει αυτο, τοτε μπορουμε να βρουμε διαστημα
. Αν δεν ισχυει αυτο, τοτε μπορουμε να βρουμε διαστημα 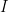 τετοιο ωστε
τετοιο ωστε  , να μετεφερουμε το
, να μετεφερουμε το  στο [0,1] και να δουλεψουμε εκει.
στο [0,1] και να δουλεψουμε εκει.
Θα ορισουμε επαγωγικα μια ακολουθια διαστηματων . Θετουμε
. Θετουμε ![I_0=[0,1]](https://s0.wp.com/latex.php?latex=I_0%3D%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Διαιρουμε το
. Διαιρουμε το  σε δυο ισα υποδιαστηματα και καλουμε
σε δυο ισα υποδιαστηματα και καλουμε  αυτο το διαστημα για το οποιο
αυτο το διαστημα για το οποιο  (αν αυτο ισχυει και για τα δυο υποδιαστηματα, τοτε διαλεγουμε ενα στην τυχη). Επειτα διαιρουμε στα δυο το
(αν αυτο ισχυει και για τα δυο υποδιαστηματα, τοτε διαλεγουμε ενα στην τυχη). Επειτα διαιρουμε στα δυο το  και καλουμε
και καλουμε 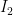 αυτο το διαστημα για το οποιο
αυτο το διαστημα για το οποιο 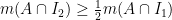 και ουτω καθ’εξης. Απο την κατασκευη θα εχουμε οτι
και ουτω καθ’εξης. Απο την κατασκευη θα εχουμε οτι
Τωρα θετουμε
Η ειναι πεπερασμενη παντου εκτος ισως απο ενα σημειο, την τομη των διαστηματων
ειναι πεπερασμενη παντου εκτος ισως απο ενα σημειο, την τομη των διαστηματων 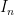 (και μπορουμε να την τροποιησουμε σε αυτο). Θα εχουμε τοτε για αυτη τη συναρτηση οτι
(και μπορουμε να την τροποιησουμε σε αυτο). Θα εχουμε τοτε για αυτη τη συναρτηση οτι
το οποιο ειναι ατοπο, οπως ειδαμε και στα προηγουμενα σχολια.
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 30 Δεκεμβρίου, 2008 @ 2:16 μμ
Σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 30 Δεκεμβρίου, 2008 @ 8:51 μμ