Τρεις πόλεις είναι χτισμένες στη στέπα και η κυβέρνηση της χώρας αποφάσισε επιτέλους να φτιάξει ένα αεροδρόμιο που να τις εξυπηρετεί. Οι πόλεις θα συνδεθούν με το αεροδρόμιο με αυτοκινητοδρόμους. Οι δρόμοι όμως κοστίζουν και η κυβέρνηση χρήματα πολλά δεν θέλει να διαθέσει. Σας προσλαμβάνει λοιπόν για να γνωμοδοτήσετε που πρέπει να χτιστεί το αεροδρόμιο ώστε το κόστος κατασκευής των τριών αυτοκινητοδρόμων να είναι ελάχιστο. Μάλιστα, το μόνο που προτίθεται να σας δώσει είναι ένας χάρτης της περιοχής, ένας κανόνας κι ένας διαβήτης. Πώς θα υποδείξετε το καταλληλότερο σημείο;
26 Οκτωβρίου, 2008
24 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Προβλήματα Μαθηματικών 
Αυτό που θέλουμε να βρούμε είναι το σημείο του επιπέδου για το οποίο ελαχιστοποιείται το άθροισμα των αποστάσεων του από τις τρεις πόλεις. Δείξτε ότι το σημείο αυτό, αν δεν είναι μια από τις πόλεις, τότε βλέπει τα ευθύγραμμα τμήματα που συνδέουν τις πόλεις υπό γωνία 120 μοιρών.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 31 Οκτωβρίου, 2008 @ 12:17 μμ
Το βαρύκεντρο δηλαδή του τριγώνου που σχηματίζεται από τις τρεις πόλεις..
Μου αρέσει!Μου αρέσει!
Σχόλιο από maximin — 1 Νοεμβρίου, 2008 @ 3:41 πμ
Όχι maximin. Το βαρύκεντρο ενός τριγώνου δεν έχει αυτή την ιδιότητα (παρά μόνο αν το τρίγωνο είναι ισόπλευρο.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 1 Νοεμβρίου, 2008 @ 5:07 πμ
Μια ερώτηση,γιατί δεν θυμάμαι από άλγεβρα.. συν(α+β) μπορεί να αναλυθεί με κάποιο τύπο σε συνα,συνβ ;
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 24 Ιανουαρίου, 2009 @ 8:41 μμ
Υπάρχει, δοκίμασε να βάλεις cosine στη wikipedia.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 24 Ιανουαρίου, 2009 @ 9:28 μμ
talsfan:
Το κόλπο γι’ αυτές τις ταυτότητες είναι να θυμάσαι μόνο μία: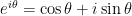
. Όλες οι άλλες βγαίνουν με απλές πράξεις. Π.χ., για να βρείς την ταυτότητα για το 
κάνεις το εξής:
Τέλος εξισώνεις πραγματικά και φανταστικά μέρη και παίρνεις τις ταυτότητες για
και 
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 24 Ιανουαρίου, 2009 @ 9:49 μμ
Α,ευχαριστώ, είναι σίγουρα χρήσιμο αυτό το κόλπο για τα ημίτονα, συνημίτονα.
Έκανα μια προσπάθεια, αν και φοβάμαι δεν είναι σωστή η λύση που δίνω. Παρόλα αυτά, ας την εκθέσω.
Έστω ότι οι πόλεις αυτές συμβολίζονται ως Α,Β,Γ σημεία στο καρτεσιανό επίπεδο. (άρα στο τρίγωνο ΑΒΓ: ΒΓ=α, ΑΓ=β, ΑΒ=γ ). Έστω και ότι το προβλεπόμενο αεροδρόμιο συμβολίζεται με ένα σημείο Δ και τέλος, έστω ΑΔ=δ1, ΒΔ=δ2, ΓΔ=δ3.
Θέλουμε να ελαχιστοποιήσουμε το άθροισμα δ1+δ2+δ3.
Από το νόμο των συνημιτόνων στο τρίγωνο ΑΔΒ, για τη γωνία ΑΔΒ, είναι:
γ^2= δ1^2 + δ2^2 – 2(δ1)(δ2)συνΑΔΒ. Τη σχέση αυτή την έλυσα ως προς δ1 και απέρριψα τη μία λύση από τη δευτεροβάθμια. Συγκεκριμένα, οι λύσεις που έβγαλα είναι οι (δ2)συνΑΔΒ +- ρίζα(γ^2 – (δ2)^2*ημ^2(ΑΔΒ) ).
Κράτησα μόνο αυτή με το + ανάμεσα στους δύο όρους, γιατί η άλλη, για να είναι θετική ( αφού εκφράζει το δ1 μήκος ) θα πρέπει δ2>γ άτοπο, γιατί τότε το Δ θα ήταν εκτός του τριγώνου ΑΒΓ.
Έκανα στη συνέχεια το ίδιο για να εκφράσω το δ3 συναρτήσει του δ2. ( νόμο συνημιτόνων στο τρίγωνο ΒΔΓ και λύση ως προς δ3 ).
Μετά πήρα το άθροισμα δ1+δ2+δ3, έκανα αντικατάσταση στα δ1,δ3 και έβγαλα ότι:
δ1+δ2+δ3 = (δ2)(1 + συνΑΔΒ + συνΒΔΓ) + ρίζα(γ^2 – (δ2)^2*ημ^2(ΑΔΒ) ) + ρίζα(…)
Μηδενισμός του (δ2)(1 + συνΑΔΒ + συνΒΔΓ) γίνεται για γωνίες ΑΔΒ=ΒΔΓ=120 ή για Α,Δ,Β συνευθειακά ή Β,Δ,Γ συνευθειακά ( οπότε το Δ είναι κορυφή του τριγώνου ΑΒΓ ).
Ελπίζω να μην έγινα πολύ κουραστικός…
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 24 Ιανουαρίου, 2009 @ 11:04 μμ
talsfan:
Υπάρχουν κάποια κενά/λάθη στο συλλογισμό σου:
1. Από που προκύπτει ότι η ελαχιστοποίηση του
προκύπτει όταν μηδενίζεται η παράσταση που γράφεις (
);
2. Η παράσταση αυτή δεν μηδενίζεται μόνο στις περιπτώσεις που γράφεις, oύτε μηδενίζεται πάντα αν τα Α,Δ,Β είναι συνευθειακά (το Γ δεν μπορεί να είναι οπουδήποτε.)
3. Τέλος, στην περίπτωση που η γωνία ΑΒΔ είναι αμβλεία (και άρα και η ΑΒΓ) η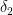
δίνεται από τη ρίζα του τριωνύμου που απορρίπτεις. Αυτό μπορείς να το δεις γιατί το 
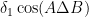είναι η απόσταση του Δ από το ίχνος Η του ύψους από το Α στο τρίγωνο ΑΔΒ, που επειδή η ΑΒΔ είναι αμβλεία θα βρίσκεται στην προέκταση της ΒΔ προς το Β και άρα θα είναι ΔΗ>ΔΒ, δηλαδή 
. Βέβαια αυτό το αναφέρω πιο πολύ για λόγους ακρίβειας αφού τότε μπορείς να εναλλάξεις το ρόλο των 
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 25 Ιανουαρίου, 2009 @ 1:26 πμ
Νέα Υπόδειξη
Φανταστείτε πώς απλώνετε το χάρτη σε ένα τραπέζι και με ένα τρυπάνι τρυπάτε το τραπέζι στα σημεία που βρίσκονται οι πόλεις. Στη συνέχεια περάστε πετονιά μέσα από κάθε τρύπα και δέστε από μια μπάλλα μπιλιάρδου στα άκρα της πετονιάς που βρίσκονται κάτω από το τραπέζι. Τέλος, δέστε τα τρια άκρα πετονιάς που βρίσκονται πάνω από το τραπέζι μεταξύ τους και κρατήστε το σύστημα από εκεί. Μια και όλα αυτά τα φανταζόμαστε, η πετονιά είναι αβαρής και τριβές δεν υπάρχουν. Τι θα συμβεί αν αφήσετε τις μπάλλες που είναι δεμένες με τις πετονιές να κινηθούν;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 25 Ιανουαρίου, 2009 @ 2:49 μμ
Αν ονομάσουμε Δ το σημείο που δένουμε τις πετονιές μεταξύ τους πάνω από το τραπέζι, τότε όταν το σύστημα ισορροπήσει, στο σημείο Δ θα ασκούνται τρεις ίσου μέτρου δυνάμεις F1,F2,F3=F=Β, όπου Β=m*g το βάρος της κάθε μπάλας, m η μάζα της κάθε μπάλας και g η επιτάχυνση της βαρύτητας (αβαρείς πετονιές, δεν υπάρχουν τριβές,άρα μόνο το βάρος της κάθε μπάλας παίζει ρόλο – εκφραζόμενο στο σημείο Δ ως τάση του νήματος ή της πετονιάς ).
Η διεύθυνση των τριών αυτών δυνάμεων θα είναι πάνω στις πετονιές (τμήματα αυτών πάνω από το τραπέζι) από το σημείο Δ προς τις τρύπες που ανοίξαμε στο τραπέζι (έστω Α,Β,Γ). Άρα, έχουμε τρεις δυνάμεις F ίσου μέτρου, διεύθυνσης ΔΑ,ΔΒ,ΔΓ και φοράς από το Δ στο Α, από το Δ στο Β, από το Δ στο Γ (διανύσματα, αφού πρόκειται για δυνάμεις-δηλαδή διανυσματικά μεγέθη).
Οι γωνίες που σχηματίζονται μεταξύ των ΔΑ,ΔΒ,ΔΓ είναι άγνωστες, αλλά αφού το σύστημα ισορροπεί, αν αναλύσουμε τις δυνάμεις σε δυο κατακόρυφους μεταξύ τους άξονες, θα καταλήξουμε ότι οι γωνίες ΑΔΒ, ΑΔΓ, ΒΔΓ είναι ίσες μεταξύ τους (=120) (επειδή οι δυνάμεις αυτές έχουν ίσα μέτρα).
Οι δυνάμεις αυτές – το βάρος,δηλαδή των μπαλών- τείνουν να μειώσουν όσο γίνεται (λόγω βαρύτητας προφανώς) το άθροισμα μήκους των τμημάτων ΔΑ,ΔΒ,ΔΓ (αφού η πετονιά που βρίσκεται πανω από το τραπέζι τεντώνεται). Άρα, ΔΑ+ΔΒ+ΔΓ ελάχιστο όταν οι μεταξύ τους γωνίες είναι ίσες (=120).
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 25 Ιανουαρίου, 2009 @ 4:15 μμ
Περίπου… Το άθροισμα των αποστάσεων ελαχιστοποιείται γιατί το σύστημα θα ισορροπήσει εκεί που η δυναμική του ενέργεια είναι ελάχιστη, δηλαδή εκεί που το άθροισμα του ύψους των σφαιρών από το έδαφος είναι ελάχιστο. Επειδή όμως το μήκος των κομματιών πετονιάς είναι σταθερό, αυτό γίνεται όταν το άθροισμα των μηκών της πετονιάς πάνω στο τραπέζι είναι ελάχιστο. Είναι έτσι; Σχεδόν. Αρκεί το σημείο που έχουμε δέσει τις τρεις πετονιές μεταξύ τους να μην πέσει μέσα σε μια από τις τρύπες! Σ’ αυτήν την περίπτωση το σημείο που ελαχιστοποιεί το άθροισμα των αποστάσεων είναι μια από τις κορυφές του τριγώνου.
Το γεγονός ότι αν τρεις δυνάμεις ίσου μέτρου ισορροπούν τότε σχηματίζουν μεταξύ τους γωνία 120 μοιρών το έχουμε δει και σε προηγούμενο post.
Μένει τώρα να βρείτε πότε το ελάχιστο άθροισμα επιτυγχάνεται στο εσωτερικό του τριγώνου, οπότε όπως είπε ο talsfan θα βλέπει τις πλευρές του τριγώνου υπό γωνία 120 μοιρών (και άρα μπορεί να κατασκευαστεί με κανόνα και διαβήτη (πώς;)) και πότε επιτυγχάνεται σε μια από τις κορυφές του τριγώνου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 25 Ιανουαρίου, 2009 @ 10:22 μμ
Φαντάζομαι έχει σχέση με το σε ποιες περιπτώσεις υπάρχει σημείο εσωτερικό του τριγώνου που να βλέπει τις πλευρές του τριγώνου αυτού υπό γωνία 120. Τέτοια σημεία υπάρχουν για τρίγωνα που έχουν γωνίες ΔΒΓ, ΑΓΒ > ΒΓΔ, άρα και ΒΔΓ > ΒΑΓ.
Άρα, τέτοιο σημείο Δ που να είναι εσωτερικό του τριγώνου και να βλέπει υπό γωνία 120 τις πλευρές του τριγώνου μπορεί να υπάρξει μόνο σε τρίγωνα με όλες τις γωνίες 120, το ελάχιστο άθροισμα επιτυγχάνεται σε μια από τις κορφυφές του τριγώνου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 26 Ιανουαρίου, 2009 @ 12:44 πμ
:S Τα εμφάνισε όπως να’ναι…
Τέλος πάντων, για να μην τα γράφω πάλι. Απέδειξα ότι εσωτερικό σημείο Δ που να βλέπει τις πλευρές του τριγώνου υπό γωνία 120 μπορεί να υπάρξει μόνο σε τρίγωνα με όλες τις γωνίες <120. (συνοπτικά είπα ότι φαίνεται ως εξής: προεκτείνουμε την ΑΔ, Μ σημείο τομής με ΒΓ. Μετά από τα τρίγωνα ΒΑΓ, ΒΔΓ και τα αθροίσματα των γωνιών τους φαίνεται ότι ΒΑΓ = 120 ή οποιαδήποτε τέλος πάντων γωνία του τριγώνου ). Επομένως, σε αμβλυγώνια >120, το ζητούμενο σημείο είναι κορυφή του τριγώνου, στα υπόλοιπα εσωτερικό σημείο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 26 Ιανουαρίου, 2009 @ 12:51 πμ
στην παρένθεση:φαίνεται ότι ΒΑΓ>ΒΔΓ άρα δεν μπορεί να είναι η ΒΑΓ ή οποιαδήποτε άλλη γωνία του τριγώνου >120.
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 26 Ιανουαρίου, 2009 @ 1:02 πμ
Πράγματι αν μια γωνία Α του τριγώνου είναι >120 μοίρες, τότε όπως εξηγείς στο σχόλιο 13 όλα τα σημεία στο εσωτερικό (ή στις πλευρές) του τριγώνου θα βλέπουν την απέναντι της Α πλευρά υπό γωνία >Α>120 και άρα σ’ αυτή την περίπτωση το ελάχιστο άθροισμα θα λαμβάνεται στην κορυφή της γωνίας Α (απέναντι από την αμβλεία γωνία Α θα βρίσκεται η μεγαλύτερη πλευρά του τριγώνου.)
Μένει να δείξουμε όμως ότι αν όλες οι γωνίες του τριγώνου είναι μικρότερες από 120 μοίρες τότε υπάρχει σημείο στο εσωτερικό του τριγώνου που βλέπει όλες τις πλευρές υπό γωνία 120 μοιρών και το ελάχιστο λαμβάνεται εκεί.
Και κάτι ακόμη. Αν θέλουμε να είμαστε ακριβείς, το σύστημα θα ισορροπήσει σε ένα σημείο που είναι τοπικό ελάχιστο της δυναμικής ενέργειας (εναλλακτικά του αθροίσματος των αποστάσεων). Γιατί αυτό θα είναι κατ’ ανάγκη και ολικό ελάχιστο;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 27 Ιανουαρίου, 2009 @ 10:44 μμ
Μια ερώτηση.
Έστω τρίγωνο ΑΒΓ, Μ μέσο ΒΓ, ευθεία ε που περνά από το Μ, κάθετη στη ΒΓ. Τότε θα υπάρχει σημείο Κ στη ΒΓ, ώστε η γωνία ΒΚΓ να είναι ορθή ( θα είναι ΜΚ=ΒΓ/2, αφού το το Κ ανήκει στον κύκλο (Μ,ΒΓ/2) ).
Επίσης, θα υπάρχει σημείο Λ μεταξύ Κ,Μ πάνω στην ε, ώστε η γωνία ΒΛΓ= 120. Επειδή Μ μέσο ΒΓ, ε κάθετη στη ΒΓ από κατασκευή, τότε το τρίγωνο ΒΛΓ είναι ισοσκελές με βάση τη ΒΓ, εφόσον ΛΜ είναι και ύψος και διάμεσος, άρα και η γωνία ΛΓΜ=30. Το τρίγωνο ΜΛΓ είναι ορθογώνιο, εφΛΓΜ=ΜΛ/ΜΓ, αρα ΜΛ=ΒΓ(ρίζα3)/2
Είναι σωστό ότι τα σημεία που βλέπουν τη ΒΓ υπό γωνία 120 θα κινούνται στον κύκλο με κέντρο Μ, ακτίνα ΜΛ (εκτός των σημείων τομής του κύκλου αυτού με τη ΒΓ) ;
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 29 Ιανουαρίου, 2009 @ 11:00 μμ
συγγνώμη. Επειδή εφ30 = (ρίζα3)/3, τότε ΜΛ=ΒΓ(ρίζα3)/6.
Μου αρέσει!Μου αρέσει!
Σχόλιο από talsfan — 29 Ιανουαρίου, 2009 @ 11:25 μμ
talsfan:
Δεν είναι σωστό. Θα είναι δύο τόξα κύκλων- ένα σε κάθε ημιεπίπεδο που ορίζει η ευθεία ΒΓ (αυτό μπορείς να το δεις εύκολα από τα κριτήρια για να είναι εγγράψιμο ένα τετράπλευρο) αλλά το κέντρο και η ακτίνα δεν είναι αυτά που λες
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 30 Ιανουαρίου, 2009 @ 7:29 μμ
Με την βοήθεια του διαβήτη σχεδιάζουμε τρία ισόπλευρα τρίγωνα, καθε ένα απο το οποίο εχει σαν βάση μία απο τις πλευρές του τριγώνου που σχηματίζουν οι τρείς πόλεις, και τα οποία κείτονται εκτός του τριγώνου αυτου.
Σχεδιάζοντας τους περιγεγραμμένους κύκλους καθενός από τα τρία ισόπλευρα τρίγωνα, το ζητούμενο σημείο για τη βέλτιστη θέση του αεροδρομίου δίνεται από το σημείο τομής και των τριών κύκλων, το οποίο είναι μοναδικό.
Αυτά στην περίπτωση που το τρίγωνο των τριών πόλεων δεν εχει γωνία μεγαλύτερη ή ίση με 120°. Γιατί αν έχει τέτοια γωνία, τότε η πόλη που βρίσκεται σε αυτή, πρεπει να εχει και το αεροδρόμιο
Μου αρέσει!Μου αρέσει!
Σχόλιο από yioryos — 5 Αυγούστου, 2009 @ 6:52 μμ
Σωστά είναι όλα αυτά που λες yioryos. Μπορείς να μας εξηγήσεις και γιατί οι τρεις κύκλοι συντρέχουν και γιατί το σημείο στο οποίο συντρέχουν είναι το σημείο στο εσωτερικό του τριγώνου που ελαχιστοποιεί το άθροισμα των αποστάσεων;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 6 Αυγούστου, 2009 @ 6:21 μμ
Καλησπέρα και πάλι 🙂
Ας γίνω πιο αναλυτικός.
Καθε ένας απο τους περιγεγραμμένους κύκλους εχει σαν χορδή ενα ευθύγραμμο τμήμα που ενώνει δύο απο τις πόλεις. Επειδή πρόκειται για περιγεγραμμένους κύκλους ισόπλευρων τριγώνων, το αντίστοιχο τόξο φαίνεται από τα σημεία του κύκλου είτε υπο οξεία γωνία 60° (στο εξωτερικό του τριγώνου των πόλεων), είτε υπό αμβλεία 180°-60°=120° που είναι και η περίπτωση που μας ενδιαφέρει (εσωτερικό του τριγώνου των πόλεων).
Δύο τετοιοι κύκλοι, τώρα, θα τεμνονται σε δύο σημεία: σε μία απο τις πόλεις, την Α για παράδειγμα και, επειδή το τρίγωνο των πόλεων δεν έχει γωνία μεγαλύτερη των 120, σε ένα ακόμη το οποίο είναι εσωτερικό του τριγώνου αυτού και βλέπει τις ΑΒ και ΑΓ υπο 120°.
Προφανώς αυτό θα βλέπει και τς ΒΓ υπο 360°-120°-120°=120°. Αρα ανήκει και στον τρίτο κύκλο.
Θελετε να διεκρινιστεί και γιατί θελουμε γωνία 120° ως απαίτηση για την ελαχιστοποίηση;
Μου αρέσει!Μου αρέσει!
Σχόλιο από yioryos — 21 Αυγούστου, 2009 @ 1:59 πμ
Ωραία. Ας συνοψίσουμε λίγο όσα έχουν ειπωθεί στην κατεύθυνση της λύσης του προβλήματος για να δούμε τι απομένει να δειχτεί….
Από το πείραμα με τις σφαίρες και το τραπέζι είδαμε ότι αν το σύστημα ισορροπήσει με τον κόμπο να μην πέφτει μέσα σε μια από τις κορυφές τότε το σημείο που βρίσκεται ο κόμπος είναι στο εσωτερικό του τριγώνου και βλέπει τις πλευρές υπό γωνία 120 μοιρών. Ως σημείο ισορροπίας θα είναι κρίσιμο σημείο της δυναμικής ενέργειας ή ισοδύναμα του αθροίσματος των αποστάσεων από τις κορυφές. Μένει να δείξουμε ότι είναι και ΟΛΙΚΟ ελάχιστο της δυναμικής ενέργειας, οπότε το άθροισμα των αποστάσεων από τις κορυφές θα είναι ελάχιστο. ‘Οπως εξηγεί ο talsfan σε αυτή την περίπτωση όλες οι γωνίες του τριγώνου είναι <120 μοίρες.
Επόμένως αν σε ένα τρίγωνο υπάρχει γωνία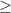
120 ο κόμπος θα πέσει σε μια από τις κορυφές και είναι εύκολο να δεί κανείς ότι αυτή ελαχιστοποιεί το άθροισμα των αποστάσεων και είναι η κορυφή της αμβλείας γωνίας.
Αν πάλι όλες οι γωνίες του τριγώνου είναι <120, σύμφωνα με το σχόλιο του yioryos υπάρχει σημείο στο εσωτερικό του τριγώνου που κατασκευάζεται με κανόνα και διαβήτη και βλέπει όλες τις πλευρές του τριγώνου υπό γωνία 120 μοιρών. Μπορεί κανείς να δείξει γεωμετρικά ότι στο σημείο αυτό το άθροισμα των αποστάσεων από τις κορυφές θα είναι ελάχιστο. Πιο εύκολα όμως, χρησιμοποιώντας πάλι την ιδέα από τη φυσική, οι δυνάμεις από τις σφαίρες ισορροπούν όταν ο κόμπος βρίσκεται στο σημείο αυτό, άρα το σημείο αυτό είναι κρίσιμο για τη δυναμική ενέργεια του συστήματος (ή ισοδύναμα το άθροισμα των αποστάσεών του από τις κορυφές του τριγώνου.)
Αυτό που απομένει λοιπόν για μια πλήρη απόδειξη είναι να δείξουμε ότι αν ένα σημείο στο εσωτερικό του τριγώνου είναι κρίσιμο για το άθροισμα των αποστάσεων του από τις κορυφές του τριγώνου, τότε είναι και το σημείο που ελαχιστοιεί αυτό το άθροισμα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 21 Αυγούστου, 2009 @ 3:29 μμ
Αν τα σημεια ειναι συνευθειακα, τοτε το ζητουμενο σημειο ειναι η πολη που εχει εκατέρωθέν της, πολεις. Αν τα σημεια σχηματιζουν τριγωνο τοτε το ζητουμενο σημειο ειναι το Fermat-Torricelli σημειο του τριγωνου αυτου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από rallis (@rallis22) — 19 Ιουλίου, 2012 @ 2:29 μμ
Πράγματι έτσι ονομάζεται και μπορεί κανείς να βρει μια καθαρά γεωμετρική απόδειξη. Προσπαθούμε όμως να τελειώσουμε το επιχείρημα με την ισορροπία των σφαιρών- και δεν είμαστε μακριά…
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 19 Ιουλίου, 2012 @ 2:42 μμ