Προβλήματα Μαθηματικών

28 Ιουνίου, 2015

Πάντα θετικό

Filed under: Λυμένα Προβλήματα — Mihalis Kolountzakis @ 11:59 μμ

positive

Δείξτε ότι το πολυώνυμο

p(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \cdots + \frac{x^{2n}}{(2n)!}

είναι πάντα θετικό (για κάθε x\in{\mathbb R}, n=1, 2, \ldots).

32 Σχόλια »

  1. αυτη δεν ειναι η σειρα taylor της e^x στο 0?? αρα ισουται με e^x που ειναι θετικη…

    Μου αρέσει!

    Σχόλιο από valeria fr — 29 Ιουνίου, 2015 @ 3:41 πμ

  2. Πολυώνυμο είναι.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 29 Ιουνίου, 2015 @ 7:10 πμ

  3. Αρκεί να δείξουμε ότι: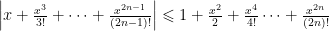 \left|x+\frac{x^{3}}{3!}+ \cdots + \frac{x^{2n-1}}{(2n-1)!}\right| \leqslant 1+\frac{x^{2}}{2}+\frac{x^{4}}{4!}\cdots+\frac{x^{2n}}{(2n)!} για κάθε 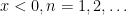x<0, n=1,2,\ldots για κάθε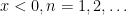 x<0, n=1,2,\ldots

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 29 Ιουνίου, 2015 @ 1:07 μμ

  4. To Σ(ν=0 έως άπειρο))(x^(2ν) /(2ν)!)=cosh (x). To κόζινους υπερμπόλικους του x είναι πάντα θετικό. Είναι (e^x +e^(-x))/2

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 29 Ιουνίου, 2015 @ 3:16 μμ

  5. 4. είναι >= 1

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 29 Ιουνίου, 2015 @ 3:17 μμ

  6. 4, 5: Δεν καταλαβαίνω. Η συνάρτηση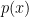 p(x) είναι πολυώνυμο, όχι άπειρη σειρά.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 29 Ιουνίου, 2015 @ 3:58 μμ

  7. @Κουζουρίδης: Αρκεί, αλλά πως;

    Εγώ προτείνω να δείξουμε ότι \forall x \leq 0 : e^x \leq p(x), με παραγώγους και επαγωγή.

    Μου αρέσει!

    Σχόλιο από sq81 — 29 Ιουνίου, 2015 @ 5:22 μμ

  8. Θα εκτιμούσα αν κάποιος μπορούσε να γράψει το πολυώνυμο p(x) για n=3. Eυχαριστώ!

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 30 Ιουνίου, 2015 @ 10:16 πμ

  9. Είναι το \sum_{k=0}^6 \frac{x^k}{k!}

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 30 Ιουνίου, 2015 @ 10:24 πμ

  10. Επειδή το πρόβλημα έχει τεθεί εδώ και κάμποσο καιρό και με «ξύνει» κάπως. Επειδή κάποιοι το συνέδεσαν με το ανάπτυγμα Taylor του εκθετικού, ο μονος τρόπος που η σειρά Taylor είναι χρήσιμη (σαν εργαλείο απόδειξης πάντα) είναι σαν πολυώνυμο Taylor + ορος σφάλματος. Αν θα μπορούσαμε να χρησιμοποιήσουμε κάτι τέτοιο, έχει καλώς …

    Μου αρέσει!

    Σχόλιο από Ioannis Markou — 8 Ιουλίου, 2015 @ 5:00 πμ

  11. Μια άλλη ιδέα λύσης. Αφού ο ισχυρισμός είναι ότι είναι πάντα θετικό να το παραγοντοποιήσουμε για κάθε n και να δείξουμε ότι το πλήθος των μιγαδικών λύσεων είναι τόσο όσο και ο βαθμός του πολυωνύμου.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 8 Ιουλίου, 2015 @ 6:26 μμ

  12. Υπόδειξη: Εξετάστε το πρόσημο της συνάρτησης όπου έχει τοπικό ελάχιστο.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 11 Ιουλίου, 2015 @ 11:11 πμ

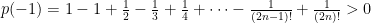  13. Ευχαριστούμε για την υπόδειξη. Αρκεί να δείξουμε ότι το πρόσημο της συνάρτησης-του πολυωνύμου μας, είναι θετικό σε όλα τα τοπικά ελάχιστα. Ως γνωστόν παραγωγίζουμε το πολυώνυμο μια φορά και ψάχνουμε τιμές για τις οποίες μηδενίζεται το p'(x). p'(x)=x^{2n-1}+x^{2n-2}+\dots+x+1=0 \Rightarrow x=-1. Αντικαθιστώντας τώρα στο πολυώνυμο p(-1)=1-1+\frac{1}{2}-\frac{1}{3}+\frac{1}{4}+\dots-\frac{1}{(2n-1)!}+\frac{1}{(2n)!}>0.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 11 Ιουλίου, 2015 @ 11:39 μμ

  14. Η τελευταία γραμμή είναι λάθος. $latex $p(-1)=1-1+\frac{1}{2}-\frac{1}{3}+\frac{1}{4}+\dots-\frac{1}{2n-1}+\frac{1}{2n}>0$.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 12:10 πμ

  15. p(-1)=1-1+\frac{1}{2}-\frac{1}{3}+\frac{1}{4}+\dots-\frac{1}{2n-1}+\frac{1}{2n}>0.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 12:11 πμ

  16. Συγνώμη. p(-1)=1-1+\frac{1}{2}-\frac{1}{3!}+\frac{1}{4!}+\dots-\frac{1}{(2n-1)!}+\frac{1}{(2n)!}>0.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 12:15 πμ

  17. p(-1)=\sum_{k=2}^{2n}\frac{(-1)^k}{k!}.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 12:29 πμ

  18. Κωνσταντίνε, δεν είναι το σημείο x=-1, το σημείο όπου υπάρχει ελάχιστο.Προσπάθησε να υπολογίσεις την παραγωγο σωστά και θα βρείς τη σχέση της με το πολυώνυμο p(x). Ειδάλλως μπορείς να δείξεις ότι e^x < p(x) (για x<0) χρησιμοποιώντας το ανάπτυγμα Taylor και εκτιμώντας τον ορο σφάλματος.

    Μου αρέσει!

    Σχόλιο από Ioannis Markou — 12 Ιουλίου, 2015 @ 7:16 πμ

  19. Ευχαριστώ. Ναι έκανα λάθος στον υπολογισμό της παραγώγου. Τώρα νομίζω είναι σωστό.
    p'(x)=0 \Rightarrow x^{2n-1}+(2n-1)x^{2n-2}+(2n-1)(2n-2)x^{2n-3}+\dots+(2n-1)!x=0. Κατάλληλα x που ικανοποιούν την παραπάνω εξίσωση είναι τα τοπικά ακρότατα. Τώρα να δούμε πώς θα τα βρούμε τώρα.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 10:18 πμ

  20. Ξέχασα τον σταθερό όρο. p'(x)=0 \Rightarrow x^{2n-1}+(2n-1)x^{2n-2}+(2n-1)(2n-2)x^{2n-3}+\dots+(2n-1)!x+(2n-1)!=0. Παραγώγισα το πολυώνυμο και πολλαπλασίασα όλους τους όρους με τον παρονομαστή του μεγιστοβάθμιου όρου, δηλαδή με το (2n-1)!.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 10:41 πμ

  21. 18. Ιωάννη, νομίζω δεν μπορεί να εκτιμηθεί το σφάλμα της συνάρτησης μας σε σχέση με το πολυώνυμο Taylor, και αυτό διότι το σφάλμα δεν είναι φραγμένο. Το x δεν είναι σταθερό και επίσης ούτε ο βαθμός του πολυωνύμου.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 11:00 πμ

  22. Επιμένω ότι πρέπει να υπολογίσεις την παραγωγο σωστά. Αν το κανεις σωστά θα δεις ότι η παραγωγος p'(x) περιέχει όλους τους ορους του p(x) εκτος από τον μεγιστοβάθμιο ορο x^{2n}/(2n)!

    Μου αρέσει!

    Σχόλιο από Ioannis Markou — 12 Ιουλίου, 2015 @ 9:14 μμ

  23. Σωστά. Είναι το ίδιο. p'(x)=\sum_{k=0}^{2n-1}\frac{x^k}{k!}=0. Πολλαπλασιάζοντας με (2n-1)!, κάθε όρο της εξίσωσης (αφού είναι ίση με μηδέν) προκύπτει η ισοδύναμη εξίσωση στο σχόλιο 20.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 9:34 μμ

  24. άρα μπορείς τώρα να χρησιμοποιήσεις την υπόδειξη που έδωσε ο Μιχάλης…»

    Υπόδειξη: Εξετάστε το πρόσημο της συνάρτησης όπου έχει τοπικό ελάχιστο»

    Μου αρέσει!

    Σχόλιο από Ioannis Markou — 12 Ιουλίου, 2015 @ 10:21 μμ

  25. Πρέπει να βρούμε κατάλληλα x όμως που να μηδενίζουν το p'(x). To μόνο που θυμάμαι είναι ένα θεώρημα που λέει ότι οποιοδήποτε πολυώνυμο περιττού βαθμού έχει πραγματική ρίζα. Φαντάζομαι θα υπάρχει κάποια σχέση που να συνδέει τις ρίζες με το βαθμό. Δεν βλέπω κάποια όμως.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 12 Ιουλίου, 2015 @ 10:54 μμ

  26. Δε χρειάζεται να υπολογίσεις (per σε) το σημείο όπου υπάρχει το ελάχιστο. Η ιδέα είναι να βρείς τι σημαίνει για το πρόσημο της p(x) στο σημείο ελαχιστου. Σκέψου αν μια συνάρτηση παίρνει και αρνητικές τιμές, τότε στο ελάχιστο της (αν υπάρχει αυτό πάντα!) θα πρέπει να είναι αρνητική. Τέλος, όταν το κανεις αυτό, καλο είναι να υποδείξεις γιατί το πολυώνυμο έχει και ελάχιστο (δες για παράδειγμα τι συμβαίνει όταν x τείνει +- άπειρο).

    Μου αρέσει!

    Σχόλιο από Ioannis Markou — 12 Ιουλίου, 2015 @ 11:40 μμ

  27. Θα κάνω μια προσπάθεια να συνοψίσω τις εξαιρετικές ιδέες των προηγηθέντων φίλων σχολιαστών:
    Το p(x) είναι πολυώνυμο άρτιου βαθμού με θετικό το συντελεστή του μεγιστοβάθμιου όρου, επομένως p(x) -> +∞ είτε χ->+∞ είτε χ->-∞, και σε κάποια ενδιάμεση τιμή χ, η τιμή του p(x) ελαχιστοποιείται.
    Η παραγώγιση του p(x) δίνει:
    p'(x) = 1+x+x^2/2+x^3/3!+…+x^(2n-1)/2n-1)! = p(x) – x^(2n)/(2n)! => p(x) = p'(x) + x^(2n)/(2n)! (1)
    Στην τιμή χ που ελαχιστοποιεί την τιμή του p(x), θα είναι p'(x)=0, ενώ x^(2n)/(2n)! > 0 για κάθε χ ≠ 0. Επομένως από την (1), θα έχουμε:
    min p(x) = 0 + x^(2n)/(2n)! > 0, αν χ ≠ 0.
    Αν πάλι χ=0, τότε p(x) = 1 > 0.
    Σε κάθε περίπτωση, p(x) > 0 ό.έ.δ.

    Μου αρέσει!

    Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 14 Ιουλίου, 2015 @ 12:00 μμ

  28. 27: Πολύ σωστά. Αυτή είναι η απόδειξη.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 14 Ιουλίου, 2015 @ 12:03 μμ

  29. Γνωρίζετε βιβλιογραφία για πολυώνυμα ακόμα και κατί σε προβλήματα+λύσεις;

    Μου αρέσει!

    Σχόλιο από nickaleha — 6 Απριλίου, 2016 @ 8:21 πμ

  30. 29: Μπορείς να γίνεις πιο συγκεκριμένος στο τι σε ενδιαφέρει;

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 6 Απριλίου, 2016 @ 8:37 πμ

  31. Λόγω του msc μου, θα με ενδιέφερε οποιοδήποτε βιβλίο με προβλήματα και λύσεις όπως το παραπάνω (ακόμα και αν ανήκουν στην κατηγορία elementary math) ή με προβλήματα στα οποία οι συντελεστές ανήκουν σε κάποιο σώμα ή δακτύλιο. Με ενδιαφέρει κυρίως η μαθηματική σκοπιά και όχι η αλγοριθμική, σε ελληνική ή αγγλική βιβλιογραφία.

    Μου αρέσει!

    Σχόλιο από nickaleha — 7 Απριλίου, 2016 @ 8:45 πμ

  32. 31: Ο supervisor μου (για το final year project του Bsc μου πάνω στη συνδυαστική) στην Αγγλία, Krasikov IIia, μου είχε πει ότι η έρευνα του έχει να κάνει με πολυώνυμα. Το ανάφερα διότι μπορεί να ξέρει βιβλιογραφία. Αν θες στείλε του ένα μήνυμα. Είναι στο Brunel.

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 27 Απριλίου, 2016 @ 11:21 μμ


RSS feed for comments on this post. TrackBack URI

Σχολιάστε

Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.