Προβλήματα Μαθηματικών

5 Μαΐου, 2011

Θα προλάβει όμως;

Filed under: Λυμένα Προβλήματα — Michalis Loulakis @ 7:59 μμ

Στο προηγούμενο πρόβλημα είδαμε ότι ο φοιτητής μπορεί να ποντάρει 1 ευρώ κάθε φορά και αυτό του εξασφαλίζει τη μέγιστη πιθανότητα να συμπληρώσει τα 1000 ευρώ που χρειάζεται για να πάει διακοπές. Δείξτε ότι  δεδομένου ότι φτάνει τα 1000 ευρώ, ο αναμενόμενος αριθμός στοιχημάτων μέχρι να συμπληρώσει αυτό το ποσό είναι 333.333.

4 Σχόλια »

  1. Έστω Α το ενδεχόμενο να φτάσει τα 1000 ευρώ.
    Στο προηγούμενο πρόβλημα είδαμε ότι
    \mathbb{P}[A|F_0 = 1] = 1/1000 .
    Δεδεμένου ότι κάθε φορά ποντάρει 1 ευρώ και λόγω
    ανεξαρτησίας, έχουμε πως αν σε κάποια χρονική στιγμή, t,
    η περιουσία του είναι κ ευρώ, 1<κ0.

    Ακριβώς το ίδιο επιχείρημα με το προηγούμενο πρόβλημα δείχνει ότι
    p_k := \mathbb{P}[A|F_0 = k] = k/1000 .
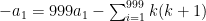
    Συνεπώς, η πιθανότητα να κερδίσει στη πρώτη ρίψη (δεδομένου ότι φτάνει τα 1000 ευρώ) είναι
    \mathbb{P}[F_1 = 2|A] = \frac{1}{2} \frac{p_2}{p_1} = 1 και γενικότερα,
    αν σε κάποια χρονική στιγμή t έχει περιουσία κ, η πιθανότητα να αυξήσει την
    περιουσία του κατά 1 είναι \frac{k+1}{2k} .
    Έστω T_k ο χρόνος που χρειάζεται για να φτάσει τα 1000 ευρώ
    έχοντας περιουσία κ, έστω a_k = \mathbb{E}[T_k|A].
    Τότε
    a_k = (1+a_{k+1}) \frac{k+1}{2k} + (1+a_{k-1})\frac{k-1}{2k} ή
    2ka_k = (k+1)a_{k+1} + (k-1) a_{k-1} + 2k ή
    (k+1)a_{k+1} - k a_k = k a_k - (k-1) a_{k-1} - 2k και άρα
    (k+1)a_{k+1} - k a_k = a_1 - k(k+1) .
    Αθροίζουμε τις ΄ανω σχέσεις για κ=1,2,..999 και έχουμε
    - a_1 = 999 a_1 - \sum_{i=1}^{999}k(k+1)
    και άρα a_1 = \frac{999\cdot 2002}{6} = 333.333 .

    Μου αρέσει!

    Σχόλιο από henk&christos — 13 Μαΐου, 2011 @ 4:18 μμ

  2. ‘Έφαγε’ λίγο από το σχόλιο της 1ης παραγράφου..

    ..αν σε κάποια χρονική στιγμή, t, η περιουσία του είναι
    κ ευρώ, 1<κ<1000, τότε
    \mathbb{P}[A| F_t = k] = \mathbb{P}[A|F_0 = k]

    Μου αρέσει!

    Σχόλιο από henk&christos — 13 Μαΐου, 2011 @ 4:24 μμ

  3. Ξέχασα επίσης να γράψω πως για την επίλυση της αναδρομικής σχέσης
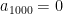    χρησιμοποιούμε το γεγονός ότι
    a_{1000} = 0.

    Μου αρέσει!

    Σχόλιο από henk&christos — 13 Μαΐου, 2011 @ 5:27 μμ

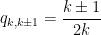  4. Πολύ ωραία. Η βασική ιδέα εδώ είναι να παρατηρήσει κανείς ότι η μαρκοβιανή αλυσίδα μας δεδομένου του ενδεχομένου A είναι μια νέα μαρκοβιανή αλυσίδα με πιθανότητες μετάβασης \displaystyle q_{k,k\pm1}=\frac{k\pm1}{2k}. Μ’ άλλα λόγια, η δέσμευση ότι ο τυχαίος περίπατος φτάνει στο δεξί άκρο είναι ισοδύναμη με το να αλλάξουμε τις πιθανότητες μετάβασης σε κάθε θέση, δίνοντας μια τάση στον περίπατο να πηγαίνει δεξιά, όπως δείχνει η παραπάνω σχέση. Με αυτήν την παρατήρηση, το πρόβλημα ανάγεται στον υπολογισμό του αναμενόμενου χρόνου άφιξης στο δεξί ακρο για μια διαδικασία γεννήσεως/θανάτου που λύνεται ακριβώς όπως μας περιέγραψες καταστρώνοντας μια αναδρομική σχέση.

    Για να δούμε λίγο πιο αναλυτικά αυτό που γράφεις «και γενικότερα, αν σε κάποια χρονική στιγμή t έχει περιουσία κ, η πιθανότητα να αυξήσει την περιουσία του κατά 1 είναι \frac{k\pm1}{2k} προσέξτε ότι αν q_{m,m\pm 1}=\mathbb{P}[X_{n+1}=m\pm 1 | X_n=m,\ A], τότε

    \displaystyle q_{m,m\pm 1}= \frac{\mathbb{P}[A | X_{n+1}=m\pm 1,\ X_n=m]\mathbb{P}[X_{n+1}=m\pm 1\ |\ X_n =m]\mathbb{P}[X_n=m]}{\mathbb{P}[A\ |\ X_n=m]\mathbb{P}[X_n=m]}, ή
    \displaystyle q_{m,m\pm 1}=\frac{\mathbb{P}[A | X_{n+1}=m\pm 1]\times 1/2}{\mathbb{P}[A\ |\ X_n=m]}

    όπου χρησιμοποιήσαμε τη μαρκοβιανή ιδιότητα για τους πρώτους δύο όρους του αριθμητή. Τέλος χρησιμοποιώντας ότι \mathbb{P}[A|X_n=m]=m/1000 έχουμε το ζητούμενο.

    Μου αρέσει!

    Σχόλιο από Michalis Loulakis — 15 Μαΐου, 2011 @ 3:51 μμ


RSS feed for comments on this post. TrackBack URI

Σχολιάστε

Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.