Δείξτε ότι για κάθε η απόσταση του
από τον πλησιέστερό του ακέραιο είναι μικρότερη από
.
17 Νοεμβρίου, 2008
Σχεδόν ακέραιος
5 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Δείξτε ότι για κάθε η απόσταση του
από τον πλησιέστερό του ακέραιο είναι μικρότερη από
.
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Πως γίνεται να γράψει κάποιος σε latex; Κάνω μια δοκιμή…
[tex]\frac12 < \left\lfloor \mathrm{mod} \left( \left\lfloor \frac{y}{17}\right\rfloor 2^{-17\lfloor x\rfloor -\mathrm{mod}(\lfloor y\rfloor , 17)},2\right)\right\rfloor[/tex]
Μου αρέσει!Μου αρέσει!
Σχόλιο από ctzamos — 21 Νοεμβρίου, 2008 @ 1:24 μμ
Μου αρέσει!Μου αρέσει!
Σχόλιο από ctzamos — 21 Νοεμβρίου, 2008 @ 1:25 μμ
Για να γράψετε σε latex γράψτε ως εξής
$ latex {1+1=2}$
όπου το κενό ανάμεσα στο 1ο δολλάριο και τη λέξη latex δεν υπάρχει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Νοεμβρίου, 2008 @ 1:34 μμ
ΟΚ ευχαριστώ και συγνώμη για τα άκυρα post…
Ελπίζω να φανεί
Παίρνοντας τη διαφορά με το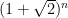 έχουμε
έχουμε
Όμως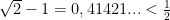
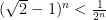
Άρα
Μου αρέσει!Μου αρέσει!
Σχόλιο από ctzamos — 21 Νοεμβρίου, 2008 @ 1:45 μμ
Για κάποιο λόγο τα σχόλιά σου θεωρήθηκαν spam αυτόματα από το σύστημα και δεν το πήρα χαμπάρι παρά μόνο σήμερα. Η λύση σου πάντως είναι βέβαια σωστή.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Νοεμβρίου, 2008 @ 11:24 μμ