Το ορθογώνιο τρίγωνο με πλευρές 6,8 και 10 έχει περιμέτρο 24 και εμβαδόν 24. Υπάρχουν λίγα ακόμα τρίγωνα με πλευρές που έχουν ακέραιο μήκος και περίμετρο ίση με το εμβαδόν τους. Βρείτε τα.
Προβλήματα Μαθηματικών
ΠΡΟΒΛΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
-
Πρόσφατα σχόλια
Mihalis Kolountzakis στο Πεπερασμένοι μετρικοί χώρ… alexandrosg στο Πεπερασμένοι μετρικοί χώρ… Mihalis Kolountzakis στο Πεπερασμένοι μετρικοί χώρ… alexandrosg στο Πεπερασμένοι μετρικοί χώρ… Themis Mitsis στο Χωριστά συνεχής christosmix στο Χωριστά συνεχής Themis Mitsis στο Χωριστά συνεχής christosmix στο Χωριστά συνεχής Themis Mitsis στο Χωριστά συνεχής christosmix στο Χωριστά συνεχής Michalis Loulakis στο Αριθμοί Liouville II Mihalis Kolountzakis στο Μη αρνητικά πολυώνυμα yannisanag στο Αριθμοί Liouville II yannisanag στο Αριθμοί Liouville II nikos3223 στο Μη αρνητικά πολυώνυμα
Ορθογώνιο τρίγωνο με πλευρές 3,4,5.
Comment από charav — Ιουνίου 21, 2009 @ 4:29 μμ
Συγχωρέστε με. Λάθος απο κεκτημένη ταχύτητα.
Comment από charav — Ιουνίου 21, 2009 @ 4:30 μμ
Εστω χ,ψ,ζ οι πλευρες του ζητουμενου τριγωνου, θελουμε να ισχυουν τα εξης : χ^2 + ψ^2 = ζ^2 και 1/2(χψ)=χ + ψ + ζ . Λυνοντας το συστημα τών διοφαντικών εξισώσεων καταληγουμε σε μια σχεση της μορφης χψ + 8 = 4χ + 4ψ λυνοντας ως προς χ περνουμε
χ = (8-4ψ)/(4-ψ) ή χ = 4 – 8/4-ψ και επειδη θελουμε ο χ να ειναι ακέραιος (και > 0) 8α πρεπει το κλασμα να ειναι ακέραιο δηλαδή το 4-ψ να είναι διαιρέτης του 8.
Ετσι περνουμε 4-ψ = +- 8 ή +-4 ή +- 2 ή +-1 ==> ψ = -4 ή 0 ή 2 ή 3 ή 5 ή 6 ή 8 ή 12
Προφανώς οι 2 πρώτες απορίπτονται γιατι το ψ εκφράζει μηκος οπότε αντικα8ιστούμε στην σχέση χ = 4 8/4-ψ τα ψ που βρήκαμε και περνουμε :
χ = 0 ή -4 ή 12 ή 8 ή 6 ή 5 πάλι οι 2 πρώτες αποριπτονται και ετσι μας μενουν οι 2 πυθαγόριες τριάδες (5,12,13) και (6,8,10)
απέφυγα να γραψω τις πολλες πράξεις γιατι δεν εχω ιδέα πως να γραφω με μαθηματικα σύμβολα
Comment από mcdallas — Ιουνίου 24, 2009 @ 3:54 μμ
Αυτά είναι τα ορθογώνια τρίγωνα που έχουν την ιδιότητα. Υπάρχουν και μερικά που δεν είναι ορθογώνια…
Comment από Michalis Loulakis — Ιουνίου 24, 2009 @ 6:33 μμ
Λαθος μου δε το διαβασα σωστα νομιζα ψαχναμε μονο ορθογωνια γι αυτο παραξενευτηκα που βρηκα μονο 1 οταν ειπες “λιγα”
Comment από mcdallas — Ιουνίου 24, 2009 @ 7:00 μμ
Από τον τύπο του Ήρωνα για το εμβαδό του τριγώνου προκύπτει ότι αρκεί να βρούμε φυσικούς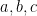
τέτοιους ώστε να ισχύει 
.
και η παραπάνω είναι ισοδύναμη με την 
(1).
.
(2).
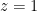
από την οποία παίρνουμε τις λύσεις 
ή 
.
ή 
.
, η (2) γίνεται 
από την οποία παίρνουμε τις λύσεις 
ή 
.
, η (2) έχει λύση την 
η οποία δεν είναι αποδεκτή γιατί 
.
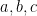είναι τα εξής:
.
Από την παραπάνω παρατηρούμε ότι τουλάχιστον ένας παράγοντας του αριστερού μέλους είναι άρτιος, άρα όλοι είναι άρτιοι.
Θέτουμε λοιπόν
Χωρίς βλάβη της γενικοτητας υποθέτουμε ότι
Η (1) είναι ισοδύναμη με την
Διακρίνουμε τώρα δύο περιπτώσεις.
1η Περίπτωση:
Η (2) γίνεται
2η Περίπτωση:
Ισχύει
Αν
Αν
Άρα τελικά βρήκαμε 5 λύσεις για τις οποίες τα αντίστοιχα
Comment από stedes — Ιουλίου 18, 2009 @ 5:41 μμ
Σωστά. Πολύ ωραία λύση.
Comment από Michalis Loulakis — Ιουλίου 18, 2009 @ 6:37 μμ