Ας είναι μια συνάρτηση με πεδίο ορισμού τους ακεραίους. Ένας φυσικός αριθμός
λέγεται περίοδος της
αν
. Αν υπάρχει τέτοιο
τότε η
λέγεται περιοδική. Έυκολα βλέπει κανείς ότι η ελάχιστη περίοδος μιας περιοδικής συνάρτησης διαιρεί κάθε άλλη περίοδο και ότι κάθε πολλαπλάσιο περιόδου είναι κι αυτό περίοδος.
Αν είναι δύο φυσικοί αριθμοί πρώτοι μεταξύ τους και
δυο συναρτήσεις επί των ακεραίων με ελάχιστη περίοδο
και
αντίστοιχα δείξτε ότι η συνάρτηση
είναι επίσης περιοδική και μάλιστα με ελάχιστη περίοδο το
. (Η έμφαση είναι στο «ελάχιστη».)
Τι λέτε για την ελάχιστη περίοδο της αν οι
δεν είναι μεταξύ τους πρώτοι;
Καταρχάς, εύχομαι καλή δύναμη σε όλους , διαχειριστές, εισηγητές και φίλους του ιστότοπου για τη νέα περίοδο 🙂
Θα σπάσω το σχόλιό μου στα δύο, γιατί δε μου το δέχεται ολόκληρο.
Έχω την εντύπωση ότι το θέμα είναι αρκετά συνθετότερο από όσο δείχνει, αλλά δεν μπορώ να αποκλείσω κάποια ‘μαγική’ προσέγγιση που ενοποιεί τις διάφορες υποπεριπτώσεις.
Ο αβ είναι πολλαπλάσιος τόσο του α, όσο και του β, άρα είναι περίοδος τόσο της f, όσο και της g, δηλαδή f(x+αβ)=f(x) και g(x+αβ)=g(x) => f(x+αβ)+g(x+αβ) = f(x)+g(x), για κάθε xєΖ. Επομένως ο αβ είναι περίοδος και της f+g.
Για την απόδειξη ότι ο αβ είναι η ελάχιστη περίοδος της f+g, διακρίνουμε περιπτώσεις:
1. Αν α=β=1, τότε αβ=1 και ο αβ είναι η ελάχιστη περίοδος της f+g, αφού ισούται με τον ελάχιστο φυσικό αριθμό.
2. Αν α>1 και β=1, τότε αβ=α.
Αν ο α δεν ήταν η ελάχιστη περίοδος της f+g, τότε η ελάχιστη περίοδος θα ήταν κάποιος θετικός ακέραιος 1≤γ<α, με τον γ να διαιρεί τον α. Θα είχαμε:
f(x+γ)+g(x+γ)=f(x)+g(x), για κάθε xєΖ (1).
Ο γ ως πολλαπλάσιος του β=1 θα ήταν και περίοδος της g, οπότε:
g(x+γ)=g(x), για κάθε xєΖ (2).
Αφαιρώντας κ.μ. από την (1) τη (2) παίρνουμε:
f(x+γ)=f(x), για κάθε xєΖ , δηλαδή ο γ θα ήταν και περίοδος της f. Αντίφαση, αφού γ1.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 1:18 μμ
(επανάληψη περίπτωσης 2)
2. Αν α>1 και β=1, τότε αβ=α.
Αν ο α δεν ήταν η ελάχιστη περίοδος της f+g, τότε η ελάχιστη περίοδος θα ήταν κάποιος θετικός ακέραιος 1≤γ<α, με τον γ να διαιρεί τον α. Θα είχαμε:
f(x+γ)+g(x+γ)=f(x)+g(x), για κάθε xєΖ (1).
Ο γ ως πολλαπλάσιος του β=1 θα ήταν και περίοδος της g, οπότε:
g(x+γ)=g(x), για κάθε xєΖ (2).
Αφαιρώντας κ.μ. από την (1) τη (2) παίρνουμε:
f(x+γ)=f(x), για κάθε xєΖ , δηλαδή ο γ θα ήταν και περίοδος της f. Αντίφαση, αφού γ1.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 1:24 μμ
(Ξανά η περίπτωση 2)
2. Αν α>1 και β=1, τότε αβ=α.
Αν ο α δεν ήταν η ελάχιστη περίοδος της f+g, τότε η ελάχιστη περίοδος θα ήταν κάποιος θετικός ακέραιος 1≤γ1.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 1:26 μμ
2. Αν α μεγαλύτερος του 1 και β=1, τότε αβ=α.
Αν ο α δεν ήταν η ελάχιστη περίοδος της f+g, τότε η ελάχιστη περίοδος θα ήταν κάποιος θετικός ακέραιος 1≤γ και γ μικρότερος του α, με τον γ να διαιρεί τον α. Θα είχαμε:
f(x+γ)+g(x+γ)=f(x)+g(x), για κάθε xєΖ (1).
Ο γ ως πολλαπλάσιος του β=1 θα ήταν και περίοδος της g, οπότε:
g(x+γ)=g(x), για κάθε xєΖ (2).
Αφαιρώντας κ.μ. από την (1) τη (2) παίρνουμε:
f(x+γ)=f(x), για κάθε xєΖ , δηλαδή ο γ θα ήταν και περίοδος της f. Αντίφαση, αφού ο γ μικρότερος του α και o α είναι η ελάχιστη περίοδος της f.
Τα ανάλογα ισχύουν και αν α=1 και β μεγαλύτερος του 1.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 1:44 μμ
3. Αν α και β μεγαλύτεροι του 1 με α≠β (αφού οι α και β είναι πρώτοι μεταξύ τους), τότε αν ο αβ δεν ήταν η ελάχιστη περίοδος της f+g, αυτή θα έπρεπε να είναι κάποιος θετικός ακέραιος γ, με γ≥1 και γ μικρότερος του αβ με τον γ να διαιρεί τον αβ.
Αν γ=1, τότε ο α ως πολλαπλάσιος του 1, θα ήταν κι αυτός περίοδος της f+g, οπότε θα ίσχυε:
f(x+α)+g(x+α)=f(x)+g(x) άρα g(x+α)=g(x), για κάθε xєΖ, οπότε ο α θα ήταν περίοδος και της g.
Ομοίως, ο β ως πολλαπλάσιος του 1, θα ήταν κι αυτός περίοδος της f+g, οπότε θα ίσχυε:
f(x+β)+g(x+β)=f(x)+g(x) άρα f(x+β)=f(x), για κάθε xєΖ, οπότε ο β θα ήταν περίοδος και της f.
Αντίφαση, αφού α≠β και ο μικρότερος από αυτούς δεν μπορεί να είναι περίοδος της συνάρτησης που έχει ελάχιστη περίοδο τον μεγαλύτερο.
Αν γ μεγαλύτερος του 1, τότε ο γ θα έπρεπε να είναι διαιρέτης αποκλειστικά του ενός από τους α και β.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 1:47 μμ
Δυστυχώς, δε μου δέχεται το τελευταίο μέρος του σχολίου, οπότε θα επιχειρήσω να το στείλω αργότερα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 2:48 μμ
Έστω ότι ο γ είναι διαιρέτης του a, οπότε ο a ως πολλαπλάσιος του γ θα είναι κι αυτός περίοδος της f+g και θα είναι f(x+a)+g(x+a) = f(x)+g(x), για κάθε χ € Ζ. Αφού όμως ο a είναι περίοδος της f, θα είναι και f(x+a) = f(x), για κάθε χ € Ζ. Επομένως θα είναι και g(x+a) = g(x), για κάθε χ € Ζ, οπότε ο a είναι και περίοδος της g. Δεδομένου όμως ότι η ελάχιστη περίοδος της g είναι o b, τότε ο a θα είναι αναγκαστικά πολλαπλάσιος του b. Άτοπο, αφού οι a και b είναι σχετικά πρώτοι.
Σε κάθε περίπτωση, ο ab είναι η ελάχιστη περίοδος της f+g.
Στην περίπτωση που οι a,b δεν είναι σχετικά πρώτοι, νομίζω ότι με ανάλογο τρόπο μπορεί να αποδειχθεί ότι η ελάχιστη περίοδος της f+g είναι το ΕΚΠ(a,b).
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 11 Σεπτεμβρίου, 2015 @ 4:36 μμ
1-7: Σωστά, αλλά νομίζω το έμπλεξες χωρίς λόγο. Ας το μαζέψω λιγάκι παρακάτω:
Ας υποθέσουμε ότι είναι μια περίοδος της
είναι μια περίοδος της  . Αφού είναι φανερό ότι το
. Αφού είναι φανερό ότι το  είναι μια περίοδος (αφού είναι περίοδος και για την
είναι μια περίοδος (αφού είναι περίοδος και για την  και για τη
και για τη  ) αρκεί να δείξουμε ότι
) αρκεί να δείξουμε ότι  . Αυτό μας δείχνει ότι το
. Αυτό μας δείχνει ότι το  είναι η ελάχιστη περίοδος.
είναι η ελάχιστη περίοδος.
Αν το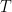 είναι περίοδος τότε και κάθε πολλαπλάσιό του είναι οπότε ισχύει
είναι περίοδος τότε και κάθε πολλαπλάσιό του είναι οπότε ισχύει
Για έχουμε ότι οι όροι με
έχουμε ότι οι όροι με  αριστερά και δεξιά είναι ίσοι (αφού κάθε πολλαπλάσιο του
αριστερά και δεξιά είναι ίσοι (αφού κάθε πολλαπλάσιο του  είναι περίοδος της
είναι περίοδος της  ), άρα, διαγράφοντας τους όρους αυτούς, έχουμε
), άρα, διαγράφοντας τους όρους αυτούς, έχουμε
Αυτό σημαίνει ότι το είναι περίοδος της
είναι περίοδος της  , άρα διαιρείται από την ελάχιστη περίοδο της
, άρα διαιρείται από την ελάχιστη περίοδο της  , δηλ. το
, δηλ. το  :
:
από το οποίο βγαίνει αφού τα
αφού τα  δεν έχουν κοινούς παράγοντες. Ομοίως
δεν έχουν κοινούς παράγοντες. Ομοίως  και άρα, αφού τα
και άρα, αφού τα  δεν έχουν κοινούς παράγοντες, έχουμε
δεν έχουν κοινούς παράγοντες, έχουμε  , που είναι αυτό που θέλαμε να δείξουμε.
, που είναι αυτό που θέλαμε να δείξουμε.
Θέλω όμως να επαναλάβω το ερώτημά μου για το τί γίνεται στην περίπτωση που τα δεν είναι μεταξύ τους πρώτοι.
δεν είναι μεταξύ τους πρώτοι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 12 Σεπτεμβρίου, 2015 @ 12:40 μμ
Όταν τα έχουν κοινούς παράγοντες η ελάχιστη περίοδος της
έχουν κοινούς παράγοντες η ελάχιστη περίοδος της  δεν είναι κατ’ ανάγκη το ελάχιστο κοινό πολλαπλάσιο των
δεν είναι κατ’ ανάγκη το ελάχιστο κοινό πολλαπλάσιο των  . Υπάρχουν δηλ. περιπτώσεις συναρτήσεων που η περίοδος του αθροίσματός τους είναι μικρότερη από το ελάχιστο κοινό πολλαπλάσιο των
. Υπάρχουν δηλ. περιπτώσεις συναρτήσεων που η περίοδος του αθροίσματός τους είναι μικρότερη από το ελάχιστο κοινό πολλαπλάσιο των  .
.
Σαφώς και υπάρχουν περιπτώσεις όπου η ελάχιστη περίοδος της
όπου η ελάχιστη περίοδος της  είναι το ΕΚΠ των
είναι το ΕΚΠ των  . Αλλά η πρόταση
. Αλλά η πρόταση
δεν είναι σωστή (η ελάχιστη περίοδος μπορεί είναι μικρότερη, διαιρέτης του ΕΚΠ).
Ποια είναι η μεγαλύτερη συνάρτηση που κάνει την παρακάτω πρόταση αληθή;
που κάνει την παρακάτω πρόταση αληθή;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 14 Σεπτεμβρίου, 2015 @ 10:28 μμ
Η ανάλυση(!!) στο σχόλιο 8 μπορεί να χρησιμοποιηθεί, μέχρις ενός σημείου, και στην περίπτωση που οι α και β έχουν κοινούς παράγοντες. Σε αυτή την περίπτωση, φτάνουμε μέχρι το σημείο που δείχνουμε ότι για οποιαδήποτε περίοδο Τ της f+g, θα πρέπει ο α να διαιρεί τον βΤ και ο β να διαιρεί τον αΤ.
Τώρα όμως με τους α,β όχι πλέον σχετικά πρώτους έχουμε:
α=ΜΚΔ(α,β)*κ και β=ΜΚΔ(α,β)*λ, με κ,λ σχετικά πρώτους, οπότε οι πιο πάνω συνθήκες συνεπάγονται ότι θα πρέπει ο κ να διαιρεί τον λΤ και ο λ τον κΤ, και αφού κ,λ σχετικά πρώτοι, πρέπει ο κλ να διαιρεί τον Τ.
Ο κλ μπορεί να γραφεί ως συνάρτηση των α,β, αν πάρουμε υπόψη ότι για οποιουσδήποτε φυσικούς αριθμούς α,β ισχύει ΜΚΔ(α,β)*ΕΚΠ(α,β) = αβ, οπότε κλ = αβ / [ΜΚΔ(α,β)]^2 => κλ = ΕΚΠ(α,β)/ΜΚΔ(α,β)
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 15 Σεπτεμβρίου, 2015 @ 1:36 μμ
10: Πολύ σωστά.
Όμως μέχρι στιγμής έχει απλά αποδειχτεί ότι η ποσότητα ΕΚΠ(α,β)/ΜΚΔ(α,β) διαιρεί κάθε περίοδο. Δεν έχει αποδειχτεί ακόμη το ότι αυτό είναι το καλύτερο που μπορούμε να πούμε γενικά (χωρίς δηλ. άλλες προϋποθέσεις για τις συναρτήσεις). Χρειάζεται ακόμη κάποιο παράδειγμα που να μας λέει ότι αυτή η ποσότητα όντως μπορεί να είναι η ελάχιστη περίοδος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 15 Σεπτεμβρίου, 2015 @ 1:42 μμ
Με πιο απλά λόγια: μπορείτε να φτιάξετε μια συνάρτηση με ελάχιστη περίοδο 10 και άλλη μια με ελάχιστη περίοδο 15 των οποίων το άθροισμα έχει ελάχιστη περίοδο 6;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 16 Σεπτεμβρίου, 2015 @ 1:01 πμ
Νομίζω ότι, από τις τριγωνομετρικές τουλάχιστον συναρτήσεις που ορίζονται για κάθε χ€Ζ, με το χ να εκφράζει μοίρες γωνίας, οι ημ(36χ) και συν(36χ) έχουν ελάχιστη περίοδο 10, ενώ οι ημ(24χ) και συν(24χ) έχουν ελάχιστη περίοδο 15. Είναι όμως ένα θέμα πώς μπορούμε να συνθέσουμε από αυτές κατάλληλες συναρτήσεις f και g, ώστε η f+g να έχει ελάχιστη περίοδο 6 :-).
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 16 Σεπτεμβρίου, 2015 @ 4:37 μμ
Είναι καλύτερο να σκέφτεται κανείς, ειδικά όταν ψάχνει για παραδείγματα, με συναρτήσεις που δε δίνονται από «τύπους». Φτιάξτε τη συνάρτησή σας ώστε να έχει τις ιδιότητες που εσείς θέλετε, κι ας μη δίνεται από κάποιο τύπο. Εξίσου καλή θα είναι, και πολύ ευκολότερο να την κατασκευάσει κανείς.
Η αγαπημένη μου ιστορία, σχετικά με το ότι μια συνάρτηση δε χρειάζεται να δίδεται από τύπο για να έχει καλές ιδιότητες, είναι η παρακάτω:
Έχω ένα επισκέπτη από την Αμερική το καλοκαίρι και τον έχω πάει από το σπίτι των γονιών μου στο χωριό, όπου η μητέρα μου μας έχει βάλει να φάμε στο μπαλκόνι, κι εκεί που τρώμε μαζεύονται καμιά δεκαριά γάτες από τη γειτονιά γύρω μας και κλαψουρίζουν για να τους δώσουμε λιχουδιές. Εντυπωσιασμένος ο καλεσμένος μου με τις τόσες γάτες (σημειωτέον ότι στην Αμερική, στα πλούσια κομμάτια της κυρίως, δεν υπάρχουν αδέσποτα ζώα) ρωτάει τη φοβερή ερώτηση:
«Πώς τις λένε;»
Τώρα, όσοι έχουν βρεθεί σε παρόμοιο περιβάλλον στην Ελλάδα ξέρει ότι οι γάτες είναι τόσες που κανείς δε σκέφτεται να τις ονοματίσει. Αλλά για ένα Αμερικάνο αυτό είναι πρωτόγνωρο:
-How can you not have any names for them???
Η απάντηση του πατέρα μου ήταν: εσύ χρειάζεσαι να έχεις όνομα για τις γάτες, αλλά αυτές δεν το χρειάζονται.
Έτσι και για τις συναρτήσεις στα Μαθηματικά: μια συνάρτηση μπορεί να έχει πολύ καλές ιδιότητες (ή, εν πάσει περιπτώσει, αυτές τις ιδιότητες που εμείς θέλουμε) και να μη δίνεται από ένα ωραίο και βραχύ τύπο, αλλά να μπορεί να περιγραφεί πολύ εύκολα «περιφραστικά».
Απελευθερωθείτε λοιπόν από την ονοματολογία: τα ονόματα είναι λίγα, τα αντικείμενα είναι πολλά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Σεπτεμβρίου, 2015 @ 12:01 πμ
Το να βαφτίζεις τα γατιά έχει μιά δυσκολία….
Δεν είναι επιπόλαιη κι ανάλαφρη ασχολία
Καθόλου δεν τρελάθηκα, και δεν το λέω αστεία:
Κάθε μιά Γάτα, ΟΝΟΜΑΤΑ ΠΡΕΠΕΙ ΝΑ ΕΧΕΙ ΤΡΙΑ!
Ένα, να τη φωνάζουμε στην οικογένειά της
Ας πούμε Βίκτωρ, Αύγουστος, Τζωρτζίνα, Ιπποκράτης
Ας πούμε Μέρλιν, Τζόναθαν, Αλόνζο, Μανταλένα
Καθημερινά ονόματα, καλά συνηθισμένα.
Να βρείτε ωραιότερα υπάρχουν ευκαιρίες
Ονόματα για τζέντλεμεν και άλλα γιά κυρίες
Ας πούμε, Πλάτων, Άδμητος, Ηλέκτρα, Ευρυάλη
Μα όλα αυτά είναι κοινά, και θα τα έχουν κι άλλοι.
Μιά Γάτα όμως, να ξέρετε, θέλει και το δικό της
Το δεύτερο το όνομα το αποκλειστικό της!
Για να μπορεί αφ΄υψηλού τον κόσμο να κοιτάει
Κια την ουρά της πάντοτε ψηλά να την κρατάει.
Πρέπει να είναι όνομα μονάχα για μιά Γάτα:
Χουρχούρης, γιά παράδειγμα, Γλείψος, Χνουδοπατάτα
Κι άλλα πολλά τέτοιας λογής μπορώ να αναφέρω:
Μπομπαλουρίνα, Πιρπιρής, Φρουφρόυ, Τρελοκαμπέρω.
Πέρα όμως απ΄αυτά τα δυό, υπάρχει κι ένα άλλο
Τ΄όνομα το μοναδικό, το τρίτο, το μεγάλο:
Το όνομα το μυστικό, ΠΟΥ ΑΝΘΡΩΠΟΣ ΔΕΝ ΞΕΡΕΙ
Και Γάτα σ΄ άνθρωπο μπροστά ποτέ δεν αναφέρει.
Όταν σε διαλογισμό λοιπόν μια Γάτα δείτε
Πάντα ο λόγος είν’ αυτός, και να το θυμηθείτε:
Σ΄απύθμενους συλλογισμούς βρίσκεται βυθισμένη
Για τ΄όνομα το άρρητο
Το αρρητορητονιάρρρητο
Το όνομά της το κρυφό σκέπτεται μαγεμένη.
Αυτή είνα η -εξαιρετική κατά τη γνώμη μου- απόδοση στα ελληνικά του»Τhe Naming of the Cats» του Έλιοτ.
The Naming Of Cats by T. S. Eliot
The Naming of Cats is a difficult matter,
It isn’t just one of your holiday games;
You may think at first I’m as mad as a hatter
When I tell you, a cat must have THREE DIFFERENT NAMES.
First of all, there’s the name that the family use daily,
Such as Peter, Augustus, Alonzo or James,
Such as Victor or Jonathan, George or Bill Bailey–
All of them sensible everyday names.
There are fancier names if you think they sound sweeter,
Some for the gentlemen, some for the dames:
Such as Plato, Admetus, Electra, Demeter–
But all of them sensible everyday names.
But I tell you, a cat needs a name that’s particular,
A name that’s peculiar, and more dignified,
Else how can he keep up his tail perpendicular,
Or spread out his whiskers, or cherish his pride?
Of names of this kind, I can give you a quorum,
Such as Munkustrap, Quaxo, or Coricopat,
Such as Bombalurina, or else Jellylorum-
Names that never belong to more than one cat.
But above and beyond there’s still one name left over,
And that is the name that you never will guess;
The name that no human research can discover–
But THE CAT HIMSELF KNOWS, and will never confess.
When you notice a cat in profound meditation,
The reason, I tell you, is always the same:
His mind is engaged in a rapt contemplation
Of the thought, of the thought, of the thought of his name:
His ineffable effable
Effanineffable
Deep and inscrutable singular Name.
Μιας και δεν έχω πολλά να πω επί της μαθηματικης ουσίας, εμπνεύστηκα από το 14. σχόλιο του Μιχάλη και τα γατιά του. 🙂
Kαι -διάολε!- να μην μπορώ να θυμηθώ ποιος μαθηματικός είπε: «Μαθηματικά είναι να δίνεις διαφορετικά ονόματα σε ίδια πράγματα.»
(νομίζω ο Πουανκαρέ…)
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Σεπτεμβρίου, 2015 @ 8:08 πμ
15. Ή μήπως ήταν : «Mαθηματικά είναι να δίνεις ίδια ονόματα σε διαφορετικά πράγματα»…?!? 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Σεπτεμβρίου, 2015 @ 8:11 πμ
Παρντόν για την παράλειψη στο 14.
Η εξαιρετική απόδοση του εγχειρίδιου πρακτικής γατικής στα ελληνικά είναι της Παυλίνας Παμπούδη
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Σεπτεμβρίου, 2015 @ 8:15 πμ
15, 16, 17: Απολαυστικό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Σεπτεμβρίου, 2015 @ 8:40 πμ
Υπόδειξη για το ερώτημα στο 12:
Προσπαθείστε να φτιάξετε τις της μορφής
της μορφής  και
και  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Σεπτεμβρίου, 2015 @ 12:55 πμ
Ήθελε αρκετή εξυπνάδα θα ομολογήσω (μια γάτα, ίσως χωρίς όνομα, αλλά με ιδιότητα) 🙂
Αν η F(x) έχει ελάχιστη περίοδο 2, η H(x) 5 και η G(x) 3 (όλες ανά δύο πρώτες μεταξύ τους), τότε η f(x)=F(X)+H(x) έχει ελάχιστη περίοδο 2*5=10 και η g(x)=G(x)-H(x) ελάχιστη περίοδο 5*3=15.
Η f(x)+g(x) = F(x)+G(x) έχει ελάχιστη περίοδο 2*3=6.
Νομίζω πάντως ότι για πρώτη ύλη θα μας έκαναν και οι τριγωνομετρικές (x σε μοίρες): F(x)=ημ(180x), H(x)=ημ(72x), G(x)=ημ(120x)
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 18 Σεπτεμβρίου, 2015 @ 9:01 πμ
20: Πολύ σωστά.
Όμως απομένει ακόμη λίγη δουλειά γιατί, στη γενική περίπτωση, τα μεγέθη δεν είναι «τόσο πρώτα μεταξύ τους».
Πιο συγκεκριμένα, αν είναι οι ελάχιστες περίοδοι των
οι ελάχιστες περίοδοι των  , και αν συμβολίσουμε με
, και αν συμβολίσουμε με 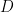 το ΜΚΔ των
το ΜΚΔ των  , τότε γράφουμε
, τότε γράφουμε
Αυτό όμως δε συνεπάγεται ότι ta ή τα
ή τα  είναι μεταξύ τους πρώτα (όπως στο παράδειγμα με τα 2, 3, 5 να παίζουν τον ρόλο των
είναι μεταξύ τους πρώτα (όπως στο παράδειγμα με τα 2, 3, 5 να παίζουν τον ρόλο των  ).
).
Σε αυτή την περίπτωση δε μπορούμε να επικαλεστούμε την εύκολη εκδοχή του προβλήματος (όπου οι ελάχιστες περίοδοι είναι μεταξύ τους πρώτες) για να ισχυριστούμε ότι η ελάχιστη περίοδος της είναι
είναι  . Αυτό δεν ισχύει για όλες τις
. Αυτό δεν ισχύει για όλες τις  με ελάχιστες περιόδους τις
με ελάχιστες περιόδους τις  . Θα πρέπει να επιλέξουμε κατάλληλες
. Θα πρέπει να επιλέξουμε κατάλληλες  για να δουλέψει το παράδειγμά μας.
για να δουλέψει το παράδειγμά μας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Σεπτεμβρίου, 2015 @ 9:56 μμ
Για να το κάνω πιο συγκεκριμένο, ας επαναλάβω την νεότερη εκδοχή του ερωτήματος 12 παραπάνω:
Μπορείτε να βρείτε δύο συναρτήσεις με ελάχιστες περιόδους
με ελάχιστες περιόδους  και
και  αντίστοιχα, τέτοιες ώστε η συνάρτηση
αντίστοιχα, τέτοιες ώστε η συνάρτηση  να έχει ελάχιστη περίοδο 6 = ΕΚΠ(60, 150 / ΜΚΔ(60, 150);
να έχει ελάχιστη περίοδο 6 = ΕΚΠ(60, 150 / ΜΚΔ(60, 150);
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Σεπτεμβρίου, 2015 @ 10:07 μμ
Να παρατηρήσω καταρχάς ότι ΕΚΠ(60,150)=300, ΜΚΔ(60,150)=30 και ΕΚΠ(60,150)/ΜΚΔ(60,150)=10 (όχι 6). Θέλουμε δηλαδή να φτιάξουμε, αν είναι δυνατόν, από συναρτήσεις f με ελάχιστη περίοδο 60 και g με ελάχιστη περίοδο 150, συνάρτηση f+g που να έχει ελάχιστη περίοδο 10=2*5.
Παρατηρώντας ότι ο ΜΚΔ(60,150)=30 είναι πολλαπλάσιος και του 2 και του 5, συμπεραίνω ότι αν δοκιμάζαμε την ίδια ακριβώς συνταγή, με οποιεσδήποτε συναρτήσεις F, H, G ελαχίστων περιόδων 2, 30, 5 αντιστοίχως δεν θα μπορούσαν ούτε οι f=F+H και g=G-H να έχουν ελάχιστες περιόδους 60 και 150 αντιστοίχως, αφού το ΕΚΠ(2,30)=ΕΚΠ(5,30)=30, μικρότερο και από το 60 και από το 150, είναι περίοδος τόσο της f όσο και της g.
Αν είναι έτσι, τότε θα πρέπει να αλλάξουμε τη συνταγή, χρησιμοποιώντας ενδεχομένως περισσότερα και διαφορετικά υλικά κατασκευής, δηλαδή συναρτήσεις F, H, G… και θα χρειαστεί ίσως νέα υπόδειξη :-).
Νομίζω πάντως ότι με τα ήδη γνωστά υλικά μπορούμε να φτιάξουμε σίγουρα τις f και g με ελάχιστες περιόδους 60 και 150 αντιστοίχως και την f+g με ελάχιστη περίοδο μικρότερη από το ΕΚΠ(60,150)=300, ως εξής:
Έστω ότι έχουμε τις F,H,G με ελάχιστες περιόδους 20, 3, 50 αντιστοίχως. Τότε η f=F+H έχει ελάχιστη περίοδο 60 (αφού οι 20 και 3 είναι σχετικά πρώτοι), η g=G-H έχει ελάχιστη περίοδο 150 (αφού οι 3 και 50 είναι σχετικά πρώτοι) και η f+g =F+G έχει ελάχιστη περίοδο το πολύ το ΕΚΠ(20,50)=100<300.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 22 Σεπτεμβρίου, 2015 @ 2:34 μμ
Μια λυση στην περιπτωση οπου εχουμε δυο περιοδους α και β, για τις οποιες, αν ε=ΕΚΠ/ΜΚΔ, τοτε το ε δεν ειναι πολλαπλασιο ουτε του α ουτε του β:
Εστω λοιπον τετοιοι φυσικοι αριθμοι α και β, και εστω $u_1$ και $u_2$ τα υπολοιπα της διαιρεσης του α και του β με το ε αντιστοιχα. Απο την υποθεση μας ειναι μη μηδενικα. Εστω $f(n)=nu_2$ για $n\in \{0,1,2,…,a\}$ και $g(n)=-nu_1$, $n\in \{0,1,2,…,b\}$ , επεκτεινοντας τες περιοδικα σε ολους τους ακεραιους. Εχουμε $f(n+u_1)-f(n)=g(n)-g(n+u_2)=u_1*u_2$, αρα $f(n+\epsilon)+g(n+\epsilon)=f(n+ca+u_1)+g(n+db+u_2)=f(n+u_1)+g(n+u_2)=f(n)+g(n)$, αρα οντως το ε ειναι περιοδος, και απο τις προηγουμενες παρατηρησεις στα σχολια πρεπει να ειναι η ελαχιστη.
Εαν απο την αλλη καποιο απο τα α και β διαιρει το ε, το ε μπορει να ειναι ελαχιστη περιοδος μονο εαν και τα δυο διαιρουν το ε. Αυτο γιατι αν α|ε, αρα το ε ειναι περιοδος της $φ$ και το ε ειναι περιοδος της $f+g$, το ε πρεπει να ειναι και περιοδος της $g$, αρα β|ε. Η περιπτωση αυτη νομιζω πως δεν μπορει να συμβαινει με α και β οχι πρωτους μεταξυ τους, και αν ισχυει αυτο τοτε σε αυτη την περιπτωση το ε δεν μπορει να ειναι ελαχιστη περιοδος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 5 Φεβρουαρίου, 2016 @ 7:10 πμ
Τι πρεπει να κανω για να γραψω latex?
Επισης, τα u_1 και u_2 πανω ειναι τα υπολοιπα της διαιρεσης του ε με το α και β αντιστοιχα, οχι το αναποδο που γραφω κατα λαθος
και τα συνολα στη δευτερη παραγραφο πρεπει να ξεκιναν απο το 1 οχι απο το 0.
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 5 Φεβρουαρίου, 2016 @ 7:16 πμ
Βασικα, αν α|ε και β|ε, τοτε για καθε πρωτο p παραγοντα του α, αν εμφανιζεται n_1>0 φορες στο α και n_2>=0 στο β, τοτε στο ε πρεπει να εμφανιζεται |n1-n2| φορες. Αυτο σημαινει πως min(n_1,n_2)=0, γιατι πρεπει στο ε να εμφανιζεται τουλαχιστον max(n_1,n_2) φορες εαν θελουμε το ε να διαιρειται και απο το α και απο το β. Αυτο σημαινει πως n_2=0. Αρα συμπεραινουμε πως αν α|ε και β|ε, τοτε α και β ειναι πρωτοι μεταξυ τους. Αρα καταληγουμε πως για α και β μη πρωτους μεταξυ τους, υπαρχει ζευγος μιας α περιοδικης και μιας β περιοδικης συναρτησης για το οποιο το ε=ΕΚΠ/ΜΚΔ ειναι ελαχιστη περιοδος του αθροισματος τους εαν και μονο εαν τα α και β δε διαιρουν το ε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 5 Φεβρουαρίου, 2016 @ 7:33 πμ
25. «Τι πρεπει να κανω για να γραψω latex?»
Γράφεις Δολάριοlatex (αφήνεις ένα κενο-space) την μαθ.έκφραση και δολάριο ξανά στο τέλος.
Π.χ ** e^(i*pi)+1=0* αντικαθιστάς τα αστέρια με δολάριο,latex,δολάριο από αριστερά προς δεξιά αντίστοιχα, και βγαίνει
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 5 Φεβρουαρίου, 2016 @ 5:52 μμ
25: Για latex δες το https://en.support.wordpress.com/latex/
Σχόλια για τα μαθηματικά θα κάνω αύριο γιατί απόψε ταξίδευα και είναι λίγο αργά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Φεβρουαρίου, 2016 @ 1:10 πμ
24: Μια πρώτη παρατήρηση είναι ότι η σχέση που γράφεις δεν ισχύει πάντα αλλά μόνο όταν τα
που γράφεις δεν ισχύει πάντα αλλά μόνο όταν τα  είναι στο ίδιο διάστημα μήκους
είναι στο ίδιο διάστημα μήκους  με αρχή πολλαπλάσιο του
με αρχή πολλαπλάσιο του  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Φεβρουαρίου, 2016 @ 1:04 μμ
Εχεις δικιο. Το δευτερο επιχειρημα ισχυει, αν το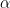 ή το
ή το 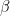 διαιρουν το
διαιρουν το  , τοτε το
, τοτε το  δεν μπορει να ειναι περιοδος. Απο την αλλη, αν τα
δεν μπορει να ειναι περιοδος. Απο την αλλη, αν τα 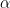 και
και 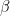 δε διαιρουν το
δε διαιρουν το  , τοτε πρεπει
, τοτε πρεπει  , και η
, και η 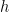 πρεπει να ειναι ΜΚΔ(α,β) περιοδική.
πρεπει να ειναι ΜΚΔ(α,β) περιοδική.
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 7 Φεβρουαρίου, 2016 @ 1:54 μμ
Δεν ειμαι σιγουρος αν στη συγκεκριμενη περιπτωση του προβληματος που τεθηκε (για περιοδους 60 και 150, το αθροισμα να εχει περιοδο 10) υπαρχει λυση. Αν οι παρατηρησεις μου στο σχολιο (30) ειναι σωστες, τοτε αφου και το υπολοιπο της διαιρεσης του e με το a ειναι
και το υπολοιπο της διαιρεσης του e με το a ειναι  , θα πρεπει να υπαρχει συναρτηση
, θα πρεπει να υπαρχει συναρτηση 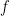 με ελαχιστη περιοδο 60 ωστε η συναρτηση
με ελαχιστη περιοδο 60 ωστε η συναρτηση  να εχει περιοδο 30. Αυτο σημαινει πως θα πρεπει
να εχει περιοδο 30. Αυτο σημαινει πως θα πρεπει  (modulo 60 παντα), δηλαδη εχουμε το συστημα
(modulo 60 παντα), δηλαδη εχουμε το συστημα 
Αυτο το συστημα ομως εχει μονο τη λυση (το οποιο φαινεται ευκολα αφαιροντας πρωτα τις 2 πρωτες εξισωσεις και μετα συγκρινοντας την εξισωση που προεκυψε με την τριτη). Επειδη αναλογες λυσεις εχουμε και για τις αλλες κλασεις ισοδυναμιας που οριζονται πανω στην
(το οποιο φαινεται ευκολα αφαιροντας πρωτα τις 2 πρωτες εξισωσεις και μετα συγκρινοντας την εξισωση που προεκυψε με την τριτη). Επειδη αναλογες λυσεις εχουμε και για τις αλλες κλασεις ισοδυναμιας που οριζονται πανω στην  παιρνουμε πως
παιρνουμε πως  (n modulo 60 παντα) το οποιο αντιφασκει με το γεγονος πως η ελαχιστη περιοδος της
(n modulo 60 παντα) το οποιο αντιφασκει με το γεγονος πως η ελαχιστη περιοδος της  ειναι 60.
ειναι 60.
Μου αρέσει!Αρέσει σε 1 άτομο
Σχόλιο από reddove — 7 Φεβρουαρίου, 2016 @ 8:15 μμ
30,31: Μπορείς να τα γράψεις λίγο καλύτερα αυτά στο 30 γιατί δεν τα καταλαβαίνω;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 8 Φεβρουαρίου, 2016 @ 1:29 πμ
Ελπιζω να τα εχω γραψει λιγοτερο μπερδεμενα. Θα ξεκινησω απο την αρχη, χωρις να αναφερθω στα υπολοιπα σχόλιά μου. Το δευτερο κομματι του σχολιου μου 30) αναφερομαι στο οτι , και αρα η
, και αρα η 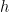 ειναι
ειναι  και
και  περιοδικη (αφου η
περιοδικη (αφου η  ειναι a-περιοδικη και η
ειναι a-περιοδικη και η  b-περιοδικη), αρα πρεπρει να ειναι ΜΚΔ(a,b) περιοδικη. Αυτο με μια επιχειρηματολογια αναλογη της επιχειρηματολογιας μου στο 31) νομιζω πως δινει μια αποδειξη για αυτα που θα πραοσπαθησω να δειξω στη συνεχεια με εναν αλλο τροπο, αλλα νομιζω πως ειναι πολυ πιο τεχνικη και ακομψη, οποτε δεν μπηκα στον κοπο να την καθαρογραψω.
b-περιοδικη), αρα πρεπρει να ειναι ΜΚΔ(a,b) περιοδικη. Αυτο με μια επιχειρηματολογια αναλογη της επιχειρηματολογιας μου στο 31) νομιζω πως δινει μια αποδειξη για αυτα που θα πραοσπαθησω να δειξω στη συνεχεια με εναν αλλο τροπο, αλλα νομιζω πως ειναι πολυ πιο τεχνικη και ακομψη, οποτε δεν μπηκα στον κοπο να την καθαρογραψω.
Εστω περιοδικές με ελάχιστες περιόδους
περιοδικές με ελάχιστες περιόδους  αντιστοιχα. Έστω ε=ΕΚΠ(a,b)/ΜΚΔ(a,b) και μ=ΜΚΔ(a,b). Έστω
αντιστοιχα. Έστω ε=ΕΚΠ(a,b)/ΜΚΔ(a,b) και μ=ΜΚΔ(a,b). Έστω  .
.
1) Ισχυρίζομαι πως αν και αν ενα απο τα δύο διαιρει το
και αν ενα απο τα δύο διαιρει το  , τότε το
, τότε το  δεν μπορεί να είναι περίοδος της
δεν μπορεί να είναι περίοδος της  . Εστω πχ πως το
. Εστω πχ πως το  διαιρεί το
διαιρεί το  , και οτι το
, και οτι το  ειναι περίοδος της
ειναι περίοδος της 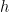 . Τοτε το
. Τοτε το  ειναι περιοδος της
ειναι περιοδος της  . Άρα είναι επίσης περίοδος της
. Άρα είναι επίσης περίοδος της  , που εχει ελαχιστη περιοδο
, που εχει ελαχιστη περιοδο  , αρα
, αρα  . Εάν όμως τα
. Εάν όμως τα  και
και  δεν ειναι πρωτα μεταξυ τους, εχουμε
δεν ειναι πρωτα μεταξυ τους, εχουμε  ,
,  ,
,  και
και  . Αν
. Αν  , τοτε
, τοτε  και αντιστοιχα το
και αντιστοιχα το  , δινει
, δινει  , που σημαινει πως τα
, που σημαινει πως τα 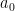 και
και 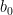 εχουν κοινο παραγοντα το
εχουν κοινο παραγοντα το 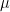 που όμως ειναι ατοπο (γιατι το μ ειναι ο ΜΚΔ των a και b, και αυτο που βρηκαμε ειναι πως το
που όμως ειναι ατοπο (γιατι το μ ειναι ο ΜΚΔ των a και b, και αυτο που βρηκαμε ειναι πως το  διαιρει τα
διαιρει τα  και
και  .)
.)
2) Ενας αλλος τροπος να το δουμε είναι πως αν ειναι ενας πρωτος παραγοντας του
ειναι ενας πρωτος παραγοντας του  , που εμφανιζεται
, που εμφανιζεται  φορες στο
φορες στο  και
και 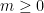 στο
στο  , τοτε εμφανιζεται
, τοτε εμφανιζεται  φορες στο
φορες στο 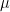 και
και  φορες στο
φορες στο  , ενώ στο
, ενώ στο  εμφανιζεται
εμφανιζεται  φορες. Αρα αν
φορες. Αρα αν  και
και  τοτε
τοτε  που σημαινει πως
που σημαινει πως 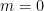 . Άρα σε τετοια περίπτωση τα a και b πρεπει να ειναι μεταξυ τους πρωτοι.
. Άρα σε τετοια περίπτωση τα a και b πρεπει να ειναι μεταξυ τους πρωτοι.
3) Η ιδια επιχειρηματολογια μπορει ακριβως να εφαρμοστει αν για περιοδο της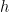 παρουμε ενα πολλαπλασιο
παρουμε ενα πολλαπλασιο  ,
,  και υποθεσουμε πως
και υποθεσουμε πως  . Πάλι με την ιδια επιχειρηματολογια
. Πάλι με την ιδια επιχειρηματολογια  και αυτο σημαινει πως καθε πρωτος παραγοντας των
και αυτο σημαινει πως καθε πρωτος παραγοντας των  πρεπει να εμφανιζεται στο
πρεπει να εμφανιζεται στο  με τη μεγιστη συχνοτητα που εμφανιζεται στα
με τη μεγιστη συχνοτητα που εμφανιζεται στα  . Αυτο δινει πως αν
. Αυτο δινει πως αν  και
και  (και
(και  ) τοτε η ελαχιστη περιοδος πρεπει να ειναι τουλαχιστον ιση με
) τοτε η ελαχιστη περιοδος πρεπει να ειναι τουλαχιστον ιση με  .
.
4) Αυτο το τελευταιο στην πραγματικοτητα μας δινει κατι γενικοτερο. Κατα αρχας ας παρατηρησουμε πως αν και
και  , οπου το
, οπου το  ειναι ενας ακεραιος που δε διαιρειται απο κανενα
ειναι ενας ακεραιος που δε διαιρειται απο κανενα  , δηλαδη στο
, δηλαδη στο  εχουμε συγκεντρωσει ολους τους πρωτους παραγοντες που εμφανιζονται στα
εχουμε συγκεντρωσει ολους τους πρωτους παραγοντες που εμφανιζονται στα  και
και  με την ιδια ακριβως συχνοτητα, τοτε αν
με την ιδια ακριβως συχνοτητα, τοτε αν 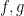 εχουν περιοδους
εχουν περιοδους  αντιστοιχα, και η
αντιστοιχα, και η 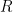 εχει περιοδο
εχει περιοδο  , τοτε οι
, τοτε οι  εχουν περιοδους
εχουν περιοδους  και
και  αντιστοιχα, και
αντιστοιχα, και  , αρα στο προβλημα του να βρουμε συναρτησεις με περιοδους
, αρα στο προβλημα του να βρουμε συναρτησεις με περιοδους  τετοιες ωστε να εχουν τη μικροτερη δυνατη ελαχιστη περιοδο, μπορουμε χωρις βλαβη της γενικοτητας να υποθεσουμε πως
τετοιες ωστε να εχουν τη μικροτερη δυνατη ελαχιστη περιοδο, μπορουμε χωρις βλαβη της γενικοτητας να υποθεσουμε πως  , δηλαδη πως καθε πρωτος παραγοντας εμφανιζεται με διαφορετικες συχνοτητες στα
, δηλαδη πως καθε πρωτος παραγοντας εμφανιζεται με διαφορετικες συχνοτητες στα  .
.
5) Εστω λοιπον και
και  ,
,  . Τοτε,
. Τοτε,  και
και  . Έστω
. Έστω  . Μπορουμε να βρουμε
. Μπορουμε να βρουμε 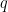 τετοιο ωστε
τετοιο ωστε  ή
ή  αλλα
αλλα  : το q να «συμπληρωνει» καποιους πρωτους παραγοντες στο
: το q να «συμπληρωνει» καποιους πρωτους παραγοντες στο  . Πραγματι αυτο γινεται γιατι υπαρχει
. Πραγματι αυτο γινεται γιατι υπαρχει 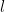 ωστε
ωστε  . Ας πουμε πχ πως για αυτο το
. Ας πουμε πχ πως για αυτο το 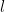 ισχυει πως
ισχυει πως  . Τοτε μπορουμε να παρουμε για
. Τοτε μπορουμε να παρουμε για 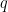 το γινομενο
το γινομενο  και τοτε οντως
και τοτε οντως  και
και  . Αυτο ομως με βαση το 3) ειναι ατοπο, καθως τοτε θα ειχαμε πως
. Αυτο ομως με βαση το 3) ειναι ατοπο, καθως τοτε θα ειχαμε πως  (αν ειχαμε
(αν ειχαμε  τοτε θα παιρναμε
τοτε θα παιρναμε  αρχικα και αυτο θα μας εδινε μετα το
αρχικα και αυτο θα μας εδινε μετα το  ) αλλά όπως κατασκευάσαμε το
) αλλά όπως κατασκευάσαμε το 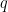 έχουμε πως το
έχουμε πως το  εμφανιζεται στο
εμφανιζεται στο  μια φορα παραπανω απο οτι στο
μια φορα παραπανω απο οτι στο  , αρα
, αρα  . Αυτο σημαινει πως το
. Αυτο σημαινει πως το  δεν μπορει να ειναι περιοδος της
δεν μπορει να ειναι περιοδος της  για κανενα
για κανενα  . Από την άλλη, το
. Από την άλλη, το  =ΕΚΠ(a,b) ειναι παντα περιοδος της
=ΕΚΠ(a,b) ειναι παντα περιοδος της  . Άρα, για οποιεσδηποτε συναρτησεις
. Άρα, για οποιεσδηποτε συναρτησεις 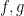 με περιοδους
με περιοδους  της μορφης
της μορφης  και
και  ,
,  , η ελαχιστη κοινη περιοδος ειναι παντα ιση με το ΕΚΠ των a και b.
, η ελαχιστη κοινη περιοδος ειναι παντα ιση με το ΕΚΠ των a και b.
6) Άρα συγκεντρωνοντας τα αποτελεσματα, εχουμε δει πως αν εχουμε δυο φυσικους και
και  και συναρτησεις
και συναρτησεις 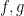 με περιοδους
με περιοδους  , τοτε η ελαχιστη περιοδος της
, τοτε η ελαχιστη περιοδος της  ειναι μεγαλυτερη ή ίση με
ειναι μεγαλυτερη ή ίση με  . Εάν
. Εάν  για κάθε
για κάθε  , τοτε η ελαχιστη περιοδος της
, τοτε η ελαχιστη περιοδος της  ειναι παντα ακριβως αυτη. Επίσης για κάθε
ειναι παντα ακριβως αυτη. Επίσης για κάθε  υπαρχουν συναρτησεις
υπαρχουν συναρτησεις 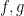 με
με  για περιοδους ώστε η ελαχιστη περιοδος της
για περιοδους ώστε η ελαχιστη περιοδος της  να ειναι η μικροτερη δυνατη, δηλαδη
να ειναι η μικροτερη δυνατη, δηλαδη  . Γενικα, μπορουμε παντα να κατασκευασουμε
. Γενικα, μπορουμε παντα να κατασκευασουμε 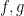 με περιοδους
με περιοδους  ωστε η
ωστε η  να εχει ελαχιστη περιοδο
να εχει ελαχιστη περιοδο  για οποιοδηποτε συνολο στοιχειων
για οποιοδηποτε συνολο στοιχειων  επιλεξουμε.
επιλεξουμε.
Δημητρης
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 8 Φεβρουαρίου, 2016 @ 4:58 πμ
Και ενα συμπληρωμα στο (6): Βασικα, μπορουμε παντα να κατασκευασουμε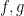 με περιοδους
με περιοδους  ωστε η
ωστε η  να εχει ελαχιστη περιοδο
να εχει ελαχιστη περιοδο  για οποιοδηποτε συνολο στοιχειων
για οποιοδηποτε συνολο στοιχειων  και επιλογες
και επιλογες  (αφου καθε
(αφου καθε  -περιοδικη συναρτηση ειναι προφανως και
-περιοδικη συναρτηση ειναι προφανως και  περιοδικη,
περιοδικη,  ). Αυτες ειναι ολες οι δυνατες ελαχιστες περιοδοι που μπορουν να υπαρξουν, για την ακριβεια. Κατασκευη αυτων των συναρτησεων μπορει να γινει προσθετωντας στις f και g τις συναρτησεις με τις περιοδους που θελουμε και προσθαφαιρωντας αυτες που θελουμε να εξαλειψουμε, οπως στην παραγραφο 4).
). Αυτες ειναι ολες οι δυνατες ελαχιστες περιοδοι που μπορουν να υπαρξουν, για την ακριβεια. Κατασκευη αυτων των συναρτησεων μπορει να γινει προσθετωντας στις f και g τις συναρτησεις με τις περιοδους που θελουμε και προσθαφαιρωντας αυτες που θελουμε να εξαλειψουμε, οπως στην παραγραφο 4).
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 8 Φεβρουαρίου, 2016 @ 5:11 πμ
Θα προσπαθησω να μεταφρασω αυτο που εγραψα: Εχουμε δειξει πως αν η ελαχιστη περιοδος της f διαιρει μια περιοδο της f+g τοτε και η ελαχιστη περιοδος της g θα πρεπει να διαιρει την περιοδο της f+g (αυτο ειναι γιατι μπορουμε να γραψουμε αρα η περιοδος της f+g, που ειναι και περιοδος της f αφου η ελαχιστη περιοδος της τη διαιρει, πρεπει να ειναι και περιοδος της g). Αλλα αν και καμια απο τις δυο ελαχιστες περιοδους διαιρει εναν αριθμο που εχουμε ως υποψηφια περιοδο του αθροισματος, μπορουμε πολλες φορες να βρουμε ενα πολλαπλασιο αυτου του αριθμου, το οποιο επισης πρεπει να ειναι περιοδος αν ο ιδιος ο αριθμος ειναι, το οποιο να διαιρειται ακριβως απο μονο μια απο τις δυο ελαχιστες περιοδους. Ο μικροτερος αριθμος για τον οποιο αυτο δεν μπορει να συμβει, δηλαδη για τον οποιο καθε πολλαπλασιο που διαιρειται απο εναν αριθμο, να πρεπει να διαιρειται και απο τον αλλο, ειναι αυτος που ειναι ο μονος πραγματικα υποψηφιος για ελαχιστη περιοδος του αθροισματος. Αυτος ο αριθμος, ας τον πουμε Ν, ειναι ακριβως το γινομενο των πρωτων παραγοντων των ελαχιστων περιοδων, υψωμενων στην μεγαλυτερη δυναμη που εμφανιζονται, αλλα χωρις αυτους τους αριθμους που εμφανιζονται με ακριβως την ιδια δυναμη στις ελαχιστες περιοδους, και αυτο ειναι γιατι, αφου εμφανιζονται με την ιδια δυναμη και στις δυο ελαχιστες περιοδους, καθε πολλαπλασιο του Ν ειτε θα διαιρειται και απο τους δυο αριθμους, δηλαδη θα περιεχει ολες αυτες τις δυναμεις, ειτε δε θα διαιρειται απο κανεναν απο τους δυο, δηλαδη καποια δυναμη θα υπολειπεται. Αρα αυτος ο αριθμος ειναι η μικροτερη υποψηφια περιοδος και πραγματι μπορει να κατασκευαστουν καταλληλες τετοιες συναρτησεις με τον τροπο με τα αθροισματα που ειχε αναφερθει στο σχολιο 21.
αρα η περιοδος της f+g, που ειναι και περιοδος της f αφου η ελαχιστη περιοδος της τη διαιρει, πρεπει να ειναι και περιοδος της g). Αλλα αν και καμια απο τις δυο ελαχιστες περιοδους διαιρει εναν αριθμο που εχουμε ως υποψηφια περιοδο του αθροισματος, μπορουμε πολλες φορες να βρουμε ενα πολλαπλασιο αυτου του αριθμου, το οποιο επισης πρεπει να ειναι περιοδος αν ο ιδιος ο αριθμος ειναι, το οποιο να διαιρειται ακριβως απο μονο μια απο τις δυο ελαχιστες περιοδους. Ο μικροτερος αριθμος για τον οποιο αυτο δεν μπορει να συμβει, δηλαδη για τον οποιο καθε πολλαπλασιο που διαιρειται απο εναν αριθμο, να πρεπει να διαιρειται και απο τον αλλο, ειναι αυτος που ειναι ο μονος πραγματικα υποψηφιος για ελαχιστη περιοδος του αθροισματος. Αυτος ο αριθμος, ας τον πουμε Ν, ειναι ακριβως το γινομενο των πρωτων παραγοντων των ελαχιστων περιοδων, υψωμενων στην μεγαλυτερη δυναμη που εμφανιζονται, αλλα χωρις αυτους τους αριθμους που εμφανιζονται με ακριβως την ιδια δυναμη στις ελαχιστες περιοδους, και αυτο ειναι γιατι, αφου εμφανιζονται με την ιδια δυναμη και στις δυο ελαχιστες περιοδους, καθε πολλαπλασιο του Ν ειτε θα διαιρειται και απο τους δυο αριθμους, δηλαδη θα περιεχει ολες αυτες τις δυναμεις, ειτε δε θα διαιρειται απο κανεναν απο τους δυο, δηλαδη καποια δυναμη θα υπολειπεται. Αρα αυτος ο αριθμος ειναι η μικροτερη υποψηφια περιοδος και πραγματι μπορει να κατασκευαστουν καταλληλες τετοιες συναρτησεις με τον τροπο με τα αθροισματα που ειχε αναφερθει στο σχολιο 21.
Μου αρέσει!Μου αρέσει!
Σχόλιο από reddove — 8 Φεβρουαρίου, 2016 @ 1:52 μμ
33-35: Τέλεια. Μάλλον δεν άφησες τίποτα που να μην το ξεκαθαρίσεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Φεβρουαρίου, 2016 @ 11:03 μμ