Έστω ο γραμμικός χώρος όλων των πραγματικών ακολουθιών
με
.
Ο γραμμικός χώρος είναι και μετρικός με τη μετρική
. Ορίζουμε τη γραμμική απεικόνιση
(σπρώχνουμε όλες τις συντεταγμένες του διανύσματος μία θέση προς τα αριστερά και μετά τις πολλαπλασιάζουμε όλες επί 2).
Δείξτε ότι υπάρχει διάνυσμα τέτοιο ώστε το σύνολο (τροχιά)
να είναι πυκνό στον , δηλ. για κάθε σημείο
υπάρχει υπακολουθία της τροχιάς του
που συγκλίνει στο
.
Υπόδειξη:
Ο χώρος έχει αριθμήσιμο πυκνό υποσύνολο με τη μετρική που περιγράφουμε. Για παράδειγμα το σύνολο όλων των ακολουθιών που είναι (α) τελικά μηδενικές και (β) έχουν ρητά στοιχεία, είναι και αριθμήσιμο και πυκνό όπως εύκολα μπορεί κανείς να αποδείξει. Αρκεί λοιπόν να βρεθεί ένα
έχει αριθμήσιμο πυκνό υποσύνολο με τη μετρική που περιγράφουμε. Για παράδειγμα το σύνολο όλων των ακολουθιών που είναι (α) τελικά μηδενικές και (β) έχουν ρητά στοιχεία, είναι και αριθμήσιμο και πυκνό όπως εύκολα μπορεί κανείς να αποδείξει. Αρκεί λοιπόν να βρεθεί ένα 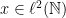 του οποίου η τροχιά να προσεγγίζει όλα τα στοιχεία του πυκνού υποσυνόλου οσοδήποτε καλά.
του οποίου η τροχιά να προσεγγίζει όλα τα στοιχεία του πυκνού υποσυνόλου οσοδήποτε καλά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 3 Αυγούστου, 2010 @ 4:46 μμ
Συμβολίζω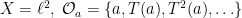 και
και 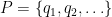 το πυκνό σύνολο που αναφέρετε. Έστω
το πυκνό σύνολο που αναφέρετε. Έστω  ανοικτά,
ανοικτά,  και
και 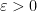 έτσι ώστε
έτσι ώστε  . Αν
. Αν 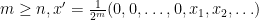 με
με  μηδενικά στην αρχή και το
μηδενικά στην αρχή και το  αρκετά μεγάλο έτσι ώστε
αρκετά μεγάλο έτσι ώστε 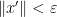 τότε
τότε 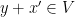 και
και  .
. ανοικτό, το σύνολο
ανοικτό, το σύνολο  είναι πυκνό στον
είναι πυκνό στον 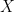 .
. . Αφού ο
. Αφού ο 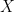 είναι πλήρης μετρικός χώρος από το θεώρημα baire το
είναι πλήρης μετρικός χώρος από το θεώρημα baire το  είναι πυκνό στον
είναι πυκνό στον 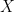 . Κάθε στοιχείο του
. Κάθε στοιχείο του 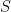 έχει πυκνή τροχιά.
έχει πυκνή τροχιά.
Άρα δείξαμε ότι αν
Έστω
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 21 Ιανουαρίου, 2011 @ 3:00 πμ
Στη τέταρτη γραμμή πρέπει να είναι .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 21 Ιανουαρίου, 2011 @ 3:03 πμ
Πολύ σωστά. (Ξέχασες μόνο να πεις ότι τα σύνολα είναι ανοιχτά.)
είναι ανοιχτά.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Ιανουαρίου, 2011 @ 11:08 μμ