Παίρνουμε μια συνηθισμένη τράπουλα (52 φύλλα σε 13 είδη, από 4 κάθε είδος), την ανακατεύουμε και την μοιράζουμε σε 13 σωρούς των 4 φύλλων.
Είναι πάντα δυνατό ή όχι να επιλέξουμε ένα φύλλο από κάθε σωρό ώστε στο τέλος να έχουμε ένα φύλλο από κάθε είδος;

Υπόδειξη:
Πρέπει για καθένα από τα 13 είδη να επιλέξετε ακριβώς έναν από τους 13 σωρούς, στον οποίο να εμφανίζεται αυτό το είδος, και από αυτό το σωρό να αφαιρέσετε ένα χαρτί αυτού του είδους.
Μπορείτε πάντα να το κάνετε αυτό; (Εννοείται πως σε διαφορετικά είδη πρέπει να αντιστοιχούν διαφορετικοί σωροί.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Απριλίου, 2010 @ 5:34 μμ
Υπόδειξη:
«Πρέπει για καθένα από τα 13 είδη να επιλέξετε ακριβώς έναν από τους 13 σωρούς…»
Παντρέψτε δηλ. τους σωρούς με τα είδη …
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Απριλίου, 2010 @ 10:10 πμ
Αν κατάλαβα σωστά το πρόβλημα, νομίζω ότι δεν είναι δυνατό να βρεθεί τρόπος επιλογής των φύλλων έτσι ώστε όπως και να γίνει το ανακάτεμα να επιλέγουμε πάντα 13 διαφορετικά είδη.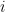 σωρό το
σωρό το 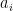 φύλλο (
φύλλο ( )»
)»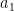 στον πρώτο σωρό και
στον πρώτο σωρό και 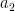 στον δεύτερο σωρό να είναι του ιδίου είδους.
στον δεύτερο σωρό να είναι του ιδίου είδους.
Αν π.χ. δώσει κάποιος τη λύση:
» Επιλέγουμε από τον
τότε μπορούμε να ανακατέψουμε τη τράπουλα με τέτοιο τρόπο έτσι ώστε τα φύλλα
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 28 Απριλίου, 2010 @ 2:50 μμ
Ο αλγόριθμος που προτείνεις είναι «τυφλός», δε λαμβάνει δηλ. υπόψιν του το πώς έχει κανείς ανακατέψει την τράπουλα και φτιάξει τους σωρούς. Όμως αυτό δεν είναι απαραίτητο. Τους σωρούς τους βλέπουμε πριν διαλέξουμε.
Εδώ φταίω μάλλον εγώ με την εικόνα που επέλεξα και που δείχνει τους σωρούς γυρισμένους προς τα κάτω.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Απριλίου, 2010 @ 3:14 μμ
Έστω ότι μετά από κάποιο ανακάτεμα διαλέξαμε από τους πρώτους σωρούς
σωρούς  διαφορετικά είδη και ότι δεν μπορούμε να διαλέξουμε άλλο είδος από τους επόμενους σωρούς. Αριθμώντας κατάλληλα τα φύλλα μας (σε ίδια είδη δίνουμε τον ίδιο αριθμό) μπορούμε να υποθέσουμε ότι επιλέξαμε το
διαφορετικά είδη και ότι δεν μπορούμε να διαλέξουμε άλλο είδος από τους επόμενους σωρούς. Αριθμώντας κατάλληλα τα φύλλα μας (σε ίδια είδη δίνουμε τον ίδιο αριθμό) μπορούμε να υποθέσουμε ότι επιλέξαμε το 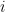 φύλλο από τον
φύλλο από τον 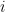 σωρό για
σωρό για 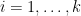 και ότι στους σωρούς
και ότι στους σωρούς  υπάρχουν μόνο φύλλα είδους
υπάρχουν μόνο φύλλα είδους  . Για να συμβαίνει αυτό πρέπει
. Για να συμβαίνει αυτό πρέπει  . Έστω ότι στον
. Έστω ότι στον 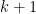 σωρό υπάρχει το φύλλο
σωρό υπάρχει το φύλλο  . Αν στον
. Αν στον  σωρό υπάρχει φύλλο είδους
σωρό υπάρχει φύλλο είδους  επιλέγουμε από τον
επιλέγουμε από τον  σωρό το φύλλο
σωρό το φύλλο 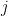 και από τον
και από τον 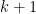 σωρό το φύλλο
σωρό το φύλλο  . Αν δεν συμβαίνει το τελευταίο τότε στον
. Αν δεν συμβαίνει το τελευταίο τότε στον  σωρό υπάρχει φύλλο είδους
σωρό υπάρχει φύλλο είδους  . Αν στον
. Αν στον  σωρό υπάρχει φύλλο είδους
σωρό υπάρχει φύλλο είδους  επιλέγουμε από τον
επιλέγουμε από τον  σωρό το φύλλο
σωρό το φύλλο 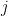 από τον
από τον  σωρό το φύλλο
σωρό το φύλλο  και από τον
και από τον 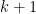 σωρό το φύλλο
σωρό το φύλλο  . Συνεχίζοντας με τον ίδιο τρόπο σίγουρα θα βρούμε φύλλο είδους
. Συνεχίζοντας με τον ίδιο τρόπο σίγουρα θα βρούμε φύλλο είδους  αφού ο μόνος τρόπος να μη συμβεί αυτό είναι να πέσουμε σε κύκλο. Δηλαδή να βρούμε αριθμούς
αφού ο μόνος τρόπος να μη συμβεί αυτό είναι να πέσουμε σε κύκλο. Δηλαδή να βρούμε αριθμούς  διαφορετικούς ανά δύο (άρα
διαφορετικούς ανά δύο (άρα  ) έτσι ώστε στους σωρούς
) έτσι ώστε στους σωρούς  να υπάρχουν μόνο φύλλα είδους
να υπάρχουν μόνο φύλλα είδους  το οποίο δεν γίνετε αφού στον
το οποίο δεν γίνετε αφού στον 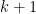 σωρό υπάρχει φύλλο είδους
σωρό υπάρχει φύλλο είδους  .
.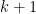 σωρούς
σωρούς 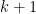 διαφορετικά είδη.
διαφορετικά είδη.
Άρα μπορούμε να διαλέξουμε από τους πρώτους
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 13 Μαΐου, 2010 @ 11:07 μμ
pamp0s:
Η ιδέα σου είναι καλή και μάλλον μπορεί να σωθεί, αλλά όπως το γράφεις δε με πείθεις εκεί που λές
Δηλ. το ότι μπορεί να κλείσεις κύκλο όπως πας δε μου φαίνεται να σημαίνει ότι οι σωροί που συμμετέχουν σε αυτόν τον κύκλο περιέχουν μόνο χαρτιά από τους σωρούς . Μπορεί απλά οι επιλογές που έκανες να ήταν εσφαλμένες.
. Μπορεί απλά οι επιλογές που έκανες να ήταν εσφαλμένες.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 14 Μαΐου, 2010 @ 10:11 πμ
Έχετε δίκαιο μπορεί οι επιλογές να ήταν εσφαλμένες. Συνεχίζω λοιπόν στο προηγούμενο σχόλιο μου. . Έστω προς άτοπο ότι σε κάθε επιλογή των
. Έστω προς άτοπο ότι σε κάθε επιλογή των  δεν βρίσκουμε φύλλο είδους
δεν βρίσκουμε φύλλο είδους  στον σωρό
στον σωρό  .
. σίγουρα θα πέσουμε σε κύκλο ( εννοώντας
σίγουρα θα πέσουμε σε κύκλο ( εννοώντας  για κάποιο
για κάποιο  και το
και το  είναι το ελάχιστο με αυτή την ιδιότητα), αφού
είναι το ελάχιστο με αυτή την ιδιότητα), αφού  . Από όλες τις δυνατές επιλογές των
. Από όλες τις δυνατές επιλογές των  έστω
έστω  όλα τα διαφορετικά ανά δύο
όλα τα διαφορετικά ανά δύο  που εμφανίζονται. Τότε από τον τρόπο επιλογής των
που εμφανίζονται. Τότε από τον τρόπο επιλογής των  στους σωρούς
στους σωρούς  υπάρχουν μόνο φύλλα είδους
υπάρχουν μόνο φύλλα είδους  το οποίο είναι αδύνατο.
το οποίο είναι αδύνατο.
…Συνεχίζοντας με τον ίδιο τρόπο σίγουρα θα βρούμε φύλλο είδους
Σε κάθε επιλογή των
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 14 Μαΐου, 2010 @ 1:08 μμ
Νομίζω πως τώρα είναι σωστό.
Όμως υπάρχει και μια άλλη λύση που χρησιμοποιεί το λεγόμενο (δείτε π.χ. εδώ για το θέωρημα αυτό), που είναι ένα πολύ εύχρηστο θεώρημα και καλό είναι να το έχει κανείς υπ’ όψιν του.
Μπορείτε να τη βρείτε;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 15 Μαΐου, 2010 @ 12:49 πμ
Έστω οι σωροί (σύνολα αριθμών που περιέχονται σε κάθε σωρό, τα χρώματα τα αγνοούμε). Τότε για κάθε
οι σωροί (σύνολα αριθμών που περιέχονται σε κάθε σωρό, τα χρώματα τα αγνοούμε). Τότε για κάθε  οι σωροί που αντιστοιχούν στους δείκτες
οι σωροί που αντιστοιχούν στους δείκτες 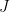 έχουν
έχουν  χαρτιά άρα τουλάχιστο
χαρτιά άρα τουλάχιστο  διαφορετικούς αριθμούς. Άρα
διαφορετικούς αριθμούς. Άρα  το οποίο είναι η συνθήκη του Hall. Άρα από το θεώρημα του Γάμου υπάρχουν
το οποίο είναι η συνθήκη του Hall. Άρα από το θεώρημα του Γάμου υπάρχουν  διαφορετικά ανά δύο το οποίο είναι το ζητούμενο.
διαφορετικά ανά δύο το οποίο είναι το ζητούμενο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 15 Μαΐου, 2010 @ 11:22 πμ
Φυσικά αριθμήσαμε τα φύλλα τυχαία (σε ίδια είδη ίδιο αριθμό) και θεωρούμε τα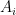 σαν σύνολα
σαν σύνολα
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 15 Μαΐου, 2010 @ 11:30 πμ
Πολύ σωστά.
Το θεώρημα του Hall είναι πάρα πολύ χρήσιμο και πρέπει κανείς να το έχει υπόψιν του μια και ξεπηδάει συχνά εκεί που δεν το περιμένεις.
Ένα άλλο πρόβλημα που έχει τοποθετηθεί σε αυτό το blog αλλά δεν έχει λυθεί ακόμη, μπορεί επίσης να λυθεί με χρήση του θεωρήματος του Hall (συν λίγη εύκολη γεωμετρία). Αυτό είχε προκύψει παλιότερα στην έρευνά μου. Πρόκειται δηλ. για «ρεαλιστικό» πρόβλημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 15 Μαΐου, 2010 @ 11:39 πμ