Έστω . Ο
είναι το άθροισμα των ψηφίων του
(στο δεκαδικό σύστημα), και ο
το άθροισμα των ψηφίων του
. Ποιό είναι το άθροισμα των ψηφίων του
;
1 Ιουνίου, 2008
Μια πολύ μεγάλη πρόσθεση
4 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Έστω D το άθροισμα των ψηφίων του Γ.
To πλήθος των ψηφίων του Β θα είναι![{}[4444\cdot \log{(4444)}]+1=16211](https://s0.wp.com/latex.php?latex=%7B%7D%5B4444%5Ccdot+%5Clog%7B%284444%29%7D%5D%2B1%3D16211&bg=ffffff&fg=000000&s=0&c=20201002) .
.![{}[\log{(16211)}]+1=5](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Clog%7B%2816211%29%7D%5D%2B1%3D5&bg=ffffff&fg=000000&s=0&c=20201002) .
.![{}[\log{(5)}]+1=1](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Clog%7B%285%29%7D%5D%2B1%3D1&bg=ffffff&fg=000000&s=0&c=20201002) .
.
To πλήθος των ψηφίων του Γ θα είναι
Άρα το πλήθος των ψηφίων του D θα είναι
Ξέρουμε επίσης ότι και βρίσκουμε ότι
και βρίσκουμε ότι
 .
.
Συνεπώς .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από steliosdes — 1 Ιουνίου, 2008 @ 9:32 μμ
Μήπως μπορείτε να τα εξηγήσετε λίγο παραπάνω αυτά; Δεν είμαι σίγουρος ότι είναι σωστό αλλά ίσως απλά να μην καταλαβαίνω πώς βρήκατε τί.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Ιουνίου, 2008 @ 3:46 μμ
Ναι έχετε δίκιο, το έγραψα βιαστικά χθες και είχα εντελώς λάθος συλλογισμό.
Η λογική είναι η εξής:
To πλήθος των ψηφίων του Α είναι![{}[4444\cdot \log(4444)]+1=16211](https://s0.wp.com/latex.php?latex=%7B%7D%5B4444%5Ccdot+%5Clog%284444%29%5D%2B1%3D16211&bg=ffffff&fg=000000&s=0&c=20201002) .
.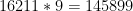 .
.![{}[\log(145899)]+1=6](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Clog%28145899%29%5D%2B1%3D6&bg=ffffff&fg=000000&s=0&c=20201002) .
. θα είναι το πολύ
θα είναι το πολύ 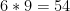 .
.
Άρα το Β θα είναι το πολύ
Οπότε το πλήθος των ψηφίων του Β θα είναι το πολύ
Δηλαδή το
Τώρα ισχύει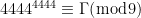 οπότε
οπότε 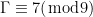 και επειδή
και επειδή  το άθροισμα των ψηφίων του θα είναι 7 άρα
το άθροισμα των ψηφίων του θα είναι 7 άρα  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από steliosdes — 2 Ιουνίου, 2008 @ 7:31 μμ
Σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Ιουνίου, 2008 @ 9:50 μμ