Ένα ορθογώνιο παραλληλεπίπεδο περιέχεται μέσα σ’ ένα άλλο ορθογώνιο παραλληλεπίπεδο. Τα δύο παραλληλεπίπεδα δεν είναι κατ’ ανάγκη παράλληλα μεταξύ τους.
Δείξτε ότι το άθροισμα των διαστάσεων του μέσα (μήκος + πλάτος + ύψος) είναι μικρότερο από το άθροισμα διαστάσεων του έξω.
Υπόδειξη:
Η επιφάνεια του μέσα ορθογωνίου είναι μικρότερη από του απ’ έξω (δείτε και αυτό το παλιότερο ερώτημα για να δείτε πώς μπορείτε να το δείξετε αυτό).
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Ιουνίου, 2008 @ 9:48 πμ
Υπόδειξης συνέχεια:
Αν είναι a,b,c οι διαστάσεις του μέσα ορθογωνίου και A,B,C οι διαστάσεις του απ’ έξω, τότε από τη σύγκριση των εμβαδών έχουμε την ανισότητα
Σκοπός σας είναι να δείξετε την ανισότητα
ή, ισοδύναμα, την .
.
Μπορείτε να βρείτε άλλη μια ανισότητα που να συνδέει τις ποσότητες a,b,c,A,B,C για να τη χρησιμοποιήσετε μαζί με την ανισότητα που προκύπτει από τη σύγκριση των εμβαδών;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 23 Ιουνίου, 2008 @ 7:57 μμ
Η διάμετρος ενός συνόλου είναι το μέγιστο (supremum για τους λεπτολόγους) των αποστάσεων ανάμεσα σε δύο σημεία του συνόλου. Άρα, αν τότε η διάμετρος του
τότε η διάμετρος του  είναι
είναι  της διαμέτρου του
της διαμέτρου του 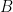 . Εφαρμόστε αυτό στα δύο κουτιά.
. Εφαρμόστε αυτό στα δύο κουτιά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Σεπτεμβρίου, 2009 @ 10:01 πμ
Νομιζω ειναι πλεον τετριμμενο. Η διαμετρος του μεγαλου ορθογωνιου παρ/δου ειναι ενω του μικρου ορθογωνιου παρ/δου
ενω του μικρου ορθογωνιου παρ/δου (εφαρμοσαμε δυο φορες Πυθαγορειο). Οποτε
(εφαρμοσαμε δυο φορες Πυθαγορειο). Οποτε 
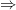
 . Προσθετοντας στην τελευταια σχεση δυο φορες την σχεση της 2ης υποδειξης
. Προσθετοντας στην τελευταια σχεση δυο φορες την σχεση της 2ης υποδειξης
ειναι
παιρνουμε το ζητουμενο στο τετραγωνο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από yannispantazis — 25 Σεπτεμβρίου, 2009 @ 5:08 μμ
Πολύ σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 25 Σεπτεμβρίου, 2009 @ 6:17 μμ