Το παρακάτω πρόβλημα είναι πλέον πολύ γνωστό αλλά, παρ’ όλ’ αυτά, πάντα έχει την ικανότητα να δημιουργεί συζητήσεις ατελείωτες και ενίοτε παθιασμένες.
Ο παίκτης Α παίζει με τον παίκτη Β το εξής παιχνίδι. Υπάρχουν τρεις κλειστές πόρτες και πίσω από μια από αυτές υπάρχει ένας θησαυρός. Πίσω από τις άλλες δεν υπάρχει τίποτα. Ο παίκτης Β γνωρίζει τι βρίσκεται πίσω από τις πόρτες και ο παίκτης Α όχι.
Κατ’ αρχήν ο παίκτης Α επιλέγει μια από τις πόρτες στην τύχη. Έπειτα, με βάση τους κανόνες του παιχνιδιού, ο παίκτης Β είναι υποχρεωμένος να ανοίξει στον Α μια άδεια πόρτα που είναι διαφορετική από αυτή που ο Α έδειξε (η οποία παραμένει κλειστή). Κατόπιν ο Β δίνει στον Α την ευκαιρία να επιλέξει αν θα επιμείνει στην αρχική του επιλογή ή θα επιλέξει την άλλη κλειστή πόρτα.
Εσείς τι θα κάνετε αν είσασταν στη θέση του παίκτη Α; Εννοείται εδώ ότι ο σκοπός του παίκτη Α είναι να παίξει με τέτοιο τρόπο ώστε να μεγιστοποιήσει την πιθανότητα να βρει το θησαυρό.
Γνωρίζω πιθανότητες, οπότε γνωρίζω και την «ανορθόδοξα» σωστή (από άποψη πιθανοτήτων) απάντηση.
Ο παίκτης Α έχει την μέγιστη πιθανότητα να βρει τον θησαυρό αν επιλέξει την άλλη κλειστή πόρτα.
Κι αυτό γιατί, αν υποθέσουμε (χωρίς πρόβλημα γενίκευσης) ότι ο θησαυρός είναι στην πόρτα Α, οι επιλογές του παίκτη Α είναι οι εξής (με Χ σημειώνω την πρώτη επιλογή του παίκτη):
Πόρτα Α Πόρτα Β Πόρτα Γ
1) Χ
2) Χ
3) Χ
Στην 1η περίπτωση, ο παίκτης Α θα επιλέξει την πόρτα Α. Ο παίκτης Β μπορεί να ανοίξει οποιαδήποτε από τις πόρτες Β και Γ. Ο παίκτης Α θα χάσει αν επιλέξει την άλλη κλειστή πόρτα και θα κερδίσει αν επιμείνει στην αρχική του επιλογή.
Στην 2η περίπτωση, ο παίκτης Α θα επιλέξει αρχικά την πόρτα Β. Τότε ο παίκτης Β θα του ανοίξει την πόρτα Γ. Ο παίκτης Α θα κερδίσει αν επιλέξει την άλλη κλειστή πόρτα και θα χάσει αν επιμείνει στην αρχική του επιλογή.
Στην 3η περίπτωση, ο παίκτης Α θα επιλέξει αρχικά την πόρτα Γ. Τότε ο παίκτης Β θα του ανοίξει την πόρτα Β. Ο παίκτης Α θα κερδίσει αν επιλέξει την άλλη κλειστή πόρτα και θα χάσει αν επιμείνει στην αρχική του επιλογή.
Οπότε, με πιθανότητα 2/3, ο παίκτης Α κερδίζει αν επιλέγει την άλλη κλειστή πόρτα και με πιθανότητα 1/3 κερδίζει αν επιμένει στην αρχική του επιλογή.
Στο ίδιο συμπέρασμα καταλήγουμε, αν ομοίως υποθέσουμε ότι ο θησαυρός βρίσκεται στις πόρτες Β ή Γ.
Άρα, η μεγιστοποίηση της πιθανότητας του παίκτη Α να βρει τον θησαυρό προκύπτει όταν επιλέγει κάθε φορά την άλλη κλειστή πόρτα…
🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από JChrist — 2 Απριλίου, 2008 @ 12:14 πμ
Ωραία.
Με άλλα λόγια, αν ο παίκτης Α παίξει με τη στρατηγική του «πάντα αλλάζω» τότε:
Στο τέλος παίρνει το θησαυρό αν και μόνο αν στην αρχική του επιλογή πόρτας έχει δείξει μια κενή πόρτα
πράγμα που συμβαίνει με πιθανότητα 2/3.
Σκεφθείτε τώρα και το εξής πρόβλημα:
Στα χέρια μου έχω ένα ποσό και το διπλάσιό του. Δεν ξέρετε ποιο είναι αυτό το ποσό. Επιλέγετε στην τύχη ένα από τα δύο μου χέρια, το ανοίγω και βλέπετε ένα ποσό, ας πούμε 1 ευρώ. Και σας δίνω τη δυνατότητα να πάρετε το 1 ευρώ ή να πάρετε αυτό που είναι στο άλλο χέρι (πριν σας το ανοίξω φυσικά).
Τι θα κάνετε;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Απριλίου, 2008 @ 12:56 μμ
Η προφανής διαφόρά από το προηγούμενο πρόβλημα είναι ότι εδώ οι δυνατές επιλογές είναι δύο. Έτσι ποτέ δεν μπορεί να επιλεγεί στρατηγική που κερδίει τα διπλάσια χρήματα με πιθανότητα πάνω από 1/2. Αυτό βέβαια με την προϋπόθεση ότι το χέρι που ανοίγει έχει 1 Ευρώ.
[[Τι θα γινόταν όμως αν το πρώτο χέρι που θα επιλέξω έχει 35 λεπτά; Τότε σίγουρα αλλάζοντας επιλογή κερδίζω τα διπλάσια!]]
Αξίζει όμως να γίνει και μια ακόμα ανάλυση. Εδώ το πρόβλημα παύει να είναι ποιοτικό, όπως πριν, και γίνεται ποσοτικό. Άρα δεν μας ενδιαφέρει το αν κερδίζουμε, αλλά και το πόσο κερδίζουμε. Έτσι η σωστή στρατηγική είναι πάντοτε να επιλέγουμε το άλλο χέρι. Αυτό γιατί πχ στο παράδειγμά μας το μέσο κέρδος που έχουμε είναι:
1/2*0,50+1/2*2=1,25 Ευρώ.
Σαν τζογαδόρος λοιπόν λέω ότι συμφέρει να το ρισκάρεις!
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 2 Απριλίου, 2008 @ 5:48 μμ
Με βάση τον νόμο του 50-50-90, δεν θα πάρει ποτέ το θησαυρό. Γιατί όταν οι πιθανότητες να βρεις κάτι είναι 50-50, είναι κατά 90% σίγουρο πως θα επιλέξεις το λάθος πράγμα. Ορίστε, και μαθηματικά διατυπωμένο, όπως ακριβώς το ήθελες!
Μου αρέσει!Μου αρέσει!
Σχόλιο από thogias — 2 Απριλίου, 2008 @ 9:48 μμ
nefelh:
Η ανάλυσή σου δεν εξαρτάται από το αν θα δεις 1 ευρώ ή άλλο ποσό. Ας πούμε ότι βλέπεις στο χέρι ένα ποσό . Τότε στο άλλο χέρι υπάρχει το ποσό
. Τότε στο άλλο χέρι υπάρχει το ποσό 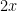 με πιθανότητα 1/2 και το ποσό
με πιθανότητα 1/2 και το ποσό  επίσης με πιθανότητα 1/2.
επίσης με πιθανότητα 1/2.
Άρα, αν παίζουμε πάντα το δεύτερο χέρι, η μέση τιμή του κέρδους μας θα είναι σε αντίθεση με το πρώτο χέρι που είναι, εξ ορισμού,
σε αντίθεση με το πρώτο χέρι που είναι, εξ ορισμού,  . Οπότε, όπως λες, συμφέρει να παίζουμε πάντα το δεύτερο χέρι.
. Οπότε, όπως λες, συμφέρει να παίζουμε πάντα το δεύτερο χέρι.
Σωστά;
Ή μήπως …;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Απριλίου, 2008 @ 11:48 μμ
Για την ιστορία, το αρχικό πρόβλημα είναι γνωστό ως «Monty Hall problem».
Θα συμφωνήσω με τους προλαλήσαντες, αν κάποιος κατασκευάσει το δέντρο αποφάσεων θα δει ότι το αναμενόμενο κέρδος είναι 1.25χ αν επιλέξει το κλειστό χέρι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από vildanden — 3 Απριλίου, 2008 @ 10:18 πμ
Μισό λεπτό όμως.
Έχω την εντύπωση ότι με το άνοιγμα του πρώτου χεριού ο παίκτης δεν παίρνει απολύτως καμία πληροφορία, αφού ότι και να δεί αυτός το ίδιο πράγμα θα πράξει (θα αλλάξει). Άρα πώς το που βλέπει γίνεται
που βλέπει γίνεται  (κατά μέσο όρο);
(κατά μέσο όρο);
Η ίδια αντίρρηση μπορεί να εκφραστεί και ως εξής. Ας πούμε ότι ο παίκτης ρίχνει νόμισμα κι αν έρθει κορώνα δείχνει το αριστερό χέρι αλλιώς το δεξί. Αν πρέπει να αλλάζει πάντα τότε καταλήγει να παίρνει τα περιεχόμενα του δεξιού χεριού αν έρθει κορώνα και του αριστερού αν έρθει γράμματα. Όμως αυτή η στρατηγική δεν είναι διαφορετική από το να μην αλλάζει ποτέ.
Τι γίνεται εδώ; Πρέπει να αλλάζουμε ή δεν κάνει διαφορά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Απριλίου, 2008 @ 12:22 πμ
Γειά χαρά σε όλους,
Αυτό που ξεχνάμε είναι ότι πάντα κερδίζουμε σε αυτό το παιχνίδι. Το θέμα είναι αν θα κεδίσουμε x/2, x ή 2x.
Προφανώς η πρώτη επιλογή γίνεται στη τύχη. Υπάρχουν δύο ισοπίθανα ενδεχόμενα α) να βρούμε το μεγάλο ποσό 2a και β) να βρούμε το μικρό ποσό a, στη πρώτη επιλογή.
Στην περίπτωση α) βλέπω to ποσό 2a και να είτε το κρατώ είτε αλλάζω χέρι και κερδίζω a.
Στη περίπτωση b) βλέπω a και είτε το κρατώ είτε αλλάζω χέρι και κερδίζω 2a.
Άρα, αν κρατήσω την αρχική επιλογή κερδίζω κατά μέσο όρο 1,5a και αν την αλλάξω κερδίζω πάλι 1,5a. Συνεπώς διαφορά δεν υπάρχει.
Η επιλογή αλλαγής χεριού δεν αλλάζει το μέσο κέρδος. Πρόκειται περισσότερο για μια δυνατότητα του παιχνιδιού που το κάνει πιο ενδιαφέρον καθώς προσφέρει μια ψευδαίσθηση επιλογής του αποτελέσματος, ώστε ο παίχτης τελικά να αισθάνεται τυχερός ή άτυχος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από filippop — 4 Απριλίου, 2008 @ 9:16 πμ
Λοιπόν, είναι νομίζω πλέον φανερό ότι δεν κάνει διαφορά το να αλλάζει κανείς χέρι ή όχι.
Τότε πού είναι το λάθος στο παρακάτω επιχείρημα;
Αν στο χέρι που δείξουμε την πρώτη φορά δούμε
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Απριλίου, 2008 @ 6:46 μμ
Νομίζω πως γενικά το σκεπτικό με τα ισοπίθανα ενδεχόμενα 2x και x/2 με μέση τιμή 1,25x έχει κάποιο λάθος.
Ας υποθέσουμε ότι στο ένα χέρι έχουμε x και στο άλλο y. Τότε, προφανώς y = 2x ή y = x/2 και η μέση τιμή του y είναι 1,25x. Ομοίως όμως x = y/2 ή χ = 2y x είναι 1,25y. (Άτοπο)
Αν τα ποσά που βρίσκονται στα δύο χέρια είναι a και 2a, τότε η μέση τιμή του x όσο και του y είναι 1,5a.
Άρα, στη πρώτη επιλογή το x είναι κατά μέσον όρο 1,5a (50% a και 50% 2α) και τα ποσά που θα κερδίσουμε αν αλλάξουμε χέρι είναι είτε a είτε 2a, με μέσο όρο 1,5a.
Η πληροφορία για το ποσό που υπάρχει στο ένα χέρι (πρώτη επιλογή) δεν είναι αρκετή για να μας δώσει να καταλάβουμε σε ποιο χέρι υπάρχει το μεγαλύτερο πόσο, ώστε να το επιλέξουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από filippop — 4 Απριλίου, 2008 @ 9:06 μμ
Διόρθωση
Ας υποθέσουμε ότι στο ένα χέρι έχουμε x και στο άλλο y. Τότε προφανώς, y = 2x ή y = x/2 και η μέση τιμή του y είναι 1,25x. Ομοίως όμως, x = y/2 ή x = 2y και μέση τιμή του x είναι 1,25y. (Άτοπο)
Μου αρέσει!Μου αρέσει!
Σχόλιο από filippop — 4 Απριλίου, 2008 @ 9:23 μμ
Τι είναι τυχαίο;
Αυτό σε γενικές γραμμές είναι το πρόβλημα του επιχειρήματος που έδωσα παραπάνω με το οποίο ισχυρίστηκα ότι είναι πιο συμφέρον να αλλάξει κανείς (πράγμα που είδαμε ότι δε μπορεί να ισχύει).
Κατ’ αρχήν πρέπει να ξεκαθαρίσουμε ότι τα ποσά που βρίσκονται στα χέρια, είτε θέλουμε να τα αποκαλέσουμε και
και 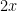 είτε
είτε  και
και  , δεν είναι τυχαία. Μας είναι άγνωστα αλλά όχι τυχαία. Τα ποσά που διάλεξε αυτός που υλοποιεί το παιχνίδι έχουν σταθεροποιηθεί αφότου τα διάλεξε. Το μόνο τυχαίο στο παιχνίδι είναι το ποιο χέρι από τα δύο διαλέγουμε.
, δεν είναι τυχαία. Μας είναι άγνωστα αλλά όχι τυχαία. Τα ποσά που διάλεξε αυτός που υλοποιεί το παιχνίδι έχουν σταθεροποιηθεί αφότου τα διάλεξε. Το μόνο τυχαίο στο παιχνίδι είναι το ποιο χέρι από τα δύο διαλέγουμε.
Γι’ αυτό είναι λάθος το να πούμε ότι το ποσό στο άλλο χέρι είναι με ίση πιθανότητα το διπλάσιο ή το μισό απ’ ό,τι έχουμε δει στο ανοιχτό χέρι ανεξάρτητα από το τι είναι αυτό που είδαμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Απριλίου, 2008 @ 2:45 μμ
Σωστά, παραμένει όμως το ερώτημα τελικά ποιά είναι αυτή η πιθανότητα;
Κλείδί στην επίλυση του παράδοξου είναι το ερώτημα ποιό είναι το εύρος τιμών που μπορεί να πάρει το x και με τι κατανομή πιθανοτήτων. Και πίσω από το παράδοξο κρύβεται, όπως σε πολλά παράδοξα, το άπειρο.
Αν το x μπορεί να πάρει πραγματικά οποιαδήποτε θετική τιμή, με ομοιόμορφη κατανομή πιθανοτήτων, και τελικά βγαίνει το 1, τότε ο χαρακτηρισμός της μεγαλύτερης γκαντεμιάς (ή τύχης) του σύμπαντος είναι λίγος! (Αν και διαισθητικά έχω την εντύπωση πως δεν μπορεί καν να φτιαχτεί μια θεωρητική μηχανή που παράγει τυχαίους αριθμούς από το σύνολο των ακέραιων θετικών με ομοιόμορφη κατανομή πιθανοτήτων. Αν γνωρίζει κάποιος κάτι παραπάνω επί του θέματος θα ήταν ενδιαφέρον.)
Σε κάθε περίπτωση, όταν μιλάμε για ένα πρακτικό πρόβλημα με ευρώ, το x μπορεί να πάρει τιμές από ένα συγκεκριμένο διάστημα, είτε αυτό είναι δεκάδες, είτε δισεκατομύρια!!! ευρώ. Οπότε, σε ένα πραγματικό πρόβλημα, πριν την επιλογή αν θα αλλάξουμε ή όχι χέρι, πρέπει να κάνουμε μια θεωρητική εκτίμηση της κατανομής πυκνότητας πιθανότητας του x με την οποία επέλεξε ο άλλος το x.
Αυτή η θεωρητική εκτίμηση μπορεί να γίνει λαμβάνοντας υπ’ όψη διάφορες παραμέτρους, όπως ποιός είναι ο άλλος, γιατί προσφέρει το ποσό, ποιό είναι το μέγιστο ποσό που μπορεί να προσφέρει (όπως είπαμε σε κάθε περίπτωση υπάρχει άνω όριο ακόμη και αν είναι ο μεγαλύτερος μεγιστάνας του κόσμου) κλπ.
Με βάση τα παραπάνω, μπορούν να γίνουν πολλές εκτιμήσεις και αναλύσεις. Παρακάτω θα περιγράψω δύο (πάντα θεωρητικές).
1. δεν ξέρω για ποιό λόγο ο άλλος προσφέρει κάποια λεφτά δωρεάν, αλλά καχύποπτα σκεφτόμενος θεωρώ ότι όσο μεγαλύτερο το ποσό, τόσο λιγότερες οι πιθανότητες. Μάλιστα, στην οριακή περίπτωση που η συνάρτηση κατανομής πυκνότητας πιθανότητας είναι της μορφής α/x (α σταθερά), η ΠΧΤ αν αλλάξουμε χέρι είναι ίδια με το ποσό που είχε το 1ο χέρι. Η σταθερά α εξαρτάται από το εύρος των τιμών που μπορεί να πάρει το x. Bέβαια, επειδή δεν ξέρουμε αν το αρχικό χέρι που επιλέξαμε είναι το x, το x/2 ή το 2x, υπάρχει ακόμη κάτι που μας ξεφεύγει, το οποίο θα το δούμε καλύτερα στο επόμενο παράδειγμα.
2. Υποθέτω (αυθαίρετα ή όχι) ότι η κατανομή πυκνότητας πιθανότητας του x είναι ομοιόμορφη με εύρος τιμών από 0 εώς 100000ευρώ. Τότε,
(α) αν στο πρώτο χέρι βρω πχ 8000ευρώ, τότε σύμφωνα με τα γνωστά αν επιλέξω το άλλο χέρι η ΠΧΤ είναι όντως 1.25*8000, οπότε πράγματι με συμφέρει να αλλάξω χέρι.
(β) αν στο 1ο χέρι βρω πχ 140000ευρώ, τότε είμαι σίγουρος ότι είμαι στην περίπτωση του 2x, οπότε το άλλο χέρι έχει 70000ευρώ και άρα δεν αλλάζω χέρι.
(γ) αν στο πρώτο χέρι βρω 80000ευρώ, τότε αυτό είτε είναι το x, είτε το 2x. (το x/2 δεν μπορεί να είναι, διότι τότε το x θα ήταν >100000). Με μια μικρή διερεύνηση των πιθανοτήτων (ενδιαφέρουσα άσκηση) μπορεί να δει κανείς αν συμφέρει να αλλάξει χέρι ή όχι.
ΔΙΕΥΚΡΙΝΗΣΗ1: θεωρώ ότι ο μηχανισμός επιλογής των ποσών στα δύο χέρια είναι: (α) επιλέγεται σύμφωνα με την κατανομή πιθανοτήτων ένας τυχαίος αριθμός x και τοποθετείται στο ένα χέρι
(β) επιλέγεται με τυχαίο τρόπο (πιθανότητες 50-50) είτε το x/2 είτε το 2x και τοποθετείται στο άλλο χέρι
ΔΙΕΥΚΡΙΝΗΣΗ2: θεωρώ ότι το κάθε χέρι δεν έχει πραγματικά λεφτά, αλλά επιταγές που μπορούν να περιέχουν τιμές με πολλά δεκαδικά. Αν έχει πραγματικά λεφτά, από χαρτονομίσματα των 500ευρώ μέχρι κέρματα του 1 λεπτού, τότε έχω μια ακόμη πληροφορία που μπορώ να χρησιμοποιήσω: αν το 1ο χέρι περιέχει ποσό με μονό αριθμό λεπτών, τότε είναι η περίπτωση x/2, οπότε αλλάζω χέρι δαγκωτό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από akonida — 29 Ιανουαρίου, 2010 @ 12:16 πμ