Στο πάτωμα βρίσκεται ένα σφαιρικό τόπι, που εφάπτεται στο σημείο Α του πατώματος. Παίρνετε αυτό το τόπι και παίζετε για λίγη ώρα. Αφού τελειώσετε το παιχνίδι αφήνετε ξανά το τόπι στο πάτωμα ώστε να ακουμπάει πάλι στο σημείο Α.
Ο προσανατολισμός του κατά τα άλλα μπορεί να είναι τυχαίος.
Δείξτε ότι υπάρχει κάποιο σημείο πάνω στο τόπι που βρίσκεται στις ίδιες 3-διάστατες συντεταγμένες που βρισκόταν και πριν πάρετε το τόπι για να παίξετε.
RSS feed for comments on this post. TrackBack URI
 | Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… |
 | Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; |
 | George Rizopulos στη Μπορείτε να σκοτώσετε τον… |
 | Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
 | ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Προβλήματα Μαθηματικών 
Αν καλά έχω εννοήσει το πρόβλημα.
Είναι το σημείο Κ της περιφέρειας της σφαίρας που ορίζει τη διάμετρο ΑΚ του νέου σημείου επαφής, με το κέντρο της σφαίρας. Αυτό το σημείο ευρίσκεται στις ίδιες 3-διάστατες συντεταγμένες, αφού δεν υπάρχει θέμα προσανατολισμού. Το Κ σταθερά και ανεξάρτητα από τον προσανατολισμό της σφαίρας, ήταν και εξακολουθεί να είναι το άλλο άκρο της ίδιας διαμέτρου.
Όλα τα σημεία της σφαίρας ευρίσκονται στις ίδιες 3-διάστατες συντεταγμένες και έχουν την ίδια ιδιότητα ζεύγους, αλλά επειδή δεν υπάρχει παρά μόνο ένα άκρο (αυτό που εκάστοτε ευρίσκεται το Α), δεν μπορούμε να τα προσδιορίσουμε. Επομένως όπως και να αφήσουμε το τόπι να εφάπτεται στο Α θα υπάρχει πάντα η ένδειξη του σημείου που δημιουργεί ή μάλλον υποδεικνύει το εξαρχής σταθερά υπαρκτό διαμετρικό ζεύγος με το σημείο στο Α.
Μου αρέσει!Μου αρέσει!
Σχόλιο από aplos — 1 Μαΐου, 2008 @ 11:21 πμ
Επεξήγηση:
Φανταστείτε ότι τα σημεία της επιφάνειας του τοπιού έχουν το καθένα το όνομά του, π.χ. γεωγραφικό πλάτος και γεωγραφικό μήκος ως πρός ένα σταθεροποιημένο «ισημερινό» (μέγιστο κύκλο) και μεσημβρινό (ένα σταθερό σημείο πάνω στον ισημερινό με, κατά σύμβαση, γεωγραφικό μήκος 0). Τα ονόματα των σημείων δεν αλλάζουν όσο διαρκεί το παιχνίδι.
Αυτό που ζητώ να δείξετε είναι ότι υπάρχει κάποιο σημείο του τοπιού (δηλ. ζεύγος γεωγραφικού πλάτους και μήκους) που θα επανέλθει στην ίδια θέση στο χώρο μετά το παιχνίδι, όπως και να ξανακουμπήσετε το τόπι στο σημείο Α του πατώματος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 1 Μαΐου, 2008 @ 7:16 μμ
Καταρχήν στο παιχνίδι με το τόπι οι μόνες κινήσεις που μπορούνε να γίνονται είναι φαντάζομαι μεταφορές και περιστροφές με άξονα στο κέντρο της μπάλας, διαδοχικά ή και ταυτόχρονα. Επειδή οι μεταφορές δεν παίζουνε ρόλο στην τελική θέση των σημείων, μπορούμε να υποθέσουμε εξαρχής ότι το τόπι υπόκειται μόνο σε ένα πλήθος περιστροφών. Από το γεγονός ότι οι περιστροφές αποτελούν ομάδα έπεται ότι μπορούμε να υποθέσουμε εν τέλει ότι το τόπι υπόκειται μόνο σε μία περιστροφή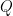
. Επειδή το χαρακτηριστικό πολυώνυμο της περιστροφής έκει βαθμό 3 και είναι πραγματικό, θα έχει τουλάχιστον μία πραγματική ρίζα και είτε άλλες δύο πραγματικές είτε δύο συζυγείς μιγαδικές. Όλες οι ρίζες, αφού είναι οι ιδιοτιμές της περιστροφής, έχουν απόλυτη τιμή 1. Είναι πολύ εύκολο τώρα να δει κανείς από τα παραπάνω ότι τουλάχιστον μία από τις ιδιοτιμές είναι το 1 (ο σταθερός όρος του πολυωνύμου είναι -1 και είναι – το γινόμενο των ριζών). Επομένως υπάρχει ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή 1, δηλαδή ένα σταθερό σημείο της περιστροφής.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ikonst — 4 Μαΐου, 2008 @ 1:56 μμ
ikonst:
Η κατεύθυνση που πήρες είναι η σωστή, αλλά γιατί είναι το 1 ιδιοτιμή; Δεν καταλαβαίνω το επιχείρημά σου. Μπορείς να το αναλύσεις λίγο παραπάνω;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Μαΐου, 2008 @ 5:26 μμ
Συγγνώμη, μα δεν έχω πολύ χρόνο για να επισκέπτομαι εδώ και γι’αυτό τα επιχειρήματά μου είναι πρόχειρα. Κοιτάξτε:
Επειδή η στροφή είναι ορθογώνιος μετασχηματισμός, κάθε ιδιοτιμή του έχει απόλυτη τιμή 1. Επιπλέον, η ορίζουσα του πίνακα είναι +1. Το χαρακτηριστικό πολυώνυμο έχει βαθμό 3 και είναι πραγματικό. Αυτό σημαίνει ότι θα έχει είτε μία ακριβώς πραγματική ρίζα και δύο συζυγείς μιγαδικές, είτε τρεις πραγματικές ρίζες(διότι αν ένα πραγματικό πολυώνυμο έχει μία μιγαδική ρίζα, έχει και τη συζυγή της).
Έστω ότι έχει τρεις πραγματικές ιδιοτιμές. Επειδή οι απόλυτες τιμές είναι 1 και το γινόμενο είναι 1, δε μπορεί και οι τρεις να είναι -1. Άρα τελειώσαμε σε αυτήν την περίπτωση.
Αν έχει δύο συζυγείς μιγαδικές και μία πραγματική, έχουμε ότι
διότι 
. Εδώ βέβαια r είναι η πραγματική ρίζα και c η μιγαδική και αντίστοιχα η συζυγής της.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ikonst — 5 Μαΐου, 2008 @ 12:42 μμ
Ο τύπος που δεν κάνει parse είναι
, ελπίζω να μην έχω άλλο τυπογραφικό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ikonst — 5 Μαΐου, 2008 @ 12:44 μμ
Τυπογραφικό όχι, αλλά γιατί είναι η ορίζουσα 1 και όχι -1;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Μαΐου, 2008 @ 1:01 μμ
Το rotation matrix διατηρεί τον προσανατολισμό του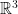
σε αντίθεση πχ. με το rotoinversion που αντιστρέφει τον προσανατολισμό. Αυτή η διατήρηση προσανατολισμού μεταφράζεται στο ότι η ορίζουσα είναι θετική.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ikonst — 5 Μαΐου, 2008 @ 1:19 μμ
Ουσιαστικά πρέπει να το εξάγεις από την υπόθεση: αν ο παίκτης που παίζει με το τόπι μπορεί να αλλάξει τον προσανατολισμό του χώρου ή της μπάλας ως προς το χώρο, σημαίνει ότι μπορεί να κάνει reflect τη μπάλα ως προς κάποιο επίπεδο. Θα ήθελα να δω έναν παίκτη να το κάνει αυτό: θα ζητωκραύγαζα κι ας μην ήταν καλός στο ποδόσφαιρο 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από ikonst — 5 Μαΐου, 2008 @ 1:24 μμ
Ωραία, αυτό ήταν που έλειπε, η διατήρηση του προσανατολισμού.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Μαΐου, 2008 @ 1:36 μμ
Κάπως όψιμα ίσως, αλλά το πρόβλημα αξίζει νομίζω την προσπάθεια για μια πιο εύληπτη απόδειξη😊:
Ας ονομάσουμε Χ και Ψ το αρχικό και το τελικό αντιστοίχως σημείο της μπάλας που ακουμπάει στο σημείο Α του δαπέδου. Έστω Ο το σταθερό κέντρο της μπάλας. Υπάρχουν δύο περιπτώσεις:
1. Τα σημεία Χ και Ψ ταυτίζονται: σε αυτή την περίπτωση, το σημείο Χ διατηρεί τις αρχικές του συντεταγμένες, που είναι οι συντεταγμένες του Α (το αντίστοιχο ισχύει και για το αντιδιαμετρικό ως προς το Χ σημείο της μπάλας).
2. Τα σημεία Χ και Ψ δεν ταυτίζονται: σε αυτή την περίπτωση, η αντικατάσταση τού Χ από το Ψ στη θέση επαφής της μπάλας με το σημείο Α του δαπέδου ισοδυναμεί με περιστροφή της μπάλας κατά γωνία ΨΟΧ (με φορά από την ΟΨ προς την ΟΧ) γύρω από άξονα κάθετο στο επίπεδο ΨΟΧ και διερχόμενο από το σημείο Ο. Τα δύο σημεία/πόλοι όπου ο άξονας αυτός τέμνει την επιφάνεια της μπάλας διατηρούν τις συντεταγμένες τους πριν και μετά από την περιστροφή.
Σε κάθε περίπτωση, το αποδεικτέο ισχύει για δύο τουλάχιστον σημεία της μπάλας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 3 Μαρτίου, 2018 @ 5:07 πμ