
Πάνω στο επίπεδο βρίσκεται ένας ψύλλος, ο οποίος είναι περιορισμένος να ζει και να κινείται πάνω στο σύνολο των ακεραίων σημείων του επιπέδου
. Τη χρονική στιγμή 0 βρίσκεται στο σημείο
και από κει και πέρα κινείται σε κάθε δευτερόλεπτο πηδώντας πάντα κατά το ίδιο διάνυσμα.
Με άλλα λόγια ο ψύλλος κινείται πάνω σε μια ευθεία και μάλιστα πάνω στα ακέραια σημεία της ευθείας αυτής, με σταθερή ταχύτητα. Για παράδειγμα θα μπορούσε σε κάθε ακέραια χρονική στιγμή να πηδάει κατά το διάνυσμα
.
Ο ψύλλος αυτός σας ενοχλεί και θέλετε να τον σκοτώσετε. Μπορείτε κάθε ακέραια χρονική στιγμή να χτυπάτε ένα από τα ακέραια σημεία του επιπέδου με την ελπίδα ότι ο ψύλλος βρίσκεται τότε εκεί και θα τον σκοτώσετε.
Δε βλέπετε όμως πού είναι ο ψύλλος (παρά μόνο αφού τον σκοτώσετε) ούτε ξέρετε ποιο είναι το διάνυσμα κίνησης του ψύλλου .
Μπορείτε να ακολουθήσετε μια μέθοδο χτυπημάτων που θα είναι σίγουρο ότι θα πετύχει τον ψύλλο αργά η γρήγορα; (Τη χρονική στιγμή 0 δε μπορείτε να χτυπήσετε. Αρχίζετε τη χρονική στιγμή 1.)
Έμαθα το πρόβλημα αυτό από τον Miklos Laczkovich.
Η λογική της απάντησης είναι να ελέγξουμε όλα τα πιθανά κοντινότερα σημεία που μπορει να βρίσκεται ο ψύλλος στην χρονική στιγμή t. Ώς β, ορίζω το μέγεθος βήματος του ψύλλου να είναι το απόλυτο μέγιστο μεταξύ των δύο συντεταγμένων για t=1. Δηλαδή βρίσκεται στο (x,y), με |y|>|x| για t=1, τοτε β=y. Ξεκινάμε…. Για t=1 τα κοντινότερα σημεία στο (0,0) στα οποία μπορεί να βρίσκεται ο ψύλλος είναι τα Ρ1,1 = {(1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1), (1,-1)} (αν ο ψύλλος έχει β=1). Σε αυτά τα σημεία είναι πιθανόν να βρίσκεται μόνο για t=1. Σε μετέπειτα χρονικές στιγμές αποκλείεται να βρίσκεται σε κάποια από αυτά. Ελέγχουμε την χρονική στιγμή t=1 μόνο ένα από τα P1, πχ το (1,0). Αν αποτύχουμε, τότε δεν έχει νόημα να έλεγξουμε κανένα άλλο του P1. Συνεχίζουμε όμως να θεωρούμε ότι μπορεί ο ψύλλος να έχει β=1. Τοτε για t=2, ο ψύλλος μπορεί να βρίσκεται στα P2,1={*(2,0)*, (2,2), (0,2), (-2,2), (-2,0), (-2,-2), (0, -2), (2,-2)}. To (2,0) [σε αστερίσκους], αποκλείεται να είναι την t=2, επειδή αν ήταν, θα το είχα ήδη βρει για t=1. Άρα ελέγχω μόνο το (2,2) [Αν το βρώ, τότε στην προηγούμενη χρονική στιγμή ήταν στο (1,1) που δεν ελεγξα]. Αν δεν το βρω, τότε για t=3, μπορεί να είναι στα P3,1={*(3,0)*, *(3,3)*, (0,3), …,(3,-3)}. Ελέγχω το (0,3), επειδή αποκλείεται να είναι στα (3,0), (3,3) [Αν ήταν θα τα είχα βρει στις προηγούμενες χρονικές στιγμές]. Συνεχίζω έτσι μέχρι και t=8, στο οποίο ελεγχω το (8, -8). Αν αποτύχω πάλι, τότε σίγουρα β!=1. Άρα το επόμενο που υποθέτω, είναι β=2. Βρίσκομαι στο t=9, και με β=2, τα σημεία που μπορεί να είναι το P1,2 = {(2*9=18,0), (18, 1*9=9), (18, 18), (9,18), (0,18), (-9,18), (-18, 18), (-18, 9), (-18,0), (-18, -9), (-18, -18), (-9, -18), (0, -18), (9, -18), (18, -18), (18, -9)}. Ελέγχω το πρώτο (18, 0). Αν δεν είναι τότε συνεχίζω να πιστέυω ότι το β=2, και για t=10 έχουμε τα πιθανά P2,2={*(20,0)*, (20, 9)…}. Ελεγχω το (20,9) [παρομοίως με προηγούμενα βήματα το (20,0) αποκλείεται γιατι αν ήταν θα το είχα ήδη βρει]. Νομίζω ότι μπορούμε να υπολογίσουμε και πόσος περίπου θα είναι ο αριθμός των ελεγχων που θα πρέπει να γίνουν δεδομενου του β του ψύλλου. Αν ο ψύλλος έχει βήμα β=κ, τότε θα χρειαστώ από Σ_{i=1}^{κ-1} 8i ως Σ_{i=1}^{κ} 8i βήματα ελέγχου. Εϊναι σωστή όλη αυτή η διαδικασία?
Μου αρέσει!Αρέσει σε 1 άτομο
Σχόλιο από Pavlos Pavlidis — 29 Αυγούστου, 2017 @ 9:45 πμ
Ναι γίνεται να τον πετύχουμε κάποια στιγμή, ουσιαστικα πρόκειται για ένα πρόβλημα αριθμησιμότητας.
Η ευθεία πάνω στην οποία κινείται ο ψύλλος εχει ρητή κλίση. Παίρνουμε μια αρίθμηση των ρητών (σε μια ορθογώνια διαταξη των ρητών περνάμε απειρες φορές πάνω από τον ίδιο ρητό). Συνεπώς μπορούμε να χτυπήσουμε άπειρα σημεία της ευθείας που κινείται ο ψύλλος(μπορούμε να θεωρήσουμε ημιευθείες
αντι για ευθείες).
Τώρα ο ψύλλος εχει κάποιο ‘»βήμα»,δηλαδή πηδάει ανά ένα τα σημεία της ευθείας ή ανα δυο ή ανα τρία και πάει λέγοντας.
Όποτε στην πρώτη ευθεία χτυπάμε το πρώτο της σημείο (άρα αν περναει απο αυτην με βήμα 1 τον χτυπάμε), στην δεύτερη χτυπάμε στο δεύτερο σημειο της (οποτε αν περνα απο αυτην με βήμα 1 τον χτυπάμε) και συνεχίζουμε.
Συνεπώς αν πηγαίνει με βήμα 1 θα τον πετύχουμε σε όποια ευθεία και αν κινείται.
Αλλιώς την δεύτερη φορά που θα περάσουμε από την πρώτη ευθεία θα χτυπήσουμε εκείνο το σημείο που θα είναι ο ψύλλος αν πηγαίνει με βήμα 2 (πχ αν περάσουμε ξανα μετά από n χτυπήματα από την πρώτη ευθεία θα χτυπήσουμε το 2n-οστό σημείο της ευθείας), αντίστοιχα για την δεύτερη ευθεία και όλες τις υπόλοιπες.
Συνεπώς αν πηγαίνει με βήμα 2 θα τον πετύχουμε σε όποια ευθεία και αν κινείται.
Συνεχίζουμε με αυτόν τον τρόπο, άρα όποιο βήμα και αν έχει ο ψύλλος σε όποια ευθεία και αν κινείται θα τον πετύχουμε κάποια στιγμή.
Το πρόβλημα μου το έδειξε η Ευή Παππαδάκη και προτείνουμε τη λύση μαζί.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Nikos Poursalidis — 29 Αυγούστου, 2017 @ 10:55 πμ
Σχόλιο 1: Ναι, σωστό είναι. Ας μου επιτραπεί να το εκφράσω λίγο πιο σύντομα.
Ας είναι το βήμα του ψύλλου, και ας γράψουμε
το βήμα του ψύλλου, και ας γράψουμε  για όλα τα πιθανά βήματα.
για όλα τα πιθανά βήματα.
Ο ψύλλος βρίσκεται στη θέση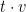 τη χρονική στιγμή
τη χρονική στιγμή 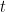 .
.
Οπότε αρκεί να χτυπήσουμε κατά σειρα στις θέσεις . Όποιο κι αν είναι το βήμα του ψύλλου θα χτυπηθεί κατ’ αυτόν τον τρόπο. Αν το βήμα είναι το
. Όποιο κι αν είναι το βήμα του ψύλλου θα χτυπηθεί κατ’ αυτόν τον τρόπο. Αν το βήμα είναι το 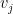 θα χτυπηθεί τη χρονική στιγμή
θα χτυπηθεί τη χρονική στιγμή 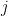 .
.
Την ώρα που γράφω αυτό δημοσιεύτηκε και το σχόλιο 2 παραπάνω που είναι κι αυτό σωστό.
Επιπλέον ερώτημα: Τι γίνεται αν οι ψύλλοι είναι τρεις και δεν ξέρουμε από πού ξεκίνησε ο καθένας από αυτούς;
Μου αρέσει!Αρέσει σε 1 άτομο
Σχόλιο από Mihalis Kolountzakis — 29 Αυγούστου, 2017 @ 10:59 πμ
Tha thewrhsw thn akolouthia sas

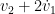
kai twra thewrw thn eksis akolouthia:
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexanagnostakis — 29 Αυγούστου, 2017 @ 11:41 μμ
Hello M Kolountzakis,
Estw oti exoume enan psyllo pou den kseroume apo pou ksekinaei:


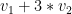

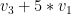

 kai kineitai me dieythynsh
kai kineitai me dieythynsh 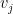 , tote meta apo n vhmata tha vrisketai sto
, tote meta apo n vhmata tha vrisketai sto 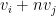
 .
.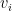 kai
kai 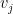 opote kseroume thn arxiki tou thesh kai pros ta pou kineitai molis ton vroume.
opote kseroume thn arxiki tou thesh kai pros ta pou kineitai molis ton vroume.
Tha thewrhsw thn akolouthia sas
kai twra thewrw thn eksis akolouthia:
Sthn ousia kathe fora pou exoume eksantlhsei tous syndyasmous prohgoumenwn dianysmatwn prosthetoume neo dianysma kai tous syndyasmous twn prohgoumenwn me ayto ksekinwntas me to prwto.
Estw oti o psyllos vrisketai arxika sto
Isxyrizomai oti o psyllos tha vrethei me ayth thn akolouthia se diakrito xrono
Etsi vriskoume ton psyllo kai malista mporoume na ksexwrisoume ta
Estw oti exoume 3:
Vriskoume ton 1o. Meta vgazontas apo th troxia tou 1ou psyllou vriskoume allon psyllo me thn idia methodo.
Ksana to idio gia ton 3o.
Ti lete?
Alex
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexanagnostakis — 30 Αυγούστου, 2017 @ 12:02 πμ
Mporoume omws pio genika na ftiaksoume thn akolouthia ws eksis pairnoume mia akolouthia wste
wste 
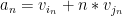 h opoia tha vrei th pseira otan
h opoia tha vrei th pseira otan 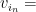 arxikh thesh
arxikh thesh  dianysma metatopishs.
dianysma metatopishs.
kai thewroume
Kai na stamathsoume molis vroume kai tis 3 pseires.
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexanagnostakis — 30 Αυγούστου, 2017 @ 1:35 πμ
Σχόλια 5 & 6: Πολύ σωστά.
Με άλλα λόγια, στην πορεία του ψύλλου αυτό που μας είναι άγνωστο είναι το ζεύγος (αρχική θέση, ταχύτητα). Οι δυνατές τιμές του ζεύγους αυτού είναι το σύνολο
(αρχική θέση, ταχύτητα). Οι δυνατές τιμές του ζεύγους αυτού είναι το σύνολο  , ένα αριθμήσιμο σύνολο. Παίρνουμε λοιπόν ένα-ένα όλα τα στοιχεία του συνόλου αυτού και κάθε φορά κοιτάμε πού θα ήταν ο ψύλλος αν αυτές ήταν οι παράμετροί του και χτυπάμε εκεί. Με τον τρόπο αυτό κάποτε θα τον πετύχουμε.
, ένα αριθμήσιμο σύνολο. Παίρνουμε λοιπόν ένα-ένα όλα τα στοιχεία του συνόλου αυτού και κάθε φορά κοιτάμε πού θα ήταν ο ψύλλος αν αυτές ήταν οι παράμετροί του και χτυπάμε εκεί. Με τον τρόπο αυτό κάποτε θα τον πετύχουμε.
Επιπλέον ερώτημα: Ο ψύλλος τώρα είναι πολύ πιο έξυπνος. Δεν κινείται δηλ. αναγκαστικά πάνω σε μια ευθεία. Αυτό που ισχύει είναι ότι πρόκειται για ένα ψύλλο robot ο οποίος είναι προγραμματισμένος να εκτελεί μια κίνηση στο επίπεδο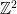 . Θα μπορούσε π.χ. να είναι προγραμματισμένος στις άρτιες χρονικές στιγμές να μένει ακίνητος και τις περιττές χρονικές στιγμές να κινείται κατά το διάνυσμα
. Θα μπορούσε π.χ. να είναι προγραμματισμένος στις άρτιες χρονικές στιγμές να μένει ακίνητος και τις περιττές χρονικές στιγμές να κινείται κατά το διάνυσμα  . Ή, να κάνει κάτι πολύ πιο πολύπλοκο, όπως, π.χ., να αποφέυγει τελείως το αριστερό ημιεπίπεδο κι όποτε μπαίνει εκεί μέσα να γυρνάει αμέσως προς τα δεξιά και να φεύγει.
. Ή, να κάνει κάτι πολύ πιο πολύπλοκο, όπως, π.χ., να αποφέυγει τελείως το αριστερό ημιεπίπεδο κι όποτε μπαίνει εκεί μέσα να γυρνάει αμέσως προς τα δεξιά και να φεύγει.
Δεν ξέρουμε το πρόγραμμα με το οποίο είναι εφοδιασμένος ο ψύλλος, ούτε, και πάλι, από το πού ξεκίνησε.
Πώς μπορούμε να τον σκοτώσουμε;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 30 Αυγούστου, 2017 @ 8:12 πμ
Για το τελευταίο Επιπλέον ερώτημα: Ένας ψύλλος που μπορεί να κάνει τέτοια ωραία πράγματα, όπως να αποφεύγει το αριστερό ημιεπίπεδο (αν απέφευγε το δεξί, θα ήταν διάνοια, δεν το συζητώ!) δεν αξίζει το θάνατο, αλλά την αγάπη και τη φροντίδα μας! Ούτε ψύλλος στον κόρφο μας αν τον σκοτώσουμε… 🙂
Ωραία η επαναμφάνισή σου Μιχάλη, κι ωραίο πρόβλημα!
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 30 Αυγούστου, 2017 @ 8:42 πμ
Μπορεί να μη θέλουμε να τον σκοτώσουμε αλλά να τον βρούμε και να του δώσουμε ένα φιλάκι. Ίδιο πρόβλημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 30 Αυγούστου, 2017 @ 9:35 πμ
Στην περίπτωση του ψύλλου ρομπότ, μια σκέψη θα ήταν η εξής: Εδώ έχουμε άγνωστο το ζευγάρι (α,π) δηλαδή την αρχική θέση και το πρόγραμμα κίνησης που το φανταζόμαστε σαν μια συνάρτηση που επιστρέφει τη θέση του ψύλλου σε κάθε στιγμή t=1,2,3,… όταν η θέση του τη στιγμή t=0 είναι α. Αλλά το σύνολο των δυνατών προγραμμάτων, ως πεπερασμένων ακολουθιών πεπερασμένου πλήθους συμβόλων, είναι αριθμήσιμο. Αριθμώντας επομένως με κάποιον τρόπο (π.χ. λεξικογραφικά) τα προγράμματα (π=1,2,3,…), όπως και τις αρχικές θέσεις, αναγόμαστε στις προηγούμενες περιπτώσεις, άρα με βεβαιότητα κάποτε θα πετύχουμε τον ψύλλο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 1 Σεπτεμβρίου, 2017 @ 8:06 μμ
10: Σωστή προσέγγιση και σχεδόν δουλεύει, αλλά υπάρχει ένα πρόβλημα. Ποιο να είναι αυτό;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 1 Σεπτεμβρίου, 2017 @ 8:15 μμ
Η απειρία των προγραμμάτων; Και ότι θα πρέπει να τα γράψουμε όλα για να μπορέσουμε να τα αριθμήσουμε, με οποιοδήποτε τρόπο;
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 1 Σεπτεμβρίου, 2017 @ 8:28 μμ
12: Το ότι τα προγράμματα είναι άπειρα στο πλήθος δεν είναι πρόβλημα (και τα διανύσματα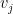 πιο πάνω πάλι άπειρα είναι, αλλά το σημαντικό και στις δύο περιπτώσεις είναι ότι είναι αριθμήσιμα). Επίσης δε χρειάζεται να τα γράψεις όλα για να τα αριθμήσεις. Αρχίζεις και παράγεις όλες τις λέξεις (από το αλφάβητο του υπολογιστή σου) μήκους 1, 2, 3, κλπ, οι οποίες για κάθε μήκος είναι πεπερασμένες στο πλήθος, και για κάθε μια από αυτές ελέγχεις αλγοριθμικά το αν είναι σωστό συντακτικά πρόγραμμα (compiler λέγεται ένα τέτοιο πρόγραμμα ή interpreter και υπάρχουν πολλά τέτοια προγράμματα) και αν δεν είναι το πετάς αλλιώς το βάζεις στην αρίθμησή σου.
πιο πάνω πάλι άπειρα είναι, αλλά το σημαντικό και στις δύο περιπτώσεις είναι ότι είναι αριθμήσιμα). Επίσης δε χρειάζεται να τα γράψεις όλα για να τα αριθμήσεις. Αρχίζεις και παράγεις όλες τις λέξεις (από το αλφάβητο του υπολογιστή σου) μήκους 1, 2, 3, κλπ, οι οποίες για κάθε μήκος είναι πεπερασμένες στο πλήθος, και για κάθε μια από αυτές ελέγχεις αλγοριθμικά το αν είναι σωστό συντακτικά πρόγραμμα (compiler λέγεται ένα τέτοιο πρόγραμμα ή interpreter και υπάρχουν πολλά τέτοια προγράμματα) και αν δεν είναι το πετάς αλλιώς το βάζεις στην αρίθμησή σου.
Αλλού είναι το πρόβλημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Σεπτεμβρίου, 2017 @ 8:30 πμ
Για να κάνω τα πράγματα λίγο πιο συγκεκριμένα, ας πούμε ότι ο ψύλλος έχει ένα πρόγραμμα που του λέει σε ποια θέση να πάει τη χρονική στιγμή
που του λέει σε ποια θέση να πάει τη χρονική στιγμή 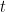 . Μπορούμε να σκεφτόμαστε το πρόγραμμα
. Μπορούμε να σκεφτόμαστε το πρόγραμμα 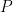 ως μια υπολογίσιμη συνάρτηση
ως μια υπολογίσιμη συνάρτηση  , και ως υπολογίσιμη συνάρτηση δίνεται από κάποιο πρόγραμμα το οποίο δεν είναι τίποτε άλλο από μια, ενδεχομένως μεγάλη, αλλά πεπερασμένη λέξη στην αγαπημένη σας γλώσσα προγραμματισμού. Όπως περιγράφω στο σχόλιο 13 παραπάνω μπορεί κανείς να φτιάξει ένα πρόγραμμα που να παράγει το ένα μετά το άλλο όλα τα προγράμματα
, και ως υπολογίσιμη συνάρτηση δίνεται από κάποιο πρόγραμμα το οποίο δεν είναι τίποτε άλλο από μια, ενδεχομένως μεγάλη, αλλά πεπερασμένη λέξη στην αγαπημένη σας γλώσσα προγραμματισμού. Όπως περιγράφω στο σχόλιο 13 παραπάνω μπορεί κανείς να φτιάξει ένα πρόγραμμα που να παράγει το ένα μετά το άλλο όλα τα προγράμματα 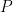 , που είναι φυσικά αριθμήσιμα στο πλήθος. Ας πούμε λοιπόν ότι
, που είναι φυσικά αριθμήσιμα στο πλήθος. Ας πούμε λοιπόν ότι  είναι το j-οστό πρόγραμμα που παράγεται. Γιατί να μη χτυπάμε στη θέση
είναι το j-οστό πρόγραμμα που παράγεται. Γιατί να μη χτυπάμε στη θέση 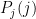 ; Δε θα χτυπήσουμε έτσι τον ψύλλο, όποιο και να είναι το πρόγραμμα που τον διέπει;
; Δε θα χτυπήσουμε έτσι τον ψύλλο, όποιο και να είναι το πρόγραμμα που τον διέπει;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 2 Σεπτεμβρίου, 2017 @ 9:21 πμ
Σαφές και κομψό, αλλά δεν αντιλαμβάνομαι σε τι διαφέρει από την προσέγγιση του σχολίου 10. Πού ήταν (ή είναι) τελικά το πρόβλημά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 3 Σεπτεμβρίου, 2017 @ 2:02 μμ
Φανταστείτε ότι ακολουθείτε λοιπόν τη στρατηγική που περιγράφω στο σχόλιο 14, ότι κάποιος το λέει στον ψύλλο κι αυτός αποφασίζει τη χρονική στιγμή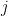 να πηδάει στη θέση
να πηδάει στη θέση 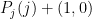 (εφόσον εσείς ακολουθείτε ένα αλγοριθμικό τρόπο να κινείστε, άρα το ίδιο κάνει κι ο ψύλλος με αυτή τη στρατηγική που ακολουθεί). Έτσι όμως δε θα τον πετύχετε ποτέ.
(εφόσον εσείς ακολουθείτε ένα αλγοριθμικό τρόπο να κινείστε, άρα το ίδιο κάνει κι ο ψύλλος με αυτή τη στρατηγική που ακολουθεί). Έτσι όμως δε θα τον πετύχετε ποτέ.
Δεν πάει κάτι στραβά λοιπόν με το επιχείρημα;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 3 Σεπτεμβρίου, 2017 @ 8:36 μμ
Erwthsh:
Ta programmata mhpws einai mh arithmisima omws?
emena mou fainetai oti einai
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexanagnostakis — 5 Σεπτεμβρίου, 2017 @ 1:32 μμ
17: Όχι. Τα προγράμματα είναι αριθμήσιμα στο πλήθος. Κάθε πρόγραμμα είναι μια πεπερασμένη λέξη από ένα πεπερασμένο αλφάβητο (με, π.χ., καμια 100στή σύμβολα), άρα είναι αριθμήσιμα στο πλήθος.
Αλλού είναι το πρόβλημα, και είναι πολύ πιο ενδιαφέρον από την πληθικότητα των προγραμμάτων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Σεπτεμβρίου, 2017 @ 1:39 μμ
Λίγο ακόμη ξεκαθάρισμα της κατάστασης.
Υπάρχουν δύο διαφορετικές περιπτώσεις όσον αφορά τις δυνατότητες τις δικές σας.
1. Είστε υπεράνθρωπος, έχετε άπειρη μνήμη και με κάποιον τρόπο έχετε εξασφαλίσει την ακολουθία όλων των δυνατών προγραμμάτων που μπορεί να ακολουθεί ο ψύλλος. Τότε η μέθοδος που περιγράφεται στο σχόλιο 14 δουλεύει μια χαρά. Η αντίφαση που περιγράφεται στο σχόλιο 16 δεν υφίσταται γιατί δεν υπάρχει αλγοριθμικός τρόπος για τον ψύλλο (ο οποίος πάντα υποτίθεται ότι είναι robot, άρα πάντα εκτελεί κάποιο πρόγραμμα) να πάει στη θέση
όλων των δυνατών προγραμμάτων που μπορεί να ακολουθεί ο ψύλλος. Τότε η μέθοδος που περιγράφεται στο σχόλιο 14 δουλεύει μια χαρά. Η αντίφαση που περιγράφεται στο σχόλιο 16 δεν υφίσταται γιατί δεν υπάρχει αλγοριθμικός τρόπος για τον ψύλλο (ο οποίος πάντα υποτίθεται ότι είναι robot, άρα πάντα εκτελεί κάποιο πρόγραμμα) να πάει στη θέση 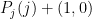 , γιατί πολύ απλά δεν έχει αλγοριθμικό τρόπο να παράγει το
, γιατί πολύ απλά δεν έχει αλγοριθμικό τρόπο να παράγει το  πρόγραμμα. Με αυτή την υπόθεση το πρόβλημα έχει τελειώσει.
πρόγραμμα. Με αυτή την υπόθεση το πρόβλημα έχει τελειώσει.
2. Είστε κι εσείς robot. Και απλός άνθρωπος να είστε πάλι, αν είναι να κάνετε κάτι για άπειρα βήματα ουσιαστικά ο μόνος τρόπος να το κάνετε είναι να τρέχετε ένα πρόγραμμα. Σε αυτή την περίπτωση η αντίφαση του σχολίου 16 υπάρχει και αυτό που απομένει είναι να την ξεκαθαρίσουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 8 Σεπτεμβρίου, 2017 @ 10:00 πμ
Ας προσπαθήσω να κινήσω ξανά το ενδιαφέρον σας. Υπάρχουν πολύ σοβαρά συμπεράσματα που μπορούν να βγουν από αυτό το αδιέξοδο στο οποίο έχουμε έρθει.
Αναφερόμενος στο Σχόλιο 19, περίπτωση 2, είναι φανερό ότι το να κάνει ο άνθρωπος robot τη διαδικασία που περιγράφεται παραπάνω στο Σχόλιο 14 είναι αδύνατο, ακριβώς γιατί οδηγεί σε αντίφαση. Άρα, κάτι από αυτά που πρέπει να κάνει κανείς στο Σχόλιο 14 είναι αδύνατο.
Το να παράγει κανείς αλγοριθμικά (με ένα πρόγραμμα δηλ.) όλα τα συντακτικά σωστά προγράμματα που υπάρχουν, το ένα μετά το άλλο, όχι μόνο είναι δυνατό να γίνει αλλά είναι και εύκολο. Φτιάχνουμε ένα πρόγραμμα που παράγει το ένα μετά το άλλο όλα τα πεπερασμένα κείμενα και για κάθε κείμενο που παράγεται το ελέγχουμε αν είναι συντακτικά σωστό. Κάτι που γίνεται φυσικά, φαναταστείτε όταν γράφετε στον υπολογιστή σας ένα πρόγραμμα σε μια γλώσσα προγραμματισμού και όταν πάτε να το τρέξετε ο υπολογιστής το πρώτο που κάνει είναι να το ελέγξει συντακτικά. Αν δεν είναι ΟΚ σας το λέει για να το διορθώσετε. Άρα η αλγοριθμική απαρίθμηση όλων των πιθανών προγραμματων είναι εφικτή.
Όταν όμως έρθει η ώρα να υπολογίσετε τη θέση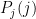 για να μεταβείτε εκεί τη χρονική στιγμή
για να μεταβείτε εκεί τη χρονική στιγμή 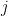 τότε πώς το κάνετε αυτό; Βάζετε φυσικά το πρόγραμμα
τότε πώς το κάνετε αυτό; Βάζετε φυσικά το πρόγραμμα  , το οποίο μόλις έχετε βρει, να τρέξει με είσοδο
, το οποίο μόλις έχετε βρει, να τρέξει με είσοδο 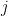 .
.
Κι αν αυτό το πρόγραμμα δεν τελειώσει ποτέ;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Σεπτεμβρίου, 2017 @ 8:44 πμ
Αν το αντιλαμβάνομαι σωστά, για να βγούμε και από αυτό το αδιέξοδο θα χρειαζόμασταν ακόμα ένα πρόγραμμα που να μας λέει αν ο εκάστοτε συνδυασμός προγράμματος – εισόδου τερματίζει ή όχι, έτσι ώστε να εξαιρέσουμε από την αρίθμησή μας τα προγράμματα που δεν τερματίζουν. Ο Turing από ό,τι θυμάμαι είχε αποδείξει ότι ένα τέτοιο πρόγραμμα δεν μπορεί να υπάρχει. Δεν είμαι σίγουρος όμως πως ο αγαπητός Μιχάλης δεν έχει και σε αυτό κάποια απάντηση! 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 29 Σεπτεμβρίου, 2017 @ 1:46 μμ
21: Απολύτως σωστά.
Για να μπορούμε να ακολουθήσουμε τον αλγόριθμο εξολόθρευσης του ψύλλου που περιγράφεται στο σχόλιο 14 είναι απαραίτητο εκτός από το να μπορούμε (αλγοριθμικά) να ξεχωρίσουμε πότε ένα κείμενο είναι ένα συντακτικά σωστό πρόγραμμα, πρέπει να μπορούμε και εκτός των άλλων να αποφασίζουμε (αλγοριθμικά) το πότε ένα πρόγραμμα σταματάει. Αυτό είναι αδύνατο. Δε χρειάζεται να στηριχθούμε σε κάποιο θεώρημα για αυτό. Το αποδείξαμε εμείς εδώ. Πώς; Μα αν υπήρχε τέτοιο πρόγραμμα τότε ο αλγόριθμος εξολόθρευσης του σχολίου 14 θα δούλευε και θα σκότωνε τον ψύλλο. Όμως και ο αλγόριθμος αποφυγής του ψύλλου (στο σχόλιο 16) θα δούλευε κι έτσι δε θα τον χτυπάγαμε ποτέ, αντίφαση. Άρα αλγόριθμος που αποφασίζει πότε ένα πρόγραμμα τερματίζει δεν υπάρχει. Αγγλιστί, the halting problem is undecidable. Όχι ότι οι αποδείξεις που μπορεί κανείς να βρει στα βιβλία είναι πιο δύσκολες. Αλλά ο ψύλλος έχει πιο πλάκα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Σεπτεμβρίου, 2017 @ 7:32 μμ
Να βάλω ένα επιπλέον ερώτημα;
Πώς σκοτώνουμε τον ψύλλο αν ζει και κινείται στο Q^2 , δηλαδή κινείται σε rational coordinates, και δεν ξέρουμε την αρχική του θέση;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Μαρτίου, 2022 @ 12:04 πμ
23: Νομίζω ότι δεν αλλάζει κάτι από την περίπτωση που ο ψύλλος κινείται στο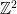 . Δε χρησιμοποιούμε κάπου τη δομή ή γεωμετρία του διακριτού επιπέδου αλλά μόνο το ότι είναι ένα αριθμήσιμο σύνολο και μπορούμε αλγοριθμικά να απαριθμήσουμε τα στοιχεία του, πράγμα που ισχύει και για το
. Δε χρησιμοποιούμε κάπου τη δομή ή γεωμετρία του διακριτού επιπέδου αλλά μόνο το ότι είναι ένα αριθμήσιμο σύνολο και μπορούμε αλγοριθμικά να απαριθμήσουμε τα στοιχεία του, πράγμα που ισχύει και για το 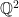 .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Μαρτίου, 2022 @ 11:53 μμ
Ναι , βέβαια Μιχάλη! Το σκέφτηκα λίγο μετά που το πόσταρα, αλλά είπα να το αφήσω, just in case…
Θα μπορούσε ας πούμε η «σπείρα» των χτυπημάτων μας (διανυσματων) να ακολουθήσει την κλασική enumeration των ρητών αριθμών απ το «διαγώνιο επιχείρημα» του Κάντορ: 1/1 —>1/2—> 1/3–>2/2–>3/1–>4/1–>3/2–> etc
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 29 Μαρτίου, 2022 @ 3:10 μμ