Γνωρίζουμε πολύ καλά ότι αν είναι τα συνηθισμένα διανύσματα βάσης στο επίιπεδο
τότε κάθε διάνυσμα
μπορεί να γραφεί ως:
.
Μπορεί δηλ. να γραφεί το ως γραμμικός συνδυασμός των
όπου οι συντελεστές είναι απλά τα εσωτερικά γινόμενα με τα διανύσματα αυτά. Το ίδιο φυσικά ισχύει αν στη θέση των
βάλουμε δύο οποιαδήποτε ορθογώνια μεταξύ τους διανύσματα του επιπέδου με μέτρο 1.
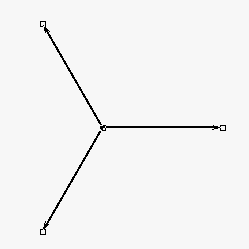
Αν και
είναι οι περιστροφές του
κατά
αντίστοιχα (όπως φαίνονται στο σχήμα παραπάνω), δείξτε ότι και για τα
ισχύει ότι κάθε διάνυσμα
μπορεί να γραφεί ως:
.
εχουμε το φ1=(6^(1/2)/3, 0) αρα απο τον πινακα στροφης για 2π/3 και -2π/3 αντιχτοιχα βρισκουμε:
φ2=(-6^(1/2)/6, 2^(1/2)/2) και
φ3=(-6^(1/2)/6, -2^(1/2)/2).
μετα αν u=(x,y) και υπολογισουμε τα εσωτερικα γινομενα:
=6^(1/2)/3*x
=-6^(1/2)/6*x+ 2^(1/2)/2*y
=-6^(1/2)/6*x- 2^(1/2)/2*y
μετα εχουμε:
φ1=(2/3*x, 0)
φ2=(1/6*x-3^(1/2)/6*y, -3^(1/2)/6*x+1/2*y)
φ3=(1/6*x+3^(1/2)/6*y, 3^(1/2)/6*x+1/2*y)
και υπολογιζουμε το αθροισμα τους που ειναι ισο με (x, y) αρα ισο με το u..
δεν ξερω αν εννοειτε να το αποδειξουμε αλλιως, χωρις πραξεις δηλαδη…
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 4 Ιουλίου, 2015 @ 5:18 μμ
δεν εμφανισε τα εσωτερικα γινομενα… το αντιγραφω απο εκεινο το σημειο:
μετα αν u=(x,y) και υπολογισουμε τα εσωτερικα γινομενα:
(u,φ1)=6^(1/2)/3*x
(u,φ2)=-6^(1/2)/6*x+ 2^(1/2)/2*y
(u,φ3)=-6^(1/2)/6*x- 2^(1/2)/2*y
μετα εχουμε:
(u,φ1)φ1=(2/3*x, 0)
(u,φ2)φ2=(1/6*x-3^(1/2)/6*y, -3^(1/2)/6*x+1/2*y)
(u,φ3)φ3=(1/6*x+3^(1/2)/6*y, 3^(1/2)/6*x+1/2*y)
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 4 Ιουλίου, 2015 @ 5:23 μμ
1, 2: Πολύ σωστά.
Βέβαια, μια απόδειξη με πράξεις, παρά το ότι είναι σωστή, μερικές φορές (όπως αυτή) δε μας επιτρέπει να κατανοήσουμε κάτι τόσο καλά. Η περίπτωση που ζητώ παραπάνω είναι απλά μια ειδική περίπτωση.
Αποδείξτε λοιπόν ότι αν αν είναι οι κορυφές ενός κανονικού πολυγώνου, εγγεγραμμένου στο μοναδιαίο κύκλο, τότε υπάρχει μια σταθερά
είναι οι κορυφές ενός κανονικού πολυγώνου, εγγεγραμμένου στο μοναδιαίο κύκλο, τότε υπάρχει μια σταθερά 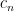 (βρείτε την) τέτοια ώστε, αν
(βρείτε την) τέτοια ώστε, αν 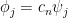 ,
, 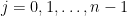 , τότε ισχύει και πάλι, για κάθε διάνυσμα
, τότε ισχύει και πάλι, για κάθε διάνυσμα 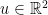 :
:
Δείξτε επίσης ότι , όπου
, όπου  είναι το Ευκλείδιο μέτρο (το συνηθισμένο μας μήκος) του διανύσματος
είναι το Ευκλείδιο μέτρο (το συνηθισμένο μας μήκος) του διανύσματος  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Ιουλίου, 2015 @ 8:44 μμ
η σχεση που πρεπει να ισχυει ειναι η:
u=|u||φ0|cosθ0*φ0+|u||φ1|cosθ1*φ1+….+|u||φn-1|cosθn-1*φn-1 ,οπου θj ειναι η γωνια μεταξυ u και φj,
ομως εχουμε φj=Cn*ψj και αρα |φj|=|Cn|*|ψj| οπου |ψj|=1 για καθε j αφου ειναι στο μοναδιαιο κυκλο. Αρα |φj|=|Cn| για καθε j.
Ετσι η σχεση γινεται:
u=|u||Cn|cosθ0*(Cn*ψ0)+|u||Cn|cosθ1*(Cn*ψ1)+….+|u||Cn|cosθn-1*(Cn*ψn-1)
και βαζοντας μετρα και στα δυο μελη εχουμε:
|u|=|u||Cn|^2*(|cosθ0*ψ0+cosθ1*ψ1+….+cosθn-1*ψn-1|)
αρα:
1=|Cn|^2*(|cosθ0*ψ0+cosθ1*ψ1+….+cosθn-1*ψn-1|) αρα
Cn=+-1/(|cosθ0*ψ0+cosθ1*ψ1+….+cosθn-1*ψn-1|)^(1/2)
το βρηκα συναρτησει των θ και ψ.. σωστο ειναι??
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 6 Ιουλίου, 2015 @ 12:26 πμ
4: Οι υπολογισμοί σου είναι σωστοί αλλά το μόνο που δείχνουν είναι το ποια πρέπει να είναι η τιμή του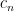 αν γνωρίζεις το διάνυσμα
αν γνωρίζεις το διάνυσμα  . Όμως για να αποδείξεις τον ισχυρισμό πρέπει να αποδείξεις ότι το
. Όμως για να αποδείξεις τον ισχυρισμό πρέπει να αποδείξεις ότι το 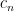 είναι μια σταθερά, εξαρτάται δηλ. από το
είναι μια σταθερά, εξαρτάται δηλ. από το  και μόνο, και όχι από το
και μόνο, και όχι από το  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Ιουλίου, 2015 @ 7:40 πμ
ενταξει θα προσπαθησω αλλιως… Αν u=(x,y) διανυσμα γραμμη (1×2) και εστω Α ο πινακας με στηλες τα φj (2xn) δηλαδη
Α=(φ1x, φ2x, …, φnx
φ1y, φ2y, …, φny)
τοτε u*A=(u*φ1, u*φ2, …., u*φn) δηλαδη (1xn) διανυσμα γραμμη με τα εσωτερικα γινομενα u*φj
και αν Β ειναι ο αναστροφος του Α (nx2) τοτε παρατηρουμε οτι u*Α*Β (γραμμη (1×2)) ειναι το αθροισμα που θελουμε και για να ισουται με u πρεπει Α*Β=I οπου I ειναι ο ταυτοτικος 2×2 πινακας… ομως
Α*Β= [Cn^2*(ψ1x^2+ψ2x^2+….+ψnx^2), Cn^2(ψ1x*ψ1y+ψ2x*ψ2y+….+ψnx*ψny)
Cn^2(ψ1x*ψ1y+ψ2x*ψ2y+….+ψnx*ψny), Cn^2*(ψ1y^2+ψ2y^2+….+ψny^2)]
αρα πρεπει:
Cn^2*(ψ1x^2+ψ2x^2+….+ψnx^2)= Cn^2*(ψ1y^2+ψ2y^2+….+ψny^2)= 1
ομως αφου ψjx^2+ψjy^2=1 εχουμε απο την πρωτη ισοτητα οτι:
Cn^2*(ψ1x^2+ψ2x^2+….+ψnx^2)=Cn^2*(n-(ψ1x^2+ψ2x^2+….+ψnx^2)) αρα
ψ1x^2+ψ2x^2+….+ψnx^2= n/2
και απο την αλλη ισοτητα (Cn^2*(ψ1x^2+ψ2x^2+….+ψnx^2)=1) εχουμε:
Cn^2*(n/2)=1 αρα Cn=(2/n)^(1/2)
Επισης πρεπει: Cn^2(ψ1x*ψ1y+ψ2x*ψ2y+….+ψnx*ψny)=0 δηλαδη
ψ1x*ψ1y+ψ2x*ψ2y+….+ψnx*ψny=0 που ισχυει αλλα δεν ξερω γιατι… :p
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 6 Ιουλίου, 2015 @ 6:30 μμ
Μέχρι το σημείο που γράφεις ότι πρέπει να δείξεις ότι ο πίνακας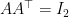 όλα καλά κι ωραία.
όλα καλά κι ωραία.
Αλλά από κει και κάτω παρατήρησε ότι δε χρησιμοποιείς πουθενά την πλήρη υπόθεσή σου παρά μόνο το ότι τα διανύσματα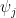 είναι μοναδιαία. Άρα κάπου υπάρχει λάθος.
είναι μοναδιαία. Άρα κάπου υπάρχει λάθος.
Πώς βγάζεις για παράδειγμα αυτό που γράφεις «Cn^2*(ψ1x^2+ψ2x^2+….+ψnx^2)=Cn^2*(n-(ψ1x^2+ψ2x^2+….+ψnx^2))»; Προφανώς στο δεξί μέλος θέλεις το άθροισμα τετραγώνων των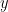 -συντεταγμένων.
-συντεταγμένων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Ιουλίου, 2015 @ 6:47 μμ
ναι στο δεξι μελος ειναι το αθροισμα των τετραγωνων των y συντεταγμενων απλα επειδη για καθε j ισχυει οτι ψjx^2+ψjy^2=1 λυνοντας ως προς ψjy εχουμε ψjy^2=1-ψjx^2 και αντικαθιστουμε…
ισως η υποθεση οτι ειναι κορυφες πολυγωνου χρειαζεται για την ισοτητα που δεν απεδειξα:
ψ1x*ψ1y+ψ2x*ψ2y+….+ψnx*ψny=0
που προκυπτει παλι απο το Α*Β=I…
για τα υπολοιπα ομως δεν χρειαζεται νομιζω πουθενα..
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 6 Ιουλίου, 2015 @ 8:07 μμ
8: Όχι, δε μπορεί να βγει αυτή η ισότητα χωρίς να χρησιμοποιήσεις κάτι παραπάνω από το ότι είναι μοναδιαία διανύσματα.
Πάρε για παράδειγμα τα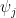 να είναι όλα πολύ κοντά στο διάνυσμα (1,0). Τότε το άθροισμα «ψ1x^2+ψ2x^2+….+ψnx^2= n/2» που γράφεις είναι σχεδόν
να είναι όλα πολύ κοντά στο διάνυσμα (1,0). Τότε το άθροισμα «ψ1x^2+ψ2x^2+….+ψnx^2= n/2» που γράφεις είναι σχεδόν  και όχι
και όχι 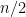 όπως γράφεις.
όπως γράφεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Ιουλίου, 2015 @ 8:24 μμ
αυτα ομως δε μας κανουν επειδη μετα το αθροισμα των τετραγωνων των y συντεταγμενων θα ειναι σχεδον 0 και εμεις θελουμε να ειναι 1… αρα μαλλον πρεπει να δειξουμε οτι οταν ειναι κορφες πολυγωνου ισχυει.. δεν ξερω ομως αν γινεται και πως.. δεν πειραζει αφηστε το..
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 6 Ιουλίου, 2015 @ 9:06 μμ
Ορίζω πίνακα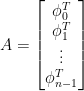 με
με ![\phi_i^T=c_n\left[cos\left(\frac{2\pi i}N\right)~~sin\left(\frac{2\pi i}N\right)\right]](https://s0.wp.com/latex.php?latex=%5Cphi_i%5ET%3Dc_n%5Cleft%5Bcos%5Cleft%28%5Cfrac%7B2%5Cpi+i%7DN%5Cright%29%7E%7Esin%5Cleft%28%5Cfrac%7B2%5Cpi+i%7DN%5Cright%29%5Cright%5D+&bg=ffffff&fg=000000&s=0&c=20201002) . Τότε
. Τότε 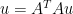 . Επομένως πρέπει
. Επομένως πρέπει 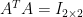 .
. είναι ορθογώνιες και επομένως ο
είναι ορθογώνιες και επομένως ο  είναι διαγώνιος, αρά αρκεί να εξασφαλιστεί ότι
είναι διαγώνιος, αρά αρκεί να εξασφαλιστεί ότι 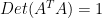 . Συγκεκριμένα,
. Συγκεκριμένα, 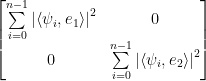 . Λόγω της συμμετρίας οι δύο διαγώνιοι όροι είναι ίσοι (γι’ αυτό και αρκεί μία σταθερά
. Λόγω της συμμετρίας οι δύο διαγώνιοι όροι είναι ίσοι (γι’ αυτό και αρκεί μία σταθερά 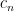 ) .
) . 
Οι στήλες του
Μου αρέσει!Μου αρέσει!
Σχόλιο από Constantinos Vrohidis — 4 Σεπτεμβρίου, 2015 @ 5:49 μμ
11: Πολύ σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Σεπτεμβρίου, 2015 @ 7:51 πμ