… και εμείς υπολογίζουμε αθροίσματα!!! Αν οι αριθμοί έχουν άθροισμα μηδέν και είναι όλοι απόλυτα φραγμένοι από μια θετική σταθερά
, τότε υπάρχει αναδιάταξη
τέτοια ώστε
για κάθε
. Το πρόβλημα πρότεινε ο Κωνσταντίνος Κουρουζίδης.
1 Ιουλίου, 2015
Εδώ ο κόσμος χάνεται…
17 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Μια μικρή τροποποίηση στη σημειογραφία: Να συμβολίσουμε την αναδιάταξη,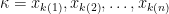 . Η πρόταση ισχύει, οποτεδήποτε δοθέντων των αριθμών
. Η πρόταση ισχύει, οποτεδήποτε δοθέντων των αριθμών  πάρουμε
πάρουμε 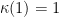 στην αναδιάταξη μας. Υπάρχει αναδιάταξη δηλαδή, έστω και αν αφήσουμε τον πρώτο όρο στην ίδια θέση.
στην αναδιάταξη μας. Υπάρχει αναδιάταξη δηλαδή, έστω και αν αφήσουμε τον πρώτο όρο στην ίδια θέση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 1 Ιουλίου, 2015 @ 9:38 μμ
Δοθέντων των αριθμών (διόρθωση ορθογραφικού)
(διόρθωση ορθογραφικού)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 1 Ιουλίου, 2015 @ 9:42 μμ
Αν κατάλαβα καλά τι ζητάμε, νομίζω ότι μια τέτοια διάταξη πρακτικά θα μπορούσε να κατασκευαστεί ως εξής:
Χωρίζουμε τους αριθμούς χ1, χ2, … , χη σε θετικούς και αρνητικούς. Αν ανάμεσά τους υπάρχουν και αριθμοί ίσοι με 0, η θέση τους μπορεί να βρίσκεται οπουδήποτε στη διάταξη. Ας υποθέσουμε λοιπόν ότι, μεταξύ των αριθμών, υπάρχουν ένας τουλάχιστον θετικός και ένας τουλάχιστον αρνητικός.
Επιλέγουμε για την πρώτη θέση έναν οποιονδήποτε αριθμό Χ1 (ή αφήνουμε τον αριθμό που ήταν πρώτος και στην αρχική διάταξη). Χ.Β.Γ. έστω 0 ≤ Χ1 ≤ c.
Επιλέγουμε για τις επόμενες θέσεις έναν ή περισσότερους αρνητικούς αριθμούς αθροίσματος Α1, έτσι ώστε να είναι: -c ≤ Χ1+Α1≤ 0. Η σειρά μεταξύ των αριθμών – όρων του αθροίσματος Α1 είναι αδιάφορη.
Επιλέγουμε για τις επόμενες θέσεις έναν ή περισσότερους θετικούς αριθμούς αθροίσματος Α2, τέτοιους ώστε να είναι: 0 ≤ Χ1+Α1+Α2 ≤ c. Η σειρά μεταξύ των αριθμών – όρων του αθροίσματος Α2 είναι αδιάφορη.
Συνεχίζουμε εναλλάξ με τον ίδιο τρόπο, μέχρι να τελειώσουν οι αριθμοί, οπότε και Χ1+Α1+Α2+..+Αν = 0.
Έτσι, τα προοδευτικά αλγεβρικά αθροίσματα των αριθμών της διάταξης, ξεκινώντας από την πρώτη θέση και φτάνοντας μέχρι οποιαδήποτε επόμενη, παραμένουν πάντα εντός του διαστήματος [-c,c].
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 15 Ιουλίου, 2015 @ 12:30 μμ
Σωστός ο αλγόριθμος εύρεσης επιθυμητής αναδιάταξης. Πρέπει να αποδείξουμε γιατί δουλεύει όμως. Μπορούμε να το κάνουμε αυτό χρησιμοποιώντας επαγωγή στα μερικά αθροίσματα. Αν έχουμε ήδη χρησιμοποιήσει μέχρι κάποιο στάδιο αριθμούς:
 που ικανοποιούν
που ικανοποιούν 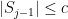 , όπου
, όπου 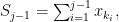 τότε μπορούμε πάντοτε να επιλέξουμε
τότε μπορούμε πάντοτε να επιλέξουμε 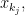 έτσι ώστε
έτσι ώστε 
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 15 Ιουλίου, 2015 @ 2:22 μμ
Ο παραπάνω ισχυρισμός χρειάζεται απόδειξη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 15 Ιουλίου, 2015 @ 2:25 μμ
Κωνσταντίνε, θα προσπαθήσω να το διατυπώσω όπως το αντιλαμβάνομαι διαισθητικά, αφήνοντας κατά μέρος την επαγωγή που προτείνεις:
Ο αλγόριθμος νομίζω πως δουλεύει διότι κάθε αριθμός χ1, χ2,..,χn βρίσκεται εξ ορισμού εντός του διαστήματος [-c,c], ενώ το προοδευτικό άθροισμα των αριθμών που έχουν τοποθετηθεί σε κάθε βήμα στη διάταξη είναι ακριβώς αντίθετο του αθροίσματος των αριθμών που δεν έχουν ακόμα τοποθετηθεί, δεδομένου ότι χ1+χ2+..+χη = 0, εξ ορισμού επίσης.
Αν επομένως το ‘τοποθετημένο’ άθροισμα σε οποιοδήποτε βήμα του αλγορίθμου βρίσκεται στο ένα μισό (στη μεριά του + ή τη μεριά του -) του διαστήματος [-c,c], τότε το ΄μη τοποθετημένο’ άθροισμα θα βρίσκεται στην ακριβώς συμμετρική θέση στην άλλη μεριά. Αναγκαστικά, νομίζω ότι μέχρι να τελειώσουν οι αριθμοί, θα υπάρχει πάντα ένας τουλάχιστον ή ένα μπλοκ μη τοποθετημένων αριθμών, που μπορούν στο επόμενο βήμα να ανατρέπουν, εντός των ορίων του [-c,c] και να ισορροπούν / μηδενίζουν τελικά τη ζυγαριά του προοδευτικού αθροίσματος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 15 Ιουλίου, 2015 @ 3:42 μμ
Σωστή η απόδειξη. Η συνθήκη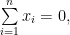 είναι ικανή αλλά όχι αναγκαία. Μπορούμε να δείξουμε το ισχυρότερο, ότι αρκεί
είναι ικανή αλλά όχι αναγκαία. Μπορούμε να δείξουμε το ισχυρότερο, ότι αρκεί 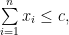 για να υπάρχει η επιθυμητή αναδιάταξη;
για να υπάρχει η επιθυμητή αναδιάταξη;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 15 Ιουλίου, 2015 @ 4:27 μμ
Στο νέο ερώτημα, εννοείται ότι όλοι οι αριθμοί παραμένουν απόλυτα φραγμένοι από μια σταθερά που επιλέγουμε πάντοτε να είναι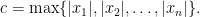
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 15 Ιουλίου, 2015 @ 4:48 μμ
Νομίζω ότι η συνθήκη Σxi ≤ c δεν αρκεί, αν συμβαίνει να είναι και Σxi ≤ -c.
Εκτός κι αν εννοείς ότι η νέα συνθήκη είναι η │Σxi│ ≤ c.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 17 Ιουλίου, 2015 @ 12:57 μμ
Έχεις δίκαιο Θανάση. Η απόλυτη τιμή του όλου αθροίσματος να φράσσεται από το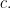 Έχω μια απόδειξη βασισμένη στην επαγωγή που αναφέρω στο 4. Νομίζω μπορεί να αποδειχθεί και με γενίκευση της δικής σου προσέγγισης αν και πιστεύω είναι δύσκολο να είναι κανείς ακριβής-καλά περιγραφικός με αυτό το πρόβλημα χρησιμοποιώντας τη μέθοδο αυτή.
Έχω μια απόδειξη βασισμένη στην επαγωγή που αναφέρω στο 4. Νομίζω μπορεί να αποδειχθεί και με γενίκευση της δικής σου προσέγγισης αν και πιστεύω είναι δύσκολο να είναι κανείς ακριβής-καλά περιγραφικός με αυτό το πρόβλημα χρησιμοποιώντας τη μέθοδο αυτή.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 17 Ιουλίου, 2015 @ 1:51 μμ
Εντάξει Κωνσταντίνε, είμαστε σύμφωνοι. Ναι, νομίζω ότι η ίδια διαισθητική προσέγγιση θα δούλευε κι εδώ: φορτώνουμε εναλλάξ πακέτα θετικών και αρνητικών αριθμών όσο γίνεται μεγαλύτερου απόλυτου αθροίσματος κάθε φορά, αλλά πάντα κρατώντας το τοποθετημένο άθροισμα εντός του διαστήματος [-c,c], μέχρι να μας τελειώσουν οι αριθμοί.
Δεν θα κουράσω όμως άλλο με λεπτομέρειες και θα περιμένω να δω, από εσένα ή κάποιον άλλο φίλο, την αυστηρή επαγωγική απόδειξη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 17 Ιουλίου, 2015 @ 2:16 μμ
Ας την δούμε. Αν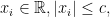 και
και 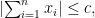 τότε υπάρχει αναδιάταξη
τότε υπάρχει αναδιάταξη 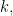 τέτοια ώστε
τέτοια ώστε  και
και
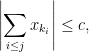 για κάθε
για κάθε 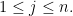 Απόδειξη πάνω στο στάδιο των μερικών αθροισμάτων
Απόδειξη πάνω στο στάδιο των μερικών αθροισμάτων  Χωρίς βλάβη μπορούμε να υποθέσουμε ότι
Χωρίς βλάβη μπορούμε να υποθέσουμε ότι
 ειδάλλως αντιστρέφουμε τα πρόσημα όλων των
ειδάλλως αντιστρέφουμε τα πρόσημα όλων των  Για
Για  παίρνουμε απλά τον πρώτο όρο στη λίστα των αριθμών που έχουμε, να είναι ο πρώτος όρος στην αναδιάταξή μας και η πρόταση ισχύει βεβαίως. Αρκεί να δείξουμε ότι αν έχουμε ήδη επιλέξει:
παίρνουμε απλά τον πρώτο όρο στη λίστα των αριθμών που έχουμε, να είναι ο πρώτος όρος στην αναδιάταξή μας και η πρόταση ισχύει βεβαίως. Αρκεί να δείξουμε ότι αν έχουμε ήδη επιλέξει:  αναδιατεταγμένους αριθμούς δηλαδή από τη λίστα μας που ικανοποιούν
αναδιατεταγμένους αριθμούς δηλαδή από τη λίστα μας που ικανοποιούν 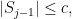 όπου
όπου 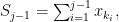 τότε μπορούμε πάντοτε να επιλέξουμε
τότε μπορούμε πάντοτε να επιλέξουμε 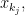 έτσι ώστε
έτσι ώστε  Ας ονομάσουμε το
Ας ονομάσουμε το 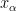 «ελεύθερον» (είναι ένα από τα
«ελεύθερον» (είναι ένα από τα 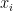 ) εάν
) εάν  Επιλέγουμε
Επιλέγουμε 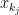 με τον ακόλουθο κανόνα:
με τον ακόλουθο κανόνα: και υπάρχει ελεύθερον
και υπάρχει ελεύθερον  θέτουμε
θέτουμε  Δουλεύει αφού
Δουλεύει αφού 
 και όλα τα ελεύθερα
και όλα τα ελεύθερα 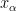 είναι θετικά, μπορούμε να επιλέξουμε οποιοδήποτε, αφού
είναι θετικά, μπορούμε να επιλέξουμε οποιοδήποτε, αφού 
 και υπάρχει ελεύθερον
και υπάρχει ελεύθερον  θέτουμε
θέτουμε  Δουλεύει αφού
Δουλεύει αφού 
 με όλα ελεύθερα
με όλα ελεύθερα  (να είναι όλα αρνητικά), είναι αδύνατον από την υπόθεση που κάναμε αρχικά
(να είναι όλα αρνητικά), είναι αδύνατον από την υπόθεση που κάναμε αρχικά 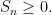
(1) Εάν
(2) Εάν
(3) Εάν
Μένει να παρατηρήσουμε ότι στην περίπτωση
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 17 Ιουλίου, 2015 @ 3:40 μμ
Στην υπόθεση, χωρίς βλάβη για το δεν έπρεπε να βάλω απόλυτες τιμές.
δεν έπρεπε να βάλω απόλυτες τιμές.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 17 Ιουλίου, 2015 @ 4:21 μμ
Ευχαριστώ Κωνσταντίνε, εξαιρετική (και ομολογώ καθόλου κουραστική) η απόδειξή σου!
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 17 Ιουλίου, 2015 @ 4:23 μμ
Δεν είναι δική μου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 17 Ιουλίου, 2015 @ 4:32 μμ
Σε τιμά να το λες! Υπάρχει μήπως τίποτε δικό μας; 🙂 Την παρουσίασες πάντως άψογα, κατά τη γνώμη μου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 17 Ιουλίου, 2015 @ 4:44 μμ
Αυτή η άσκηση είναι το λήμμα 3.1 που βρίσκεται στο άρθρο του οποίου η διεύθυνση-link είναι στο πρόβλημα: Διάσπαση ακολουθίας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 14 Φεβρουαρίου, 2019 @ 10:15 μμ