Έχουμε 1000 κουτιά στη σειρά (στις θέσεις 1, 2, 3, … , 1000).
Δείξτε ότι μπορούμε να τα βάψουμε με δύο χρώματα, π.χ. κόκκινα ή μπλε, με τέτοιο τρόπο ώστε να μην υπάρχει αριθμητική πρόοδος μήκους 20 από κουτιά που να είναι όλα το ίδιο χρώμα.
RSS feed for comments on this post. TrackBack URI
 | Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… |
 | Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; |
 | George Rizopulos στη Μπορείτε να σκοτώσετε τον… |
 | Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
 | ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.
Προβλήματα Μαθηματικών 
Μιχάλη, όταν γράφεις «αριθμητική πρόοδος μήκους 20» εννοείς μια αρ. πρόοδο με 20 όρους;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 26 Ιουνίου, 2015 @ 7:28 μμ
Υποθέτω ότι το «δείξτε ότι μπορούμε να τα βάψουμε» δηλώνει ότι το ζητούμενο είναι μόνο να αποδειχθεί ότι υπάρχει ο τρόπος . Ή ζητείται ΚΑΙ ο τρόπος βαφής;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 26 Ιουνίου, 2015 @ 7:37 μμ
αν καταλαβα σωστα το προβλημα θα μπορουσαμε να τα χρωματισουμε ως εξης:
>(1*κοκκινο+1*μπλε)*19 φορες (δηλαδη 2*19=38 κουτια)
>(2*κοκκινο+2*μπλε)*19 φορες (δηλαδη 4*19=76 κουτια)
>(3*κοκκινο+3*μπλε)*19 φορες (δηλαδη 6*19=114 κουτια)
>(4*κοκκινο+4*μπλε)*19 φορες (δηλαδη 8*19=152 κουτια)
και συνεχιζουμε ετσι μεχρι να φτασουμε τα 1000 κουτια συνολικα.. και εχουμε 1000/19=52 περιπου ακολουθιες απο α*κοκκινα+α*μπλε κουτια οπου η καθε ακολουθια εχει 2α*19 κουτια.. αρα για να μην εχουμε αριθμητικη προοδο μηκους 20 πρεπει α<20 που ισχυει γιατι για να φτασουμε στο 1000 αφου 1000=19*52 περιπου και αρα 1000<19*56 και 56=2+2*2+2*3+2*4+2*5+2*6+2*7 , δηλαδη μεγιστο α=7<20
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 26 Ιουνίου, 2015 @ 7:46 μμ
1,2: Ναι, εννοώ ΑΠ με 20 όρους. Αρκεί να αποδειχτεί ότι υπάρχει ο χρωματισμός. Δε χρειάζεται να το κατασκευάσετε, αλλά, φυσικά, μια κατασκευή είναι πάντα ευπρόσδεκτη.
3. Μια ΑΠ με 20 όρους μπορεί να αρχίζει με οποιοδήποτε αριθμό και να έχει οποιοδήποτε βήμα. Είναι δηλ. οι όροι,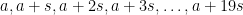
όπου οι ακέραιοι 
μπορεί να είναι οποιοιδήποτε φτάνει και οι 20 παραπάνω όροι να είναι από 1 έως 1000. Θα πρέπει να μας αποδείξεις ότι ο χρωματισμός που προτείνεις δεν «μονοχρωματίζει» οποιαδήποτε τέτοια ΑΠ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 26 Ιουνίου, 2015 @ 8:02 μμ
Όλοι οι δυνατοί συνδυασμοί χρωμάτων στα 1000 κουτιά ,είναι 2^1000.
Οι δυνατοί χρωματισμοί των {α,α+s, a+2s, …,a+19s} είναι 2 * 2^980. Αυτό επειδή η κάθε 20άδα έχει 2 επιλογές χρώματος (κόκκινο-μπλε) και μένουν 2 επιλογές (κοκ-μπλε) για καθένα από τα εναπομείναντα 1000-20=980 κουτιά (από τα 1000 κάθε φορά). (2 * 2^980)/2^1000= 1/2^19 .Ένας στους 2^19 συνδυασμούς.
Πόσα ζεύγη όμως α και s υπάρχουν;
α+19s <ή ίσο 1000
άρα α<1000 και s<1000/19
(1000^2)/19 < 2^19 (πολύ μικρότερο μάλιστα! είναι μικρότερο και από 2^16 . Αρα μπορούμε να βελτιώσουμε το 20 σε 17. αρ.πρόοδο μήκους 17)
Δεν ξέρω αν στέκει φορμαλιστικά αυτή η πιθανοτική προσέγγιση (λογική "συχνότητας"), αλλά μου φαίνεται λογική.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 26 Ιουνίου, 2015 @ 8:27 μμ
ααα αρα λαθος… τωρα νομιζω καταλαβα…
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 26 Ιουνίου, 2015 @ 8:48 μμ
Νομίζω ότι το συνδυαστικό επιχείρημα καταμέτρησης στο 5. στέκει μια χαρά. Αφού η ένωση όλων των δυνατών χρωματισμών διαδοχικών 20 άδων είναι μικρότερη από το δειγματικό χώρο (2^1000) υπάρχουν στοιχεία αυτού του δειγμ.χώρου που δεν κείνται στην ένωση. ΟΕΔ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 26 Ιουνίου, 2015 @ 9:35 μμ
5,7: Δεν αρνούμαι ότι το επιχείρημά σου δουλεύει αλλά όπως είναι γραμμένο δεν το καταλαβαίνω. Μπορείς να το εξηγήσεις λίγο παραπάνω; Δηλ., τι ακριβώς μετράμε, ποιο σύνολο είναι μεγαλύτερο από ποιο, κλπ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 26 Ιουνίου, 2015 @ 11:32 μμ
@8. Mιχάλη, αυτό που λέω είναι το εξής: Πόσοι είναι όλοι οι δυνατοί χρωματισμοί των 1000 κουτιών; Απ: 2^1000. Αυτός ο αριθμός συνιστά έναν -ας τον πούμε- δειγματικό χώρο Ω. Πόσοι είναι οι δυνατοί χρωματισμοί μιας ακολουθίας /20άδας; 2^981 (για το λόγο που αναφέρω στο 5.)
Αν λοιπόν ο αριθμός, το πλήθος των 20άδων είναι 2^19 ,τότε ο Ω «γεμίζει» από αυτές και δεν υπάρχει κανένας συνδυασμός από τους 2^1000 που να αντιστοιχεί στον τρόπο βαψίματος που θέλουμε. Δηλαδή θα υπάρχει οπωσδήποτε τέτοια ακολουθία.
Η ανισότητα όμως a+19s<=1000 (με τους εύκολους υπολογισμούς στο 5.) δείχνει ότι αυτό το πλήθος είναι < 2^19.
Άρα υπάρχει "κενό" στον Ω, το οποίο κενό αντιστοιχεί αναγκαστικά σε ακολουθίες 1000 κουτιών χωρίς να υπάρχει αρ.πρόοδος μήκους 20.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 27 Ιουνίου, 2015 @ 7:37 πμ
Ουσιαστικά δηλαδή, δείξαμε ότι η πιθανότητα να επιλέξω τυχαία (από μία ομοιόμορφη κατανομή χρωματισμών των 1000 κουτιών) 1 χρωματισμό και αυτός να περιέχει ακολουθία κουτιών με την ιδιότητα που θέλουμε , είναι αυστηρώς < 1.
Νομίζω ότι δεν είναι συνήθιστη αυτή η "πιθανοτική μέθοδος" λέγεται; σε θέματα Θεωρίας Αριθμών. Αν δεν με προδίδει ο Αλτσχάιμερ ο Έρντος και ο Ράντο στήριξαν πολλά θεωρήματα έτσι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 27 Ιουνίου, 2015 @ 7:45 πμ
9,10: Σωστά. Αυτή είναι όντως μια «πιθανοτική απόδειξη». Δείτε και το πολύ σχετικό πρόβλημα εδώ.
Έχω μόνο αντίρρηση σε αυτό που γράφεις «Αν λοιπόν ο αριθμός, το πλήθος των 20άδων είναι 2^19 ,τότε ο Ω «γεμίζει» από αυτές και δεν υπάρχει κανένας συνδυασμός από τους 2^1000 που να αντιστοιχεί στον τρόπο βαψίματος που θέλουμε.» Αυτό δεν είναι σωστό. Δε σημαίνει δηλ. ότι σε αυτή την περίπτωση δε θα υπήρχε λύση, σημαίνει απλά ότι η μέθοδος δε δουλεύει. Ο λόγος είναι ότι οι χρωματισμοί που χρωματίζουν κόκκινη μια ΑΠ και οι χρωματισμοί που χρωματίζουν π.χ. μπλε μια άλλη ΑΠ δεν είναι απαραίτητα διαφορετικοί και δε δικαιούσαι να τους προσθέσεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Ιουνίου, 2015 @ 8:21 πμ
11. Α, έχεις δίκιο! Moυ διέφυγε το inclusion-exclusion του θέματος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 27 Ιουνίου, 2015 @ 9:25 πμ
12. Nα διευκρινίσουμε όμως ότι η «συμπερίληψη» ίδιων καταστάσεων χρωματισμών ,απλώς ενισχύει το συμπέρασμα του 5. & 10. αφού αν αφαιρέσουμε τις ίδιες, ο Ω αδειάζει ακόμη περισσότερο. Σωστά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 27 Ιουνίου, 2015 @ 11:38 πμ
13: Σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Ιουνίου, 2015 @ 7:09 μμ
Ποιος είναι ο μικρότερος αριθμός κουτιών
που να είμαστε σίγουροι ότι υπάρχει ΑΠ με 20 όρους σε κάθε χρωματισμό (με 2 χρώματα) των 
κουτιών; Υπάρχει πιο αποτελεσματικός τρόπος να βρεθεί παρά με exhaustive search;
Ευχαριστώ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 30 Ιουνίου, 2015 @ 9:34 μμ
15: Οι αριθμοί αυτοί είναι γενικά πάρα πολύ δύσκολο να βρεθούν ακόμη και για πολύ μικρότερα νούμερα. Το exhaustive search πρακτικά δε μπορεί κανείς να το χρησιμοποιήσει για μεγάλα νούμερα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 30 Ιουνίου, 2015 @ 9:48 μμ