Προβλήματα Μαθηματικών

19 Ιουνίου, 2015

Μπάλες σε χρωματιστά κουτιά

Filed under: Λυμένα Προβλήματα — Mihalis Kolountzakis @ 10:05 πμ

f

Έχουμε n αριθμημένες μπάλες (n>2) και κάμποσα, επίσης αριθμημένα, χρωματιστά κουτιά, κάποια από τα οποία είναι βαμμένα κόκκινα, κάποια μπλε και κάποια είναι άβαφα (υπάρχουν και από τα τρία είδη κουτιών).

Ας είναι A το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθετηθούν αποκλειστικά στα άβαφα κουτιά και B το πλήθος των τρόπων με τους οποίους μπορούν αυτές οι μπάλες να τοποθτηθούν σε κουτιά που είναι όλα του ίδιου χρώματος (κόκκινου ή μπλε).

Δείξτε ότι πάντα A \neq B.

25 Σχόλια »

  1. H εφώνηση είναι ασαφής. Λόγου χάρη, τα κουτιά είναι διακριτά ή όχι;Είναι διατεταγμένα ή όχι; Οι μεταθέσεις (permutations) λαμβάνονται υπόψι ή όχι;
    Ας πούμε, αν έχω 3 κουτιά, 1 κόκκινο, 1 μπλε, 1 άβαφο και 3 μπάλες ,υπάρχει ένας τρόπος να βάλω 1 μπάλα σε κάθε κουτί; ή περισσότεροι; Οι μπάλες υποθέτω πως είναι indistinguishable. Πρέπει σε κάθε κουτί να υπάρχει τουλάχιστον μία μπάλα σε κάθε διανομή, ή όχι;

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 11:05 πμ

  2. Και οι μπάλες και τα κουτιά είναι αριθμημένα (δηλ., έχουν ονόματα, είναι διαφορετικά το ένα από το άλλο). Κατά τα άλλα ό,τι δεν απαγορεύεται από την εκφώνηση επιτρέπεται.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 11:12 πμ

  3. 2. Eυχαριστώ για τις διευκρινίσεις . Τώρα εξηγείται και το πολύ ωραίο «κεκαλυμμένο» hint με την εικόνα του καλού μας νομικού Πετράκη.
    Έχουμε λοιπόν,στο προκείμενο, να διανείμουμε κ διακριτές (distinguishabe ,ή αλλιώς εκφρασμένο «αριθμημένες/με όνομα») μπάλες σε ν διακριτά κουτιά.
    Δεν υπάρχει περιορισμός στον αριθμό από μπάλες που μπορεί να έχει κάθε κουτί.
    Μπορούμε να πούμε πως το πρόβλημα είναι ισοδύναμο με το να επιλέξουμε κ από τα ν κουτιά, με το κάθε κουτί φυσικά να μπορεί να επιλεγεί περισσότερες από μια φορές.
    Ήτοι, με ορολογία Συνδυαστικής πλέον, έχουμε να κάνουμε με διατεταγμένες επιλογές (ordered selections) ή όπως είναι ευρύτερα γνωστές ,με «μεταθέσεις» (permutations) των κουτιών με απεριόριστες επαναλήψεις.
    Υπάρχει το εξής σχετικό θεώρημα (η απόδειξή του είναι εξειραετικά απλή. Επιφυλάσσομαι…)
    Η διανομή κ διακριτών μπαλών σε ν διακριτά κουτιά,χωρίς exclusion (δηλαδή τον περιορισμό 1 μπάλα ανά κουτί) , αντιστοιχεί στο να φτιάξουμε μία μετάθεση μεγέθους(πληθαρίθμου) κ , με απεριόριστες επαναλήψεις (unrestricted repetitions), από ένα σύνολο μεγέθους ν. Γι’αυτό , υπάρχουν ν^κ διαφορετικοί τρόποι να διανείμουμε κ διαφορετικές /διακριτές μπάλες σε ν διακριτά κουτιά , με τυχαίο αριθμό μπαλών ανα κουτί.
    Τώρα , πρέπει να λύσουμε μια εξίσωση της μορφής …ας ρωτήσουμε όμως τον κύριο της εικόνας καλύτερα , γιατί η καθαρή Συνδυαστική τελείωσε και με την Άλγεβρα ψιλομπερδεύομαι…

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 12:57 μμ

  4. Mάλλον βιάστηκα. Να αγνοηθεί το 3. προς το παρόν.

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 3:06 μμ

  5. Οκ. Καλά τα είπα στο 3. η αδυναμία λύσης της ν^κ =μ^κ + λ^κ (στους φυσικούς >2) δείχνει το ζητούμενο. Vive αυτός που έγραφε σε πακέτα από τσιγάρα και περιθώρια αλλόκοτων λατινικών μεταφράσεων από τα ελληνικά!

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 3:49 μμ

  6. 3: Γράφεις » Γι’αυτό , υπάρχουν ν^κ διαφορετικοί τρόποι να διανείμουμε κ διαφορετικές /διακριτές μπάλες σε ν διακριτά κουτιά , με τυχαίο αριθμό μπαλών ανα κουτί. «.

    Δε διαφωνώ, αλλά γιατί;

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 4:59 μμ

  7. 6. Mιχάλη, ευχαρίστως να το κάνω. Δεδομένου ότι ισχύει αυτό, τα υπόλοιπα είναι οκ;

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 5:07 μμ

  8. Ναι, το πρόβλημα είναι απλά το τελευταίο θεώρημα του Fermat σε συγκεκαλυμμένη μορφή, και αποδεικνύεται ανάγοντάς το σε αυτό.

    Η πρόταση παραπάνω είναι πραγματικά πολύ απλή για να μη συμπεριλάβει κανείς την απόδειξή της.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 5:08 μμ

  9. Οκ. λοιπόν. Συγχαρητήρια καταρχάς για την ωραία ιδέα της σύνδεσης τού Φερμά με το προκείμενο!
    Θα δώσω μια ελάχιστα φορμαλιστική προσέγγιση αλλά πολύ κατανοητή θεωρώ.
    Ας υποθέσουμε ότι έχουμε να βάλουμε ν διακριτές μπάλες σε ν διακριτά κουτιά.
    Πόυ μπορεί να πάει η μπάλα με τον υποθετικό αριθμό 1 πάνω της; Όπου θέλει! Δηλαδή ν επιλογές για την μπάλα νο. 1
    Διά ΚΑΘΕ τρόπο επιλογής τού πού πάει η νο.1, υπάρχουν ν επιλογές για το πού θα πάει η μπαλα νο.2
    Υπάρχουν λοιπόν ν*ν=ν^2 επιλογές για τη μοίρα των νο.1 και νο.2
    Καταλαβαίνουμε ότι δεν αλλάζει κάτι για την μπάλα νο.3 , κ.λ.π. Για κάθε επιλογή από τις ν^2 υπάρχουν ν επιλογές για την νο.3. άρα ν^3 ,κ.λ.π.
    Δεν αλλάζει προφανώς κάτι αν γενικεύσουμε για ν μπάλες και κ κουτιά. Σε κάθε στάδιο «δυνατών επιλογών» διαθέτουμε κ δυνατές αποφάσεις, ήτοι κ^ν στο σύνολο.

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 19 Ιουνίου, 2015 @ 5:19 μμ

  10. 9: Τέλεια.

    Πάντως δεν είναι δικιά μου η σύνδεση.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 5:20 μμ

  11. Δεν τα κατάφερα δυστυχώς να βρεθώ νωρίτερα σε αυτή την (ακόμα μία) τελετή μνήμης για το Φερμά, αλλά ο Γ.Ριζόπουλος τον τίμησε τόσο καλά και με το παραπάνω, ώστε οι όποιες απουσίες να μένουν απαρατήρητες. Τα μπράβο μου στο φίλο Γιώργη και το θαυμασμό μου φυσικά στον αγαπητό Μιχάλη για το ωραίο πρόβλημα!. Αναρωτιέμαι μόνο αν ο Φερμά, που ήταν εκτός των πολλών άλλων και βασικός θεμελιωτής της θεωρίας των πιθανοτήτων, ήξερε ή μπορούσε να φανταστεί αυτή την ωραία εφαρμογή του τελευταίου θεωρήματός του.
    Ήθελα με την ευκαιρία να κάνω και μια παρατήρηση για το ίδιο το πρόβλημα: αν ζητούσαμε σε κάθε κουτί να μπαίνει και μία το πολύ μπάλα, οπότε θα χρειαζόμασταν να υπάρχουν από κάθε χρώμα τόσα τουλάχιστον κουτιά όσα και οι μπάλες, θα εξακολουθούσε να ισχύει πάντα η ίδια ανισότητα; Άποψή μου είναι ότι ναι και η απόδειξη νομίζω ότι δεν περνάει από το τελευταίο θεώρημα του Φερμά,, αλλά χωράει στο περιθώριο μιας σελίδας :-).

    Μου αρέσει!

    Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 20 Ιουνίου, 2015 @ 4:27 μμ

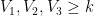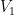  12. Χαίρετε. Νομίζω το νέο πρόβλημα που έθεσε ο Θανάσης ανάγετε στον αν η εξίσωση: \binom {V_1}{k} \cdot k!=\binom {V_2}{k} \cdot k! + \binom {V_3}{k} \cdot k! έχει λύση για οποιουσδήποτε φυσικούς V_1, V_2, V_3 \geq k. Έχουμε δηλαδή k διακριτές μπάλες και τα κουτιά μας (π.χ. V_1, είναι ο αριθμός των αβάφων). Επειδή το πολύ μια μπάλα μπορεί να μπει σε κάθε κουτί, και όλα είναι διακριτά, ο διωνυμικός συντελεστής μας δίνει τον αριθμό των υποσυνόλων μεγέθους k από ένα μεγαλύτερο σύνολο (ήτοι του αριθμού κάποιου από των κουτιών) και ο πολλαπλασιασμός με k! 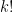μετράει τις μεταθέσεις των μπαλών στα κουτιά (τα οποία είναι διακεκριμένα).

    Μου αρέσει!

    Σχόλιο από Κωνσταντίνος Κουρουζίδης — 20 Ιουνίου, 2015 @ 9:42 μμ

  13. Σωστό Κωνσταντίνε. Ή αλλιώς: κ!(κ-ν)!
    Υπάρχουν k(k-1)(k-2)…(k-n+1)=k!/(k-n)! το οποίο εξηγείται εποπτικά με το να πουμε υπαρχουν κ επιλογές για την 1η μπάλα, κ-1 για τη 2η κ.λ.π. ή αλλιώς με το «διάταξε με όλους τους τρόπους τα κουτιά (ν! τρόποι) αλλά αγνόησε τα αχρησιμοποίητα κ-ν εξ’αυτών (άρα διαίρεσε με το (κ-ν)!

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 8:38 πμ

  14. 12, 13: Συγγνώμη παιδιά. Δεν το καταλαβαίνω.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 21 Ιουνίου, 2015 @ 9:08 πμ

  15. Mιχάλη, ο Θανάσης θέτει το πρόβλημα ν διακριτές μπάλες σε κ διακριτά κουτιά με το πολύ 1 μπάλα ανα κουτί, οκ;
    Αν ν οι μπάλες υπάρχουν: ν επιλογές για το 1ο κουτί, ν-1 για το 2ο κ.ο.κ.
    ν*(ν-1)*(ν-2)*…*(ν-κ+1)= ν!/(ν-κ)! που είναι ο ίδιος τύπος ουσιαστικά με αυτόν που έχει ο Κουρουζίδης.

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 9:17 πμ

  16. Α, στο 13 διατύπωσα μπερδεμένα μπάλες και κουτιά, σόρυ

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 9:18 πμ

  17. OK, τώρα κατάλαβα τι γράφει στο 12. Νόμιζα ότι περιγράφατε τη λύση και όχι μια αναγωγή.

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 21 Ιουνίου, 2015 @ 9:28 πμ

  18. Μάλλον δεν ισχύει:

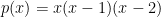    Για 3 μπάλες θα πρέπει να ισχύει p(a) \neq p(b)+p(c) για κάθε a, b, c \ge 3 όπου p(x) = x(x-1)(x-2), αν κατάλαβα καλά το συλλογισμό παραπάνω.

    Όμως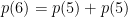 p(6) = p(5)+p(5) (120=60+60).

    Έχω καταλάβει κάτι λάθος;

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 21 Ιουνίου, 2015 @ 10:04 πμ

  19. Πολύ σωστά κατάλαβες, αγαπητέ Μιχάλη! Προφανώς δεν ισχύει και η διάψευση δε χρειάστηκε ούτε μια γραμμή από το περιθώριο! 🙂

    Μου αρέσει!

    Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 21 Ιουνίου, 2015 @ 10:24 πμ

  20. Whoaaoo! Δηλαδή την παραλλαγή Παπαδημητρίου, τελικά την έλυσε ο Κολουντζάκης! 🙂
    (σε λίγο θα ζητήσουμε και κανα ποσοστό απ’το μισθό σου, κύριε Καθηγητά!… 😆 )

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 10:39 πμ

  21. 20. (συνέχεια) Δε μού λύνεις και τα απεριοδικά πλακάκια, γιατί ζαλίζομαι ελαφρώς ;… (στείλτα στο μέηλ κι εγώ θα τα ποστάρω σαν δικά μου! 😆 )

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 11:12 πμ

  22. Οφείλω μια απολογία για το μικρό unfair στο σχόλιο 11. Όταν πρωτοδιάβασα το πρόβλημα, η ερμηνεία που έδωσα ήταν αυτή της μιας το πολύ μπάλας σε κάθε κουτί και έχοντας βρει μάλλον εύκολα τη διάψευση της ανισότητας, πήρα φόρα για να κατατροπώσω το Μιχάλη (συγγνώμη για το θράσος, αγαπητέ μου καθηγητή), αλλά μπαίνοντας στα σχόλια έπεσα στους ογκόλιθους Φερμά και Ριζόπουλο. Σκέφτηκα λοιπόν ότι θα άξιζε ίσως να θέσω στη συζήτηση και αυτή την εκδοχή.
    Θα προσθέσω στο παράδειγμα του Μιχάλη, που είναι και η απλούστερη περίπτωση της ισότητας, ότι αυτή ισχύει γενικότερα και σε όλες τις περιπτώσεις με ν>2 μπάλες και 2ν άβαφα, 2ν-1 κόκκινα και 2ν-1 μπλε κουτιά. Για να μπουν όλες οι μπάλες στα άβαφα κουτιά υπάρχουν Α=2ν(2ν-1)(2ν-2)….(ν+1) τρόποι ενώ για να μπουν όλες στα κόκκινα ή όλες στα μπλε κουτιά υπάρχουν Β =2*[(2ν-1)(2ν-2)….(ν+1)ν] τρόποι και Α=Β.

    Μου αρέσει!

    Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 21 Ιουνίου, 2015 @ 3:22 μμ

  23. 22. Ωραίος Θανάση! (αλλά μην τα πετάς απότομα αυτά τα αγγωνάρια..εεε.. τους ογκόλιθους, ήθελα να πω… 🙂 ) Άκου «στους ογκόλιθους Φερμά και Ριζόπουλο» !! 😳 Θα πέσει φωτιά να μας ρίξει σε «κατάβαση επ’άπειρον*» κουμπάρε! 🙂
    *infinite descent

    Μου αρέσει!

    Σχόλιο από George Rizopulos — 21 Ιουνίου, 2015 @ 4:09 μμ

  24. Χαίρομαι που το διασκεδάζετε.

    Πάντως η φαντασία η δικιά μου δεν είναι τόσο καλή ώστε να ανακαλύψω το αντιπαράδειγμα σκεφτόμενος.

    Ζώντας όμως στην εποχή μου, έκανα το παρακάτω:

    def f(x):
    return x*(x-1)*(x-2)

N=20

ff = {}
for x in range(3,N+1):
    y=f(x)
    if y not in ff:
        ff[y] = x

for x in ff:
    for y in ff:
        if y>x:
            continue
        if x+y in ff:
            print "{va}={vb}+{vc}, or f({a})=f({b})+f({c})".format(va=x+y, vb=x, vc=y, a=ff[x+y], b=ff[x], c=ff[y])

    με αποτέλεσμα το:

    4080=3360+720, or f(17)=f(16)+f(10)
120=60+60, or f(6)=f(5)+f(5)

    Μου αρέσει!

    Σχόλιο από Mihalis Kolountzakis — 21 Ιουνίου, 2015 @ 5:57 μμ

  25. 23. Γιώργη, με παρεξήγησες φοβάμαι. Η αναφορά στα ονόματα δεν είχε στοιχείο αξιολόγησης ή σύγκρισης και η επιλογή σειράς ήταν απολύτως χρονολογική. 🙂

    24. Μιχάλη, πολύ ωραίο και μας έδωσε και άλλο, πιο σγουρό, αντιπαράδειγμα. Αναρωτιέμαι τώρα, αν μπορείς να είσαι τόσο αποτελεσματικός μη σκεπτόμενος, τι μπορείς να καταφέρεις σκεπτόμενος! 🙂

    Μου αρέσει!

    Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 21 Ιουνίου, 2015 @ 11:38 μμ


RSS feed for comments on this post. TrackBack URI

Σχολιάστε

Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.