Στο φετινό φεστιβάλ στα Μάταλα ένας από τους πλανόδιους πωλητές χειροποίητης τέχνης θα πουλάει το μαγικό κολιέ των χρωμάτων:
Το κολιέ αυτό έχει την παρακάτω μαγική ιδιότητα που, σύμφωνα με τον πλανόδιο έμπορο, βοηθάει στο να περνάει η ζωή πιο ωραία και με λιγότερες βαρετές επαναλήψεις.
Είναι φτιαγμένο από 64 χάντρες από 8 διαφορετικά χρώματα και είναι βαλμένες αυτές με τέτοιο τρόπο ώστε αν κανείς διανύσει το μήκος του κολιέ κατά τη μια κατεύθυνση (οποιαδήποτε από τις δύο) τότε θα δει όλες τις δυνατές διαδοχές δύο χρωμάτων ακριβώς μια φορά την κάθε μία.
(Αν ονομάσουμε, χάριν συντομίας, τα χρώματά μας 
Υπάρχει τρόπος να φτιαχτεί τέτοιο κολιέ; Αν ναι, πώς; Αν όχι, γιατί;
Προβλήματα Μαθηματικών 
Μια διευκρίνιση: Δεν μετρήσατε διαβάσεις από ίδιο χρώμα σε ίδιο, 2 φορές; (στον υπολογισμό του 64) Καθώς διανύουμε το μήκος του, είναι διαφορετική η μετάβαση π.χ. κόκκινο – μπλέ, μπλέ – κόκκινο.
Αυτό όμως δεν ισχύει σε μεταβάσεις ιδίων χρωμάτων
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 17 Ιουνίου, 2015 @ 6:02 μμ
Όχι, δεν ‘έχω μετρήσει το μπλέ-μπλέ δύο φορές. Μια φορά το μπλέ-μπλέ, μια το μπλέ-κόκκινο και μια το κόκκινο-μπλέ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 6:04 μμ
Αν τα χρωματα ειναι απο το 1 εως το 8 μπορουνε να μπουν ετσι: 1-1-2-1-3-1-4-1-5-1-6-1-7-1-8-2-2-3-2-4-2-5-2-6-2-7-2-8-3-3-4-3-5-3-6-3-7-3-8-4-4-5-4-6-4-7-4-8-5-5-6-5-7-5-8-6-6-7-6-8-7-7-8-8-
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 17 Ιουνίου, 2015 @ 6:42 μμ
3: Περιμένεις να το ελέγξω με το μάτι; Αν δουλεύει γιατί και πώς το έφτιαξες;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 6:44 μμ
παει το 1 με ολα μετα το 2 με ολα εκτος το 1 που εχει παει πιο πριν μετα το 3 με ολα εκτος τα μικροτερα δηλαδη το 1 και 2 και συνεχιζει ετσι..
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 17 Ιουνίου, 2015 @ 6:50 μμ
Ωραία, κατάλαβα το πώς το φτιάχνεις, αλλά μπορείς να μας αποδείξεις ότι δουλεύει;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 7:04 μμ
εστω οτι οι μεταβασεις ειναι οι διαδες (α,β).. πρεπει λοιπον το 1 να μπει στη θεση α με ολα τα υπολοιπα στη θεση β και στη θεση β με ολα τα υπολοιπα (εκτος το 1) στη θεση α, μετα το 2 πρεπει να μπει με στη θεση α ολα τα υπολοιπα στη θεση β (εκτος το 1 που εχει ηδη μπει) και στη θεση β με ολα τα υπολοιπα στη θεση α (εκτος το 1 και το 2) κτλ… επισης οταν εχουμε την τριαδα (a, b, a) εχουμε τις δυο συμμετρικες διαδες (a,b) και (b,a).. αρα με αυτον τον τροπο εξαντλουμε ολες τις πιθανες διαδες που εχουν το 1, μετα κανουμε το ιδιο και για το 2, δηλαδη φτιαχνουμε ολες τις πιθανες διαδες που το περιεχουν εκτος απο αυτες που εχουν το 1 και φτανοντας στο 8 οι μονες διαδες που δεν εχουν γινει ειναι οι (8,8) και (8,1) που καταληγει στην αρχη… δεν ξερω τι θα καταλαβετε, δεν μπορω να το εξηγησω… :p
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 17 Ιουνίου, 2015 @ 8:10 μμ
Αν τα χρωματα ειναι οι αριθμοι 1-8, τοτε εξαντλωντας ολα τα ζευγαρια ενα ενα μπορουμε να παρουμε:
1-1-2-1-3-1-4-1-5-1-6-1-7-1-8- (15)
2-2-3-2-4-2-5-2-6-2-7-2-8- (13)
3-3-4-3-5-3-6-3-7-3-8- (11)
4-4-5-4-6-4-7-4-8- (9)
5-5-6-5-7-5-8- (7)
6-6-7-6-8- (5)
7-7-8- (3)
1 (1)
Συνολο 64. Αν και δε νομιζω ο συγκεκριμενος συνδυασμος να ειναι ωραιος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Thomas Daskalakis — 17 Ιουνίου, 2015 @ 8:32 μμ
Είναι μια ακολουθία Ντε Μπρουιν (De Bruijn)
https://en.wikipedia.org/wiki/De_Bruijn_sequence¨
για k=8, n=2. («αλφάβητο» 8 γραμμάτων με string length 2)
0 0 1 0 2 0 3 0 4 0 5 0 6 0 7 1 1 2 1 3 1 4 1 5 1 6 1 7 2 2 3 2 4 2 5 2 6 2 7 3 3 4 3 5 3 6 3 7 4 4 5 4 6 4 7 5 5 6 5 7 6 6 7 7 (0)
To τελευταίο μηδενικό σε παρένθεση δίνει το «kle;isimo» (wrap) που υπολογίζεται από το k^n +(n-1)=8^2 +(2-1)=65
πιο «τακτοποιημενα»:
0
0 1
0 2
0 3
0 4
0 5
0 6
0 7
1
1 2
1 3
1 4
1 5
1 6
1 7
2
2 3
2 4
2 5
2 6
2 7
3
3 4
3 5
3 6
3 7
4
4 5
4 6
4 7
5
5 6
5 7
6
6 7
7
Π.χ για 8 χρώματα και τριάδες (αντί για δυάδες) θα θέλαμε κ^n=8^3=512 χάντρες Ματάλων:
0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 6 0 0 7 0 1 1 0 1 2 0 1 3 0 1 4 0 1 5 0 1 6 0 1 7 0 2 1 0 2 2 0 2 3 0 2 4 0 2 5 0 2 6 0 2 7 0 3 1 0 3 2 0 3 3 0 3 4 0 3 5 0 3 6 0 3 7 0 4 1 0 4 2 0 4 3 0 4 4 0 4 5 0 4 6 0 4 7 0 5 1 0 5 2 0 5 3 0 5 4 0 5 5 0 5 6 0 5 7 0 6 1 0 6 2 0 6 3 0 6 4 0 6 5 0 6 6 0 6 7 0 7 1 0 7 2 0 7 3 0 7 4 0 7 5 0 7 6 0 7 7 1 1 1 2 1 1 3 1 1 4 1 1 5 1 1 6 1 1 7 1 2 2 1 2 3 1 2 4 1 2 5 1 2 6 1 2 7 1 3 2 1 3 3 1 3 4 1 3 5 1 3 6 1 3 7 1 4 2 1 4 3 1 4 4 1 4 5 1 4 6 1 4 7 1 5 2 1 5 3 1 5 4 1 5 5 1 5 6 1 5 7 1 6 2 1 6 3 1 6 4 1 6 5 1 6 6 1 6 7 1 7 2 1 7 3 1 7 4 1 7 5 1 7 6 1 7 7 2 2 2 3 2 2 4 2 2 5 2 2 6 2 2 7 2 3 3 2 3 4 2 3 5 2 3 6 2 3 7 2 4 3 2 4 4 2 4 5 2 4 6 2 4 7 2 5 3 2 5 4 2 5 5 2 5 6 2 5 7 2 6 3 2 6 4 2 6 5 2 6 6 2 6 7 2 7 3 2 7 4 2 7 5 2 7 6 2 7 7 3 3 3 4 3 3 5 3 3 6 3 3 7 3 4 4 3 4 5 3 4 6 3 4 7 3 5 4 3 5 5 3 5 6 3 5 7 3 6 4 3 6 5 3 6 6 3 6 7 3 7 4 3 7 5 3 7 6 3 7 7 4 4 4 5 4 4 6 4 4 7 4 5 5 4 5 6 4 5 7 4 6 5 4 6 6 4 6 7 4 7 5 4 7 6 4 7 7 5 5 5 6 5 5 7 5 6 6 5 6 7 5 7 6 5 7 7 6 6 6 7 6 7 7 7 (0 0)
υγ. Viva Matala! peace! 🙂
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Ιουνίου, 2015 @ 8:53 μμ
το τελευταιο που ειναι 1 μαλλον εννοειτε 8 για να βγαινει…
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 17 Ιουνίου, 2015 @ 8:54 μμ
7: OK τώρα, είναι κατανοητό. Θα μπορούσε να είναι γραμμένο και καλύτερο αλλά αυτό θα έρθει με το χρόνο. Η ουσία πάντως είναι σωστή.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 9:13 μμ
8: Κι αυτό σωστό φαίνεται!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 9:17 μμ
9: Όντως οι ακολουθίες de Bruijn είναι γενίκευση αυτού που ζητάει το πρόβλημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 9:19 μμ
Αλλαγή στην εκφώνηση τώρα για περισσότερο ενδιαφέρον:
Ας υποθέσουμε τώρα ότι θέλουμε να φτιάξουμε ένα κολιέ με 8 χρώματα όπου θα βλέπουμε ακριβώς μια φορά σε μετάβαση από μια χάντρα στην επόμενη κάθε μη διατεταγμένο ζεύγος χρωμάτων. Τα μη διατεταγμένα ζεύγη από 8 χρώματα είναι όλα τα ζεύγη της μορφής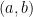
με 
και το πλήθος αυτών είναι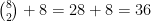 
(o πρώτος προσθετέος μετράει τα ζεύγη με 
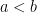και ο δεύτερος αυτά με 
).
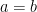Αν π.χ. 1 και 2 είναι δύο από τα χρώματά μας τότε θα δούμε τη μετάβαση 1->2 ή τη μετάβαση 2->1 αλλά όχι και τις δύο. Επίσης θα δούμε τις δύο μεταβάσεις 1->1 και 2->2.
Πώς μπορεί κανείς να φτιάξει ένα τέτοιο κολιέ μήκους 36;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 9:24 μμ
14. Μιχάλη ,είναι δυνατόν κάτι τέτοιο; Ήδη για δύο χρώματα είναι αδύνατον (είτε για κολιέ μήκους 2 ,είτε για κολιέ μήκους 4)
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Ιουνίου, 2015 @ 10:26 μμ
15: Όμως για τρία χρώματα είναι δυνατόν: 112233
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 10:28 μμ
16. Nαι. Χμμ…και για 4 αδύνατον ,και για 5 δυνατόν : 112233442553145
βλέπω ένα pattern να σχηματίζεται (αρτια γιοκ, περιττά ναί!) αλλά είναι αργά για γενικεύσεις…αύριο πάλι! 🙂
υγ. αν και για έναν μηχανικό ,αυτή θα ήταν μια υπερεπαρκέστατη «απόδειξη» για να πει ότι δεν γίνεται για 8… 😆
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Ιουνίου, 2015 @ 11:12 μμ
17: Ναι, σωστά, εμείς εδώ όμως πάντα ρωτάμε το γιατί. Αλλιώς τα μαθηματικά θα ήταν κάτι άλλο. Δε θα υπήρχε λόγος να ψάχνουμε για 350+ χρόνια για την απόδειξη του Τελευταίου Θεωρήματος του Fermat για παράδειγμα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Ιουνίου, 2015 @ 11:16 μμ
18. Ε ναί. Αστείο ήταν ρε συ Μιχάλη ,γιαυτό έβαλα και το απόδειξη σε εισαγωγικά. 🙂 Kαι γώ του «γιατί;» είμαι κατά βάθος, μη νομίζεις!
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Ιουνίου, 2015 @ 11:25 μμ
Όσο γι’αυτόν το Φερμά, καλά να πάθατε οι μαθηματικοί! Αυτή είναι η κατάντια όταν ένα επάγγελμα δεν είναι κατοχυρωμένο και «κλειστό». Μα πού ακούστηκε ένας από τους μεγαλύτερα μαθηματικά μυαλά όλων των εποχών (και λόγιος!) να είναι -άκουσον! άκουσον!- δικηγόρος! 🙂 Μια κόλλα χαρτί για τον κύριο Πετράκη κάποιος ρε παιδιά!
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 17 Ιουνίου, 2015 @ 11:31 μμ
Καλημέρα. Αξίζει να σημειωθεί το εξής συναφές αυτού του προβλήματος, ακολουθία de Bruijn (
) με τη θεωρία γραφημάτων. Πρόκειται για τον $m$-διάστατο υπερκύβο, οποίος έχει σύνολο κομβών όλα τα binary vectors με μήκος 
και ακμές υπάρχουν εκεί που οι κόμβοι διαφέρουν ακριβώς σε μία θέση. Μπορεί να αποδειχθεί επαγωγικά ότι το γράφημα αυτό έχει Hamiltonian Tour για όλα τα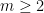 
. Στην ακολουθία de Bruijn θα βλέπαμε δηλαδή μια διάταξη με όλα τα binary vectors με μήκος 
να εμφανίζονται ακριβώς μία φορά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 18 Ιουνίου, 2015 @ 7:38 πμ
ο
-διάστατος υπερκύβος, έχει σύνολο κομβών όλα τα binary vectors με μήκος m και ακμές υπάρχουν εκεί που δύο κόμβοι διαφέρουν ακριβώς σε μία θέση οι συντεταγμένες τους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 18 Ιουνίου, 2015 @ 7:57 πμ
(Συνέχεια στο 17.) Μια απλή απόδειξη αδυναμίας για άρτιο αριθμό χρωμάτων, με βάση στοιχειώδη Θεωρία Γράφων,είναι νομίζω η εξής:
Για να ικανοποιηθεί η συνθήκη του προβλήματος πρέπει αν αντιστοιχίσουμε έναν επίπεδο πλήρη γράφο (αφού πρέπει να υπάρχουν όλες οι δυάδες χρωμάτων) στον οποίον οι κορυφές αντιστοιχούν σε χρώματα (1,2,…,8) και οι ακμές στις ακολουθίες ,αυτός ο γράφος να είναι κύκλωμα Όϋλερ, ή λαϊκά να γράφεται «μονοκονδυλιά». Αφού μόνο τότε η κάθε ακμή διατρέχεται σε έναν κύκλο ΜΙΑ και μόνο φορά (άρα τα ζεύγη είναι διατεταγμένα).
Π.χ για 3 χρώματα, 1,2,3. έχουμε ένα τρίγωνο με ένα βρόχο (loop) σε κάθε κορυφή που αντιστοιχεί στο substring 11, 22, 33 .
Για 4 χρώματα ,ένα τετράγωνο με κορυφές 1,2,3,4 και τις δύο διαγώνιες ΔΕΝ είναι κύκλωμα Euler, αφού ο βαθμός κάθε κορυφής είναι περιττός (=3) .Ως γνωστόν για να είναι Όϋλερ πρεέπει ο βαθμός κάθε κορυφής να είναι άρτιος. Το 5γωνο είναι κύκλωμα Όϋλερ (μια πεντάλφα με το περιβάλον πεντάγωνο ,από κάθε κορυφή-χρώμα φεύγουν 4 ακμές), κ.λ.π. Είναι προφανής η γενίκευση, Για να έχει κάθε ν-γράφος κύκλωμα Εuler με άρτιο βαθμό (degree) πρέπει οι κορυφές να είναι περιττού αριθμού. ΟΕΔ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 9:31 πμ
Ορθή επανάληψη στο 23: «Αφού μόνο τότε η κάθε ακμή διατρέχεται σε έναν κύκλο ΜΙΑ και μόνο φορά (άρα τα ζεύγη είναι ΜΗ διατεταγμένα)»
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 9:33 πμ
πιστευω οτι δε γινεται τετοιο κολιε με 8 χρωματα γιατι αν πουμε οτι οι μεταβασεις ειναι (28)διχρωμες και (8)μονοχρωμες μπαλιτσες τοτε αν τα χρωματα ειναι απο το 1 εως το 8 οι μπαλες θα ειναι: 11, 12, 13, 14, 15, 16, 17, 18, 22, 23, 24, 25, 26, 27, 28, 33, 34 κτλ κτλ και καθε τετοια μπαλα πρεπει μπροστα της να εχει μια μπαλα που θα εχει τον εναν απο τους δυο αριθμους που την αντιπροσωπευουν και πισω της μια αλλη μπαλα που εχει τον αλλο αριθμο…Επισης καθε αριθμος-χρωμα υπαρχει σε 8 μπαλιτσες.. ετσι αν πχ ξεκινησουμε με την 11 πρεπει μεσα στο κολιε να υπαρχουν ολες οι μπαλες, ειδικοτερα καπου θα υπαρχει η 22 που αναγκαστηκα μπροστα της και πισω της εχει μπαλα με τον αριθμο 2. εστω οτι εχει την 23 πισω και 24 μπροστα.. Αρα μενουν 5 μπαλες με το 2.. Επισης καπου μεσα θα υπαρχει και η 25 που ή μπροστα ή πισω εχει την 12 για παραδειγμα.. και ακομα θα ειναι η 26 μαζι με τη 27 πχ.. τοτε θα εχει μεινει μονη της η 28 η οποια πρεπει να εχει μπροστα η πισω μια μπαλα με το 2 που δεν υπαρχει.. αρα δεν γινεται τετοιο κολιε.. δεν ειμαι σιγουρη αν ειναι σωστο…
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 18 Ιουνίου, 2015 @ 10:32 πμ
Eπειδή η τελευταία πρόταση του 23. δεν είναι και πολύ αυστηρή ως προς τη διατύπωση,και ενδεχομένως μπορεί να προκαλέσει σύγχυση,την ξαναγράφω:
Για να έχει κάθε πλήρης γράφος με ν κορυφές (δηλαδή ένα ν-γωνο με όλες τις διαγώνιες) την ιδιότητα που θέλουμε, πρέπει να μπορεί να γραφεί μονοκοντυλιά, δηλαδή να είναι κύκλωμα Euler. Aυτό συμβαίνει μόνο όταν το πολύγωνο έχει περιττό αριθμό κορυφών.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 12:49 μμ
Θα επιχειρήσω μια εναλλακτική απόπειρα απόδειξης, χωρίς γράφους και βαριά μαθηματικά :-).
Καθένα από τα 8 χρώματα του κολιέ, σε κάθε του εμφάνιση (χάντρα του συγκεκριμένου χρώματος), θα πρέπει να έχει και εντελώς διαφορετικό ζευγάρι γειτονικών χρωμάτων και από τις δυο μεριές (αλλιώς θα υπήρχε ζευγάρι χρωμάτων που θα γειτόνευαν περισσότερες από μία φορές). Αυτό συνεπάγεται ότι οι εμφανίσεις κάθε χρώματος θα πρέπει να είναι ακριβώς 8/2 = 4 (αν είναι λιγότερες από 4, θα υπάρχει οπωσδήποτε χρώμα με το οποίο δε γειτονεύει καθόλου, ενώ αν είναι περισσότερες από 4, θα υπάρχει οπωσδήποτε χρώμα με το οποίο γειτονεύει περισσότερες από μία φορές). Με 8 χρώματα όμως και 36 χάντρες, θα υπάρχει σίγουρα χρώμα που εμφανίζεται 5 τουλάχιστον φορές (pigeonhole principle), άρα διπλή εμφάνιση κάποιου ζευγαριού γειτονικών χρωμάτων, πράγμα που δεν θέλουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 18 Ιουνίου, 2015 @ 2:11 μμ
Να το πω καλύτερα: κάθε χρώμα θα πρέπει να εμφανίζεται 5 φορές, αφού τη φορά που μια χάντρα ενός χρώματος Χ1 θα γειτονεύει με χάντρα ιδίου χρώματος σε μια διάταξη- Χ1-Χ1-, αρκεί οι χάντρες αριστερά της αριστερής και δεξιά της δεξιάς να είναι διαφορετικών χρωμάτων. Έτσι, με μια τέτοια διπλή εμφάνισή του το χρώμα Χ1 καλύπτει άμεση γειτνίαση με 2 διαφορετικά χρώματα συν 1 τον εαυτό του (π.χ. -Χ2-Χ1-Χ1-Χ3-) και μένει να καλυφθεί η γειτνίαση του Χ1 με 5 ακόμα διαφορετικά χρώματα (Χ4, Χ5, Χ6, Χ7, Χ8), η οποία απαιτεί περισσότερες από 2 ακόμα εμφανίσεις χάντρας Χ1. Άρα τουλάχιστον 2+3=5 εμφανίσεις. Για 8 χρώματα θα χρειαζόμασταν 8*5=40 τουλάχιστον χάντρες και σίγουρα θα είχαμε διπλές εμφανίσεις ζευγαριών χρωμάτων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 18 Ιουνίου, 2015 @ 2:45 μμ
26 και προηγούμενα σχόλια: Είναι βέβαια στη σωστή κατεύθυνση το επιχείρημα αλλά δεν είναι καθόλου σαφές το ποιος είναι ο γράφος. Π.χ. στην περίπτωση 4 χρωμάτων λες ότι έχεις βαθμό 3 σε κάθε κορυφή, άρα δε βάζεις loop σε κάθε κορυφή ενώ είχες βάλει τέτοιο στην περίπτωση του τριγώνου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 4:26 μμ
25: Το διάβασα και τώρα χρειάζομαι παυσίπονο. Δεν καταλαβαίνω τίποτα. Γιατί οι μπάλες σου έχουν ονόματα από δύο χρώματα π.χ.; Τι αντιπροσωπεύουν αυτά τα ονόματα;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 4:28 μμ
28 & 27: Πάρα πολύ καλό!
Γενικεύεται και για κάθε άρτιο;
Τι γίνεται με περιττό πλήθος χρωμάτων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 4:36 μμ
Ευχαριστώ! Νομίζω πως γενικεύονται και τα δυο, αλλά το περιθώριό μου (χρόνου) είναι πολύ μικρό (αυτό ήταν ένα ακόμα μνημόσυνο στο Φερμά 🙂 ) για να παραθέσω άμεσα την απόδειξη. Θα το κάνω ίσως αργότερα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 18 Ιουνίου, 2015 @ 4:48 μμ
οι μπαλες ειναι διχρωμες και παριστανουν τη μεταβαση απο το ενα χρωμα στο αλλο γι αυτο τις ονομαζουμε με δυο χρωματα.. επισης αυτες θα ειναι ολες οι δυνατες μεταβασεις γιατι αν πχ εχουμε την μπαλα 12 (με χρωματα 1 και 2) τη βλεπουμε ειτε σαν μεταβαση απο το 1 στο 2 ειτε απο το 2 στο 1… αρα για το κολιε που ζητατε πρεπει να χρησιμοποιηθουν ολες απο μια φορα που δεν γινεται (οπως ειπα για παραδειγμα με αυτες που περιεχουν το χρωμα 2)…
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 18 Ιουνίου, 2015 @ 5:07 μμ
25: Γιατί δε μπορείς να έχεις 4 μπάλες στη σειρά που να περιέχουν όλες το 2; Αυτό θέλει αιτιολόγηση για να δουλεύει το επιχείρημά σου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 6:31 μμ
γιατι καθε μπαλα πρεπει να ειναι αναμεσα σε δυο μπαλες που περιεχουν η καθεμια τον εναν απο τους δυο τις αριθμους ετσι πχ αν εχουμε την 24 (παριστανει τη μεταβαση απο το χρωμα 2 στο 4 (ή απο το 4 στο 2 αλλα δεν αλλαζει σχεδον τιποτα οποτε θεωρουμε το πρωτο) οποτε πισω πρεπει να ειναι μια που παριστανει μεταβαση απο το χρωμα α στο 2 και μπροστα μια που παριστανει τη μεταβαση απο το 4 στο β) πρεπει να ειναι αναμεσα σε μια που εχει το 2 και μια που εχει το 4 αρα μπορει να ειναι ετσι και για να ειναι ειναι τρεις μπαλες στη σειρα που εχουν το 2 θα πρεπει να ειναι καπως ετσι: 23-24-42 γιατι πρεπει να υπαρχει στη μια υποχρεωτικα το 4..ομως η 24 ειναι ιδια με την 42 αρα αυτο δεν γινεται.. στην περιπτωση που η μεσαια ειναι η 22 ειναι η μονη περιπτωση που μπορουν να μπαινουν τρεις μπαλες με το 2 στη σειρα αλλα δεν μπορει να μπει τεταρτη για τον ιδιο λογο με πριν… προσπαθησα οσο καλυτερα μπορουσα πιστευω.. γενικα δεν το χω με την αιτιολογηση πολυ..
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 18 Ιουνίου, 2015 @ 6:56 μμ
35: Αποδεκτή η αιτιολόγηση. Όσο γράφεις τόσο καλύτερα θα τα γράφεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 6:58 μμ
το «αρα μπορει να ειναι ετσι» στην εκτη σειρα μπηκε κατα λαθος..
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 18 Ιουνίου, 2015 @ 7:00 μμ
χαχα ειναι λιγο δυσκολο ομως… θα προσπαθησω παντως να βελτιωθω
Μου αρέσει!Μου αρέσει!
Σχόλιο από valeria fr — 18 Ιουνίου, 2015 @ 7:01 μμ
Θα προσπαθήσω να απαντήσω στο ερώτημα της γενίκευσης:
Αν έχουμε ν διαφορετικά χρώματα, τότε οι απαραίτητες μεταβάσεις είναι ν(ν-1)/2 + ν = ν(ν+1)/2 και τόσες ακριβώς πρέπει να βγαίνουν και οι χάντρες. Οι ελάχιστες εμφανίσεις (χάντρες) ενός χρώματος για να γειτονεύει με όλους τους επιθυμητούς τρόπους με τα άλλα χρώματα και τον εαυτό του είναι το ταβάνι (ο αμέσως μεγαλύτερος ή ίσος ακέραιος) του (ν+1)/2.
Όταν ο ν είναι άρτιος, όπως στην περίπτωση ν=8 που είδαμε, τότε ο (ν+1)/2 δεν βγαίνει ακέραιος, οπότε καθένα από τα ν χρώματα πρέπει να εμφανίζεται (ν+2)/2 φορές, άρα ο συνολικός αριθμός χαντρών είναι τουλάχιστον ν(ν+2)/2 και είναι μεγαλύτερος του ν(ν+1)/2 που είναι ο επιθυμητός αριθμός μεταβάσεων. Στην περίπτωση αυτή, έχουμε υπέρβαση αριθμού χαντρών και θα υπάρξουν υποχρεωτικά διπλές μεταβάσεις μεταξύ χρωμάτων.
Όταν ο ν είναι περιττός, τότε ο (ν+1)/2 είναι ακέραιος, οπότε κάθε χρώμα μπορεί να εμφανίζεται ακριβώς (ν+1)/2 φορές και ο συνολικός αριθμός χαντρών να είναι ακριβώς ν(ν+1)/2, όσες δηλαδή και οι απαιτούμενες μεταβάσεις. Το ότι δεν έχουμε όμως πρόβλημα με την αριθμητική, στην περίπτωση περιττού ν, δεν απαντάει πλήρως το ερώτημα, αν δεν παραθέσει κανείς και τον τρόπο που χτίζει το κολιέ. Αυτό, ομολογώ, δεν το έχω ελέγξει εξονυχιστικά, στη γενική πάντα περίπτωση, αλλά θα το πιστέψω σίγουρα όταν/αν το δω.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 18 Ιουνίου, 2015 @ 7:40 μμ
39: Πολύ ωραία.
Για περιττό αριθμό χρωμάτων πώς;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 7:42 μμ
29. Γιατί δεν είναι σαφές; Ένα loop σε κάθε κορυφή/χρώμα/αριθμός υπάρχει πάντα. Εξυπακούεται αυτό, για να ορίσει το substring xx (11,22, 33, κ.λ.π) Το loop βρόχο δεν το μετράω στο βαθμό της κορυφής ή μπορεί κάποιος να το μετρήσει ως 2, αφού είναι ακμή αυτοεπιστεφόμενη. Όσους βρόχους θέλω κάνω σε ένα γράφημα που με ενδιαφέρει η Οϋλερικότητά του. Δεν αλλάζει κάτι. Όσο για την ιδέα των γράφων δεν υπάρχει απλούστερη. Κάθε κορυφή αντιπροσωπεύει ένα χρώμα και κάθε ακμή τη συγκεκριμένη μετάβαση απο κορυφή αρχής σε κορυφή τέλους. Αν το κύκλωμα -ξεκινώντας από μία οποιαδήποτε κορυφή και καταλήγοντας σε αυτή- είναι Euler ,η συνθήκη του προβλήματος πληρούται. Αφού έχω περάσει από όλες τις ακμές ΜΙΑ μόνο φορά (δηλαδή η κάθε δυνατή δυάδα εμφανίζεται στο κολιέ μία φορά. Μόνο η x1x2 ή η x2x1 αλλά όχι και οι δύο)
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 8:30 μμ
41: Δεν ήταν σαφές. Τώρα που λες: «Ένα loop σε κάθε κορυφή/χρώμα/αριθμός υπάρχει πάντα. … Το loop βρόχο δεν το μετράω στο βαθμό της κορυφής ή μπορεί κάποιος να το μετρήσει ως 2 » είναι πλέον σαφές.
Έχεις ένα γράφημα λοιπόν με μια κορυφή για κάθε χρώμα και μια ακμή από κάθε κορυφή προς κάθε άλλη και προς τον εαυτό της. Αν κανείς πάρει ένα κύκλωμα Euler στο γράφημα αυτό (ένα μονοπάτι δηλ. που ξεκινά από κάποια κορυφή και επιστρέφει σε αυτήν και περνάει από κάθε ακμή ακριβώς μια φορά) τότε μπορεί να κατασκευάσει ένα κολιέ απλά καταγράφοντας τα χρώματα των κορυφών που επισκέπτεται. Το κολιέ αυτό θα έχει την ιδιότητα που θέλουμε επειδή κάθε ακμή έχει διανυθεί ακριβώς μια φορά και επειδή οι ακμές του γραφήματος είναι σε 1-1 αντιστοιχία με τις δυνατές μεταβάσεις. Εύκολα βλέπει κανείς ότι και κάθε κολιέ με την ιδιότητα που ζητάμε ορίζει ένα κύκλωμα Euler στο γράφημα αυτό. Άρα το κολιέ υπάρχει αν και μόνο αν υπάρχει κύκλωμα Euler στο γράφημα αυτό.
Πότε ένα γράφημα έχει κύκλωμα Euler;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Ιουνίου, 2015 @ 8:38 μμ
Yπάρχουν 3 θεωρήματα του ίδιου του μπάρμπα Όϋλερ :
1ο
Αν ένα γράφημα γενικά (ή «γράφος» που προτιμώ σαν όρο,για να μην συγχέεται με το γράφημα συναρτήσεων),έχει κορυφές περιττού βαθμού (δηλαδή φεύγει ή έρχεται ανάλογα με τη θεωρούμενη φορά διαγραφής, περιττός αριθμός ακμών στον κόμβο) τότε δεν μπορεί να έχει κύκλωμα Όϋλερ.
και
Αν ένας γράφος είναι συνεκτικός/πλήρης (connected)[δηλαδή κάθε κορυφή του συνδέεται με ακμές με όλες τις υπόλοιπες] και ΚΑΘΕ κόμβος/κορυφή είναι άρτιου βαθμού, τότε έχει ΤΟΥΛΑΧΙΣΤΟΝ ΕΝΑ (συνήθως περισσότερα) κυκλώματα Όϋλερ.
Το 2ο θεώρημα μιλάει για τα Όϋλερ paths ,ας το αφήσουμε.
Το 3ο θεώρημα του γκαϊδού λέει:
Tο άθροισμα των βαθμών όλων των κόμβων ενός γραφήματος είναι άρτιος αριθμός (2 φορές ο αριθμός των ακμών).
Σε κάθε γράφο,ο αριθμός των κόμβων περιττού βαθμού πρέπει να είναι άρτιος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 8:59 μμ
Συνάγεται λοιπόν (ελπίζω…πιά!) ότι κανένα πολύγωνο «πλήρες» (με όλες τις ακμές του και τις διαγώνιές του γραμμένες) με ν άρτιος κορυφές δεν μπορεί να είναι κύκλωμα Όϋλερ ,αφού οι ακμές από κάθε κορυφή προς τις υπόλοιπες είναι όλες περιττοί αριθμοί.
Μου αρέσει!Μου αρέσει!
Σχόλιο από George Rizopulos — 18 Ιουνίου, 2015 @ 9:02 μμ
42, 43: Ένας άλλος χαρακτηρισμός είναι να μπορούν να ομαδοποιηθούν οι ακμές σε ξἐνους ανά δύο και εν γένη κύκλους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 18 Ιουνίου, 2015 @ 9:24 μμ
Ένα συνεκτικό γράφημα λοιπόν έχει κύκλωμα Euler αν και μόνο αν κάθε κορυφή του έχει άρτιο βαθμό (δηλ. πλήθος ακμών που φεύγουν από αυτή).
Γιατί; Είναι δύσκολο αυτό;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 10:15 πμ
Έστω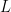
, κλειστό μονοπάτι Euler που καλύπτει όλες τις κόρυφές στο γράφο 
, ο οποίος υποθέτουμε είναι πεπερασμένος. Θα αποδείξουμε ότι κάθε κορυφή έχει βαθμό 2. Απόδειξη: Η παρουσία κάθε κορυφής στο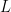 
, του γράφου συνεισφέρει 2 στο βαθμό αυτής της κορυφής, αφού το μονοπάτι, εισέρχεται στην κορυφή και εξέρχεται. Αφού κάθε ακμή του γράφου, εμφανίζεται ακριβώς μία φορά στο 
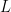, κάθε κορυφή έχει άρτιο βαθμό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 1:08 μμ
Τώρα θα αποδείξουμε ότι αν κάθε κορυφή έχει άρτιο βαθμό, οι ακμές ομαδοποιούνται σε κύκλους. Αφού ο
είναι συνδεδεμένος, στην κορυφή με τον ελάχιστο βαθμό (στη βιβλιογραφία ο βαθμός αυτής συμβολίζεται με 
), ισχύει 
. Αυτό σημαίνει όμως ότι στον 
υπάρχει κύκλος, έστω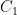 
. Αυτό φαίνεται αν αναλογιστούμε κάθε περίπατο ξεκινώντας από μια κορυφή. Αφού 
, κάθε κορυφή που φθάνουμε μπορούμε να αφήσουμε (να φύγουμε από αυτήν). Μιας και ο γράφος είναι πεπερασμένος πρέπει ο κύκλος να κλείσει. Τώρα αν αποκόψουμε τις ακμές του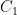 
από τον γράφο μένουμε με ένα νέο γράφο (έστω 
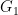), με όλες τις κορυφές αυτού να έχουν άρτιο βαθμό. Συνεχίζουμε κάνοντας αυτή την διαδικασία ξανά και ξανά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 1:36 μμ
Τώρα θα αποδείξουμε ότι αν οι ακμές ομαδοποιούνται σε κύκλους τότε ο γράφος έχει κύκλωμα Euler. Aν ο γράφος είναι ένας κύκλος από μόνος του έστω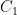
, αυτό είναι προφανές. Έστω λοιπόν ότι υπάρχει ακόμη ένας κύκλος 
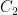, στο γράφο που μοιράζεται ένα κόμβο 
με τον $C_1$. Ο περίπατος που ξεκινάει από τον κόμβο 
και καλύπτει όλες τις ακμές των δύο κύκλων είναι κλειστό μονοπάτι Euler, χωρίς απαραίτητα να καλύπτει όλες τις κορυφές του 
αφού πιθανόν ο γράφος να έχει και άλλους κύκλους. Συνεχίζουμε την διαδικασία αυτή προσθέτοντας ένα ακόμη κύκλο στο 
έτσι ώστε να έχουν κοινό κόμβο. Υφίσταται κύκλωμα και στον νέο αυτό γράφο. Με επαγωγή, προσθέτοντας κύκλους εκεί που πρέπει, έχουμε κύκλωμα Euler στον αρχικό μας γράφο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 4:01 μμ
Θα αποδείξουμε ότι κάθε κορυφή έχει βαθμό άρτιο εννοούσα στο 47. Συνοπτικά έχουμε 3 προτάσεις: (i) Κύκλωμα Euler υπάρχει στον γράφο. (ii) Κάθε κορυφή έχει άρτιο βαθμό (iii) Ομαδοποίηση σε κύκλους. Χρησιμοποιώντας το (i) αποδείξαμε το (ii). Μετά χρησιμοποιώντας το (ii) αποδείξαμε το (iii) και τέλος από το (iii) το (i).
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 4:45 μμ
47: Σωστό. Αυτό αποδεικνύει ότι το να έχουμε παντού άρτιο βαθμό είναι αναγκαίο για να υπάρχει κύκλωμα Euler.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 5:05 μμ
48-50: Πού βρίσκουμε το δεύτερο κύκλο; Καλά τον πρώτο τον καταλαβαίνω: ξεκινάμε από μια κορυφή και κινούμαστε προς οποιαδήποτε γειτονική πάντα πάνω σε μη χρησιμοποιημένη ακμή. Όταν πλέον δε μπορούμε να το κάνουμε αυτό τότε βρισκόμαστε σε μια κορυφή με καμιά αχρησιμοποίητη ακμή. Αυτή είναι αναγκαστικά η κορυφή από την οποία ξεκινήσαμε αφού, λόγω του άρτιου βαθμού, όσες φορές μπαίνουμε σε μια κορυφή τόσες φορές βγαίνουμε επίσης.
Έτσι προκύπτει ένας κύκλος που όμως μπορεί να μη καλύπτει τα πάντα.
Αφαιρώντας τον μένουν όλες οι κορυφές με άρτιο βαθμό. Αυτό είναι φανερό. Δεν είναι όμως πλέον το γράφημα κατ’ ανάγκη συνεκτικό. Πώς προκύπτουν οι άλλοι κύκλοι; Μπορείς να μας το ξεκαθαρίσεις;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 5:15 μμ
Αφού αφαιρέσουμε τις ακμές του πρώτου κύκλου από τον
, έχουμε ένα νέο γράφο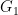 
του οποίου οι κορυφές έχουν άρτιο βαθμό όπως είπαμε. Οι κορυφές όμως του 
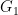είναι όλες συνδεδεμένες μεταξύ τους. Από μία συνδεδεμένη συνιστώσα λοιπόν βρίσκουμε τον νέο κύκλο με ακριβώς τον ίδιο τρόπο. Ο βαθμός των κορυφών που χάνονται σε κάθε αποκοπή κύκλου είναι 2.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 6:24 μμ
53: Μετά την αφαίρεση του πρώτου κύκλου το νέο γράφημα μπορεί να έχει πολλές συνεκτικές συνιστώσες. Δεν είναι όλες οι κορυφές του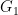
(όπως το ονομάζεις) συνδεδεμένες μεταξύ τους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 6:27 μμ
Μπορεί να μένουν κάποιοι κόμβοι απομονωμένοι δηλαδή μετά από κάποια αποκοπή κύκλου; Δεν το βλέπω πραγματικά. Αφού οι κόμβοι που χάνονται κάθε φορά έχουν βαθμό 2 ο κάθε ένας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 6:52 μμ
Φυσικά και μπορεί να αποσυνδεθεί το γράφημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Ιουνίου, 2015 @ 6:53 μμ
Έχετε δίκαιο. Μπορεί να αποσυνδεθεί αν αποκοπεί κύκλος που συνδέει δύο ή και περισσότερες συνεκτικές συνιστώσες. Τότε βρίσκουμε τον νέο κύκλο σε κάποια από αυτές τις συνδεδεμένες.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 7:12 μμ
Στο τέλος μένουν απομονωμένοι κόμβοι και οι κύκλοι που αποκόπηκαν.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 7:16 μμ
Λάθος αυτό. Ο επόμενος κύκλος βρίσκετε σε δύο απομονωμένες μεταξύ τους συνδεδεμένες συνιστώσες.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 7:23 μμ
57,58,59 λάθος. Θα το ξανασκεφτώ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 7:29 μμ
Το λοιπόν. Πράγματι ο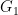
δεν είναι κατανάγκην συνδεδεμένος. Αυτό όμως δεν παίζει κανένα ρόλο στην ύπαρξη νέου κύκλου. Οι κύκλοι υπάρχουν στις συνδεδεμένες συνιστώσες φυσικά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 8:08 μμ
Έστω κόμβοι 1,2,3,4,5,6,7. 1-2-3 τρίγωνο, 3,4,5 τρίγωνο, 5,6,7 τρίγωνο. Αποκόπτουμε το τρίγωνο 3,4,5. Ο γράφος που απομένει δεν είναι συνδεδεμένος. Υπάρχουν όμως οι 2 κύκλοι, τα δύο τρίγωνα που δεν είναι συνδεδεμένα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 8:13 μμ
62, συνέχεια. Μετά την αποκοπή του τριγώνου 3-4-5, ο κόμβος 4 μένει απομονωμένος από το υπόλοιπο γράφημα. Έτσι θα συμβαίνει λοιπόν. Στο τέλος θα έχουμε την ένωση κάποιων κύκλων (που είναι αυτοί που αποκόπηκαν) και κάποιους απομονωμένους κόμβους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 8:27 μμ
Στο τέλος μόνο απομονωμένοι κόμβοι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Κωνσταντίνος Κουρουζίδης — 19 Ιουνίου, 2015 @ 8:34 μμ