Υποθέστε ότι θέλετε να δηλητηριάσετε την πεθερά σας. Σας επισκέπτεται για τσάι και επιλέγει 
κουλουράκια στη τύχη από ένα μπώλ που περιέχει 
κουλουράκια, όπου 
.
κουλουράκια στη τύχη από ένα μπώλ που περιέχει κουλουράκια, όπου .Έχετε στην κατοχή σας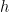 
γραμμάρια αρσενικό, όπου 
και η θανατηφόρα δόση είναι το 1 γραμμάριο. Δυστυχώς δε μπορείτε να βάλετε το δηλητήριο στο τσάι της. Θα πρέπει να το βάλετε στα κουλουράκια. Πώς πρέπει να κατανείμετε το δηλητήριο στα κουλουράκια ώστε να μεγιστοποιήσετε την πιθανότητα να την «ξεκάνετε» ;
γραμμάρια αρσενικό, όπου και η θανατηφόρα δόση είναι το 1 γραμμάριο. Δυστυχώς δε μπορείτε να βάλετε το δηλητήριο στο τσάι της. Θα πρέπει να το βάλετε στα κουλουράκια. Πώς πρέπει να κατανείμετε το δηλητήριο στα κουλουράκια ώστε να μεγιστοποιήσετε την πιθανότητα να την «ξεκάνετε» ;Πρόβλημα από τον Χρήστο Πελέκη.
Προβλήματα Μαθηματικών 
Πολύ ενδιαφέρον πρόβλημα!
Θα ήθελα κάποιες διευκρινίσεις, αν είναι διαθέσιμες.
1ον. Η πεθερά τρώει υποχρεωτικά φαντάζομαι όλα όσα επιλέξει (;)
2ον. Ζητείται μια «ενιαία» ας την πούμε κατανομή, ανεξαρτήτως S , ή μπορούμε να θεωρήσουμε «περιπτώσεις» (πράγμα που κάποιες πρώτες σκέψεις μου με οδηγούν στο συμπέρασμα ότι αυτή είναι η ενδεδειγμένη στρατηγική) . Δηλαδή, διαφορετική αντιμετώπιση για μικρά n και διαφορετική για μεγάλα. Αντιλαμβάνομαι βέβαια, ότι αυτη η ερώτηση συνιστά -τρόπον τινά- προσπάθεια υποκλοπής hint ,οπότε δεν θα σας παρεξηγήσω αν δεν απαντήσετε. 🙂
3oν. το διάστημα του h είναι σίγουρα ημιανοικτό; Μήπως είναι <ή ίσον του 2; Ρωτώ ,για να αποκλειστεί το ενδεχόμενο τυπογραφικού λάθους.
Ευχαριστώ εκ των προτέρων για τυχόν διαθέσιμες απαντήσεις!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 1 Νοεμβρίου, 2013 @ 4:47 μμ
1. Ναι, τα τρώει όλα.
2. Η στρατηγική σου μπορεί να εξαρτάται από το n και το s. Αν δεν εξαρτάται κι από το s ακόμη καλύτερα.
3. Το διάστημα για το h είναι σίγουρα ημιανοιχτό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 1 Νοεμβρίου, 2013 @ 4:59 μμ
Δίνω περιληπτικά την απάντηση που νομίζω σωστή και, αν δεν υπάρχει λάθος ουσίας, μπορώ να στείλω και την ανάλυσή μου.
Καταρχήν, νομίζω ότι θα πρέπει να θεωρήσουμε ότι s >= 1.
Οι αντίπαλες στρατηγικές είναι κατά βάση οι εξής δύο:
α) Ρίχνουμε μια θανατηφόρα δόση του 1 γρ. σε ένα μόνο κουλουράκι και έχουμε πιθανότητα s/n να είναι αυτό ένα από τα s κουλουράκια που θα διαλέξει η πεθερά.
β) Μοιράζουμε ισόποσα το δηλητήριο σε ένα μεγαλύτερο αριθμό από κουλουράκια. Στην περίπτωση αυτή όμως, αν δηλητηριάσουμε όλα τα κουλουράκια ή αν δηλητηριάσουμε τόσα που η δόση σε κάθε δηλητηριασμένο κουλουράκι είναι μικρότερη από 1/s, τότε με τα s κουλουράκια που θα φάει η πεθερά, δε θα βγει θανατηφόρα δόση, τουλάχιστον 1 γρ., με δεδομένα h<2 και s<=n/2. Κατά μέγιστο (για s=n/2 και h οριακά υπολειπόμενο από τα 2 γρ.) μπορούμε να δηλητηριάσουμε αποτελεσματικά μέχρι n-1 το πολύ κουλουράκια (αφού αν δηλητηριάζαμε n κουλουράκια, η δόση δηλητηρίου ανά κουλουράκι θα ήταν h/n < 2/2s = 1/s). Αλλά για οποιονδήποτε αριθμό από 2 μέχρι n-1 δηλητηριασμένα κουλουράκια, η πιθανότητα ‘επιτυχίας’, όπως υπολογίζεται με απλή συνδυαστική ανάλυση, ακόμα κι όταν δεν είναι μηδενική, είναι μικρότερη (ή οριακά ίση) από s/n.
Επομένως, ακολουθούμε τη στρατηγική α (που επί πλέον ξοδεύει μόνο το 1 γρ. από το δηλητήριο που διαθέτουμε και εξοικονομεί το τυχόν υπόλοιπο για κάποια άλλη θεάρεστη χρήση).
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 8 Νοεμβρίου, 2013 @ 10:02 μμ
Το (α) του άνω σχολίου είναι σαφές. Μπορείς να μας εξηγήσεις λίγο πιο αναλυτικά το (β) ;
Επιχειρηματολογείς ότι η πιθανότητα «να μοιράσουμε ισόποσα το δηλητήριο σε x>1 κουλουράκια»
είναι μικρότερη ή ίση της πιθανότητας «να βάλουμε 1γρ σε ένα κουλουράκι».
Μπορεί όμως να υπάρχει μια κατανομή δηλητηρίου που να μην έχει ισόποσες δόσεις και να
έχει καλύτερη πιθανότητα να ξεκάνει την πεθερά..
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 9 Νοεμβρίου, 2013 @ 4:42 μμ
Ευχαριστώ καταρχάς για την προσοχή και το σχόλιό σας.
Σχετικά με το ερώτημα μήπως με κάποια στρατηγική ανισοκατανομής του δηλητηρίου σε πολλά κουλουράκια θα μπορούσε να υπάρξει βέλτιστο αποτέλεσμα, η απάντηση είναι νομίζω αρνητική. Φυσικά, δεν είμαι σε θέση να το αποδείξω, νομίζω όμως ότι δεν υπάρχει μέχρι στιγμής και το αντιπαράδειγμα -:).
Αν λοιπόν ισχύει η εικασία Kikuta-Ruckle, η οποία στα εδώ συμφραζόμενα νομίζω μας επιτρέπει να θεωρήσουμε ότι η βέλτιστη στρατηγική αντιστοιχεί σε ένα είδος ισοκατανομής του δηλητηρίου σε κάποιον αριθμό κουλουριών, η ανάλυση / σύγκριση περιορίζεται μεταξύ των εναλλακτικών στρατηγικών ισοκατανομής σε ένα ή περισσότερα κουλουράκια.
Αφού η πεθερά διαλέγει στην τύχη και τρώει s κουλουράκια, καταλληλότερη στρατηγική έναντι των άλλων είναι εκείνη που μεγιστοποιεί το πλήθος των συνδυασμών από s κουλουράκια, στα οποία να περιέχεται αθροιστικά τουλάχιστον 1 γρ. δηλητήριο.
Έστω δ (1<=δ= 1 γρ.) και κατά συνέπεια ο αριθμός δ δεν πρέπει να υπερβαίνει ένα μέγιστο που προσδιορίζεται ως max(δ)=h/(1/s)=h*s και, δεδομένου ότι δ ακέραιος, max(δ)=floor(h*s).
Κρίσιμο μέγεθος για τον υπολογισμό του πλήθους των θανατηφόρων συνδυασμών (και κατ’ επέκταση της πιθανότητας επιτυχίας κάθε στρατηγικής) είναι η ελάχιστη απαιτούμενη κατανάλωση από την πεθερά δηλητηριασμένων κουλουριών για να προκύψει θανατηφόρα δόση >= 1 γρ. Ο ελάχιστος αυτός αριθμός κουλουριών, έστω ε, είναι συνάρτηση του δ και του h και υπολογίζεται σε ε= 1/(h/δ)=δ/h και, δεδομένου ότι ε ακέραιος, ε=ceiling(δ/h).
Για να είναι, επομένως, ένας συνδυασμός από s κουλουράκια θανατηφόρος, θα πρέπει να περιλαμβάνει από ε έως min(s,δ) δηλητηριασμένα κουλουράκια και τα υπόλοιπα, αντιστοίχως από s-ε έως s-min(s,δ), μη δηλητηριασμένα.
Το πλήθος θανατηφόρων συνδυασμών υπολογίζεται από το άθροισμα των γινομένων όλων των πιο πάνω επί μέρους συνδυασμών.
Το συνολικό πλήθος των θανατηφόρων και μη συνδυασμών s από n κουρουράκια υπολογίζεται ως C(n,s)=n!/[(s!(n-s)!].
Το πηλίκο θανατηφόρων προς συνολικούς συνδυασμούς μας δίνει το μέτρο της πιθανότητας επιτυχίας κάθε στρατηγικής, όπως προσδιορίζεται με παραμέτρους τις τιμές των n, s, h και δ εντός των ορίων που δίνονται ή προκύπτουν από την ανάλυση.
Από τη διερεύνηση των εναλλακτικών σεναρίων τιμών των υπόψη παραμέτρων, με τη συνδρομή και υπολογιστικού βοηθήματος excel, προκύπτει ότι η στρατηγική της ισόποσης κατανομής σε πολλά κουλουράκια μειονεκτεί συστηματικά έναντι της στρατηγικής της τοποθέτησης μιας θανατηφόρας δόσης 1 γρ. σε ένα μόνο κουλουράκι.
Οι μοναδικές περιπτώσεις που οι δύο στρατηγικές καταλήγουν σε ισοδύναμα αποτελέσματα είναι όταν:
s=n/2 (n άρτιος)
h: εγγύτατα στο όριο των 2 γρ.
δ περιττός
Σε τέτοιες περιπτώσεις η απόδοση και των δύο στρατηγικών είναι ½ που είναι και το μέγιστο εφικτό, με τους δεδομένους περιορισμούς.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 13 Νοεμβρίου, 2013 @ 2:28 πμ
Το ξαναστέλνω διότι κάποια σημεία δεν ήρθαν σωστά στο προηγούμενο.
Ευχαριστώ καταρχάς για την προσοχή και το σχόλιό σας.
Σχετικά με το ερώτημα μήπως με κάποια στρατηγική ανισοκατανομής του δηλητηρίου σε πολλά κουλουράκια θα μπορούσε να υπάρξει βέλτιστο αποτέλεσμα, η απάντηση είναι νομίζω αρνητική. Φυσικά, δεν είμαι σε θέση να το αποδείξω, νομίζω όμως ότι δεν υπάρχει μέχρι στιγμής και το αντιπαράδειγμα .
Αν λοιπόν ισχύει η εικασία Kikuta-Ruckle, η οποία στα εδώ συμφραζόμενα νομίζω μας επιτρέπει να θεωρήσουμε ότι η βέλτιστη στρατηγική αντιστοιχεί σε ένα είδος ισοκατανομής του δηλητηρίου σε κάποιον αριθμό κουλουριών, η ανάλυση / σύγκριση περιορίζεται μεταξύ των εναλλακτικών στρατηγικών ισοκατανομής σε ένα ή περισσότερα κουλουράκια.
Αφού η πεθερά διαλέγει στην τύχη και τρώει s κουλουράκια, καταλληλότερη στρατηγική έναντι των άλλων είναι εκείνη που μεγιστοποιεί το πλήθος των συνδυασμών από s κουλουράκια, στα οποία να περιέχεται αθροιστικά τουλάχιστον 1 γρ. δηλητήριο.
Έστω δ (1<=δ= 1 γρ.) και κατά συνέπεια ο αριθμός δ δεν πρέπει να υπερβαίνει ένα μέγιστο που προσδιορίζεται ως max(δ)=h/(1/s)=h*s και, δεδομένου ότι δ ακέραιος, max(δ)=floor(h*s).
Κρίσιμο μέγεθος για τον υπολογισμό του πλήθους των θανατηφόρων συνδυασμών (και κατ’ επέκταση της πιθανότητας επιτυχίας κάθε στρατηγικής) είναι η ελάχιστη απαιτούμενη κατανάλωση από την πεθερά δηλητηριασμένων κουλουριών για να προκύψει θανατηφόρα δόση >= 1 γρ. Ο ελάχιστος αυτός αριθμός κουλουριών, έστω ε, είναι συνάρτηση του δ και του h και υπολογίζεται σε ε= 1/(h/δ)=δ/h και, δεδομένου ότι ε ακέραιος, ε=ceiling(δ/h).
Για να είναι, επομένως, ένας συνδυασμός από s κουλουράκια θανατηφόρος, θα πρέπει να περιλαμβάνει από ε έως min(s,δ) δηλητηριασμένα κουλουράκια και τα υπόλοιπα, αντιστοίχως από s-ε έως s-min(s,δ), μη δηλητηριασμένα.
Το πλήθος θανατηφόρων συνδυασμών υπολογίζεται από το άθροισμα των γινομένων όλων των πιο πάνω επί μέρους συνδυασμών.
Το συνολικό πλήθος των θανατηφόρων και μη συνδυασμών s από n κουρουράκια υπολογίζεται ως C(n,s)=n!/[(s!(n-s)!].
Το πηλίκο θανατηφόρων προς συνολικούς συνδυασμούς μας δίνει το μέτρο της πιθανότητας επιτυχίας κάθε στρατηγικής, όπως προσδιορίζεται με παραμέτρους τις τιμές των n, s, h και δ εντός των ορίων που δίνονται ή προκύπτουν από την ανάλυση.
Από τη διερεύνηση των εναλλακτικών σεναρίων τιμών των υπόψη παραμέτρων, με τη συνδρομή και υπολογιστικού βοηθήματος excel, προκύπτει ότι η στρατηγική της ισόποσης κατανομής σε πολλά κουλουράκια μειονεκτεί συστηματικά έναντι της στρατηγικής της τοποθέτησης μιας θανατηφόρας δόσης 1 γρ. σε ένα μόνο κουλουράκι.
Οι μοναδικές περιπτώσεις που οι δύο στρατηγικές καταλήγουν σε ισοδύναμα αποτελέσματα είναι όταν:
s=n/2 (n άρτιος)
h: εγγύτατα στο όριο των 2 γρ.
δ περιττός
Σε τέτοιες περιπτώσεις η απόδοση και των δύο στρατηγικών είναι ½ που είναι και το μέγιστο εφικτό, με τους δεδομένους περιορισμούς.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 13 Νοεμβρίου, 2013 @ 2:34 πμ
Ούτε στη δεύτερη, οπότε στέλνω το κομμάτι που μάσησε.
…………………………………………………….
Έστω δ (1 <= δ= 1 γρ.) και κατά συνέπεια ο αριθμός δ δεν πρέπει να υπερβαίνει ένα μέγιστο που προσδιορίζεται ως max(δ)=h/(1/s)=h*s και, δεδομένου ότι δ ακέραιος, max(δ)=floor(h*s).
………………………………………….
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 13 Νοεμβρίου, 2013 @ 2:37 πμ
Διευκρινίζω απλώς ότι δ ονομάζω τον αριθμό των δηλητηριασμένων κουλουριών που περιέχουν τουλάχιστον 1/s γρ. δηλητήριο το καθένα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 13 Νοεμβρίου, 2013 @ 2:55 πμ
Αν καταλαβαίνω τα άνω (διόρθωσέ με αν κάνω λάθος..) λες το εξής:
Δοθέντων
, θέτουμε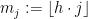 
, για j=1,…,s.
είναι το μέγιστο πλήθος δηλητηριασμένων κουλουρακίων που μπορούμε
![P_j := \mathbb{P}[X_j \geq j]](https://s0.wp.com/latex.php?latex=P_j+%3A%3D+%5Cmathbb%7BP%7D%5BX_j+%5Cgeq+j%5D&bg=ffffff&fg=000000&s=0&c=20201002)
, όπου 
ακολουθεί υπεργεωμετρική κατανομή
.
Δηλ.
να έχουμε, αν χρησιμοποιήσουμε δόσεις 1/j γρ., j=1,…,s.
Στην περίπτωση αυτή, η πιθανότητα «επιτυχίας» ισούται με
παραμέτρων
Τώρα, ο ισχυρισμός του σχολίου (6) λέει ότι
, για κάθε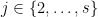 
.
Ο τελευταίος ισχυρισμός είναι αρκετά τεχνικός και δε ξέρω κατά πόσο είναι εύκολο
να αποδειχθεί χωρίς τη βοήθεια υπολογιστικού βοηθήματος..
Αλλά ακόμα κι αν ο ισχυρισμός αυτός είναι αληθής, δεν μας εξασφαλίζει ότι
δεν υπάρχει μια κατανομή δηλητηρίου με ανισόποσες δόσες που να έχει καλύτερη πιθανότητα «επιτυχίας».
ΥΠΟΔΕΙΞΗ: Στην ουσία η υπόδειξη έχει δοθεί σε προηγούμενο σχόλιο από τον Δρ. Γιώργο Ριζόπουλο και είναι το θεώρημα Erdos-Ko-Rado..
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 13 Νοεμβρίου, 2013 @ 1:24 μμ
Ευχαριστώ για το σχόλιό σας, όπως και τον αγαπητό Δρ. Γ. Ριζόπουλο!
Εφόσον η συνολική ποσότητα δηλητηρίου είναι αυστηρά μικρότερη από 2 γρ., είναι επόμενο ότι δεν μπορεί να υπάρχουν δύο διακριτοί / ξένοι μεταξύ τους θανατηφόροι συνδυασμοί από s κουλουράκια, διότι διαφορετικά θα χρειαζόμασταν τουλάχιστον 2 γρ. δηλητηρίου.
Επομένως, όπως και αν μοιράσουμε το διαθέσιμο δηλητήριο, δύο θανατηφόρα υποσύνολα /συνδυασμοί μεγέθους s θα έχουν τουλάχιστον ένα κοινό στοιχείο / κουλουράκι.
Εδώ έρχεται και δένει νομίζω το θεώρημα Erdos-Ko-Rado που μας λέει ότι o μέγιστος αριθμός των τεμνόμενων ανά δύο υποσυνόλων, μεγέθους s, ενός συνόλου μεγέθους n, όταν 2s<=n, είναι C(n-1,s-1) = (n-1)!/[(s-1)!(n-s)!].
Επομένως, η μέγιστη δυνατή απόδοση μιας στρατηγικής κατανομής (σε ίσες ή όχι ποσότητες) του δηλητηρίου σε πολλά κουλουράκια, δεν είναι δυνατό να υπερβεί το: {(n-1)!/[(s-1)!(n-s)!]} / [n!/s!(n-s)!] = s/n.
Αυτό νομίζω ότι αποδεικνύει, επαρκώς πλέον, την υπεροχή της στρατηγικής της τοποθέτησης μιας θανατηφόρας δόσης 1 γρ. σε ένα μόνο κουλουράκι, η οποία αποδίδει πάντα πιθανότητα s/n.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 13 Νοεμβρίου, 2013 @ 9:56 μμ
Ακριβώς.
Όπως και να κατανείμει κανείς το δηλητήριο στα κουλουράκια, η οικογένεια
.
των θανατηφόρων υποσυνόλων πλήθους s είναι τέμνουσα (intersecting)
και το EKR δίδει ότι ο πληθάριθμος μιας τέτοιας οικογένειας είναι το πολύ
Συνεπώς το «να βάλουμε 1 γρ. σε ένα κουλουράκι» είναι βέλτιστο.
Να μία περίπτωση στην οποία δεν εφαρμόζει το EKR.
Υποθέστε ότι
και ότι 
.
Πώς θα "παίζατε" σε αυτή την περίπτωση ;
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 13 Νοεμβρίου, 2013 @ 11:37 μμ
Στην περίπτωση αυτή, νομίζω ότι η βέλτιστη στρατηγική συνδέεται αμεσότερα με την ακριβή τιμή του h και δεν είναι ενιαία σε όλο το διάστημα.
Αν διαθέτουμε τουλάχιστον 1,5 γρ. δηλητήριο, μπορούμε να ρίξουμε από 0,5 γρ. σε 3 κουλουράκια και έτσι κάθε συνδυασμός με 3 κουλουράκια που περιλαμβάνει 2 ή 3 δηλητηριασμένα είναι θανατηφόρος. Τέτοιοι συνδυασμοί είναι 3*2+1=7, επί συνόλου 10, οπότε έχουμε απόδοση 7/10, έναντι 3/5=6/10 που αποδίδει η στρατηγική 1 γρ σε ένα κουλουράκι. Για h>=1,5 κερδίζει λοιπόν η στρατηγική ‘από 0,5 γρ. σε 3 κουλουράκια’
Αν όμως το h είναι λιγότερο από 1,5 γρ., δε μοιράζεται αποτελεσματικά σε 3 κουλουράκια, αφού έτσι προκύπτει μόλις 1 θανατηφόρος συνδυασμός και απόδοση 1/10, ενώ αν μοιραζόταν σε 2, οι θανατηφόροι συνδυασμοί θα έφταναν στους 3 με αντίστοιχη απόδοση 3/10, έναντι 3/5 της στρατηγικής 1 γρ. σε ένα κουλουράκι. Επομένως, για h<1,5 κερδίζει η στρατηγική ΄1 γρ. σε ένα κουλουράκι'.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 14 Νοεμβρίου, 2013 @ 1:02 πμ
Μπράβο στο Θανάση Παπαδημητρίου, για τη δουλειά του και την εξαιρετική προσέγγισή του στο θέμα. Της έδωσε και κατάλαβε της παλιοπεθεράς! (να διευκρινίσω πως δεν είμαι πεθερόπληκτος ,αλλά ίσως αυτό να οφείλεται απλώς στο ότι μας χωρίζει κάποιος σεβαστός αριθμός χιλιομέτρων, οπότε δεν θα πάω κόντρα στη «συλλογική» αντίληψη..):-)
Μπράβο και στον κο Πελέκη για το ωραίο θέμα και την γενικότερη δουλειά του πάνω στα search games και όχι μόνον βέβαια, υποθέτω. Τιμής ένεκεν και «πονηρεμένος» και από το αβατάρι του, που είναι ένας υπεργράφος Pedersen (Pedersen Graph) να πούμε ότι οι επιλογές της πεθεράς για την περίπτωση n=5 και s=3 μπορούν να προσομοιωθούν με τους κόμβους του γραφήματος αυτού (10 συνολικά), όπου κάθε κορυφή αντιστοιχεί στην επιλογή μιας διακριτής τριάδας μπισκότων από τα 1,2,3,4,5, οπότε στην περίπτωση που 1,5<= h 1) είναι (βάσει Schubfachprinzip) τουλάχιστον τρεις (3).
Λίγο μπερδεμένα ίσως τα έγραψα. Το βασικό είναι πως κάθε διαδρομή μήκους 5 ,θα περιέχει τουλάχιστον μία μη-θανατηφόρα κορυφή. Οπότε η κατανομή 1,5 -1,5 -1,5,-0-0 είναι όντως η βέλτιστη.
Για την περίπτωση που h1/2 αφού h<3/2, αλλά τότε αυτό το μπισκότο θα έπρεπε να το έχει κάθε άλλη θανατηφόρα κορυφή, και το φαρμάκι δεν μας φτάνει, άρα όντως το βάζουμε όλο σε μία κορυφή (μπισκότο) και ελπίζουμε να το επιλέξει η καλή μας πεθερούλα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 14 Νοεμβρίου, 2013 @ 10:38 πμ
Συγγνώμη για τη γερμανικούρα (παλιές κακές συνήθειες…) Schubfachprinzip που μου ξέφυγε πριν. Είναι η Αρχή του Περιστερώνα του Ντίριχλετ.
Να διευκρινίσω επίσης, προς αποφυγή παρεξηγήσεων, πως η συνδυαστική προσέγγιση μέσω του Pedersen Graph, δεν ήταν δική μου έμπνευση, αλλά τη βρήκα στο Internet, σε σχετική εργασία του κου Πελέκη , και μην ξέροντας αν θα ήταν πρέπον να δώσω λινκ, έδωσα τη δική μου απόδοση. Εννοείται πως τυχόν λάθος προσεγγίσεις στο απο πάνω σχόλιο είναι αποκλειστικά δική μου ευθύνη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 14 Νοεμβρίου, 2013 @ 10:45 πμ
Τέτοιο ζωντανό θέμα καιρό είχε να δει το blog.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 14 Νοεμβρίου, 2013 @ 10:46 πμ
Ωχ! Bλέπω πως για κάποιον ανεξήγητο για μένα λόγο, το σχόλιό μου 13 . εμφανίστηκε σοβαρά πετσοκομμένο και ως εκ τούτου είναι μάλλον ακατανόητο, συγγνώμη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 14 Νοεμβρίου, 2013 @ 11:39 πμ
Επιτρέψτε μου να κρατήσω το θέμα ζωντανό για λίγο ακόμα..
Δοκιμάστε να βρείτε τη βέλτιστη κατανομή δηλητηρίου στην ακόλουθη περίπτωση:
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 14 Νοεμβρίου, 2013 @ 3:29 μμ
Για να αποφευχθεί η περίπτωση παρανόησης, να σημειώσω ότι η φράση
«βρείτε τη βέλτιστη κατανομή δηλητηρίου» στο άνω σχόλιο είναι, κάπως, καταχρηστική..
Η βέλτιστη κατανομή δεν είναι μοναδική. Αυτό μπορεί να το δεί κανείς και στην περίπτωση
που εφαρμόζει το EKR. Είναι βέλτιστο «να βάλουμε 1γρ. σε ένα κουλουράκι», αλλά είναι
επίσης βέλτιστο «να βάλουμε 1+ε γρ. σε ένα κουλουράκι». Το βέλτιστο αναφέρεται στη
πιθανότητα «επιτυχίας» της κατανομής δηλητηρίου..
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 14 Νοεμβρίου, 2013 @ 6:26 μμ
Σας ευχαριστώ για τα σχόλια, ιδιαίτερα (επιτρέψτε μου) το φίλο Γ. Ριζόπουλο για τις καίριες και ουσιαστικές του παρεμβάσεις (φυσικά και για τα καλά του λόγια!)
Για τη νέα παραλλαγή, θα επιχειρήσω προς το παρόν μια εκτίμηση, που ανεξαρτήτως τού πόσο εύκολα αποδεικνύεται, νομίζω ότι δύσκολα διαψεύδεται.
Εδώ φυσικά θα ήταν προφανής ανοησία να βάλει κανείς 1 γρ. δηλητήριο σε ένα μόνο κουλουράκι, αφού έχει αρκετό για να βάλει από 1 γρ. σε δύο κουλουράκια. Λιγότερο προφανής είναι ίσως η υπεροχή της στρατηγικής ‘από 1 γρ. σε δύο κουλουράκια’ απέναντι σε όλες τις εναλλακτικές στρατηγικές κατανομής του δηλητηρίου σε περισσότερα, πιστεύω όμως ότι είναι πάντα κυρίαρχη, με απόδοση:
p = [(2k-1)s+1[ / [k(ks+1)].
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 14 Νοεμβρίου, 2013 @ 11:18 μμ
Για το πρόβλημα 17. :
Με βάση ό,τι είδαμε ως τώρα ,κι αφού προφανώς αν sh/n ≥1 δεν τίθεται θέμα, αφού μοιράζοντας ισόποσα σε n μπισκότα-κόμβους ποσότητα n/h δηλητηρίου ,εξασφαλίζουμε πάντα θανατηφόρα υποσύνολα s (υπερακμές hyperedges με ορολογία υπεργράφων) ,το πρόβλημα -στη γενική μορφή του- υφίσταται μόνο για h≥1 (προφανώς) και για sh/n ≤1
H οικογένεια, έστω F(n) όλων των υποσυνόλων s του συνόλου Ν={1,2,…,n-1,n} είναι ,όπως ανέφερε ήδη και ο κος Πελέκης, ένας υπεργράφος (hypergraph) οπότε εφεξής είναι δόκιμο να θεωρούμε το πρόβλημα ως: στοιχεία(μπισκότα) του Ν = κόμβοι και τα θανατηφόρα (ή μη) υποσύνολα πλήθους s = «υπερακμές» ή σκέτο ακμές (edges),δηλαδή διαδρομές(επιλογές) που συνδέουν κόμβους(μπισκότα) Και το δηλητήριο κάθε κορυφής n(i) ας το συμβολίσω δ(1),…δ(n)
Mε βάση λοιπόν το γενικο «περιορισμο» sh/n ≤1 θα υπάρχουν πάντα συνδυασμοί των δ που θα δίνουν θανατηφόρα και μη θανατηφόρα υποσύνολα. Συμβολίζω sΘ και sMΘ αντίστοιχα.
Με βάση τα παραπάνω αν η οικογένεια F(n) των s είναι τέμνουσα(intersecting) ,εφόσον n=ks+1 —>2s < n άρα (βάσει Θεωρ. Ε-Κ-R) έχει το πολύ C(n-1, s-1) στοιχεία. Στην περίπτωσή μας ,για h h-2 ;
Σ’αυτήν την περίπτωση η οικογένεια των sΘ που δεν περιέχουν τον κόμβο n, σχηματίζουν μια τέμνουσα F(n). Aπό ΕΚΡ έχουμε λοιπόν:
|F(n)| ≤ C(n-1-1 , s-1)=C(n-2 ,s-1)
O k;oμβος n περιέχεται σε C(n-1,s-1) ακμές ,έτσι ο μέγιστος δυνατός αριθμός θανατηφόρων ακμών είναι:
C(n-1, s-1)+ C(n-1,s-1) = C(n,s) – C(n-2,s) που είναι ακριβώς ο αριθμός των θανατηφόρων ακμών που δημιουργούνται αν βάλουμε 2 κόμβους (μπισκότα) με δ1=δ2= 1γραμμάριο. ,όπως είπε και ο Θ. Παπαδημητρίου.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 15 Νοεμβρίου, 2013 @ 10:53 πμ
Πάλι μαντάρα εμφανίστηκε το σχόλιο. Μάλλον φταίνε κάποια σύμβολα που χρησιμοποιώ ,δεν ξέρω…
Κάνω μια ακόμη προσπάθεια, να αποσαφηνίσω τα ομιχλώδη.,χρησιμοποώντας περίφραση..
Για h μεγ.ή ίσον 2 ,και h = 1/s αλλιώς καμιά ακμή δεν είναι Θ.
Αν h-δ(n) < 2 η οικογένεια των Θ.ακμών (sΘ) που ΔΕΝ περιέχουν τον κόμβο n συνιστούν μια τέμνουσα οικογένεια F.
Aπό το θεωρ. ΕΚΡ έχουμε: πληθάριθμος του Εφ μικρ.ή ίσος του διωνυμικού συντ. (n-2 , s-1)
Yp;arxoyn C (n-1 ,s-1) ακμές που δεν περιέχουν τον κόμβο n ,έτσι ο μέγιστος δυνατός αριθμός θανατηφόρων ακμών είναι
C(n-2, s-1)+ C(n-1,s-1) = C(n,s) – C(n-2,s)
Aρα, 2 δόσεις του 1 γραμ. = βέλτιστο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 15 Νοεμβρίου, 2013 @ 11:46 πμ
Στο paper αυτό: http://arxiv.org/pdf/1107.5544.pdf (Θεώρημα 1.2 και συναφή) βλέπω ότι το Ε-K-R μπορεί να γενικευτεί και να καλύψει
ένα εύρος περιπτώσεων πεθεροδηλητηρίασης.
Υπάρχει, για καθε τριάδα ακεραιων n,s,t o μέγιστος δυνατός πληθάρθμος της Ενωσης των s υποσυνόλων, εκ των οποίων δεν υπάρχουν t ανά δύο μεταξύ τους disjoint, και τα οποία επιλέγονται από ενα σύνολο μεγέθους n.
Aν, έστω Α αυτός ο αριθμός , η τροποποιημένη/γενικευμένη εκδοχή του ΕΚR λέει ότι:
A= C(n,s) -C(n-t+1 , s) για κάθε n > από κάποιο όριο/σταθερά που -αν έχω καταλάβει σωστά το πέηπερ που αναφέρω- έχει ανω όριο το 2s^3, και εξαρτάται ασφαλώς από τις τιμές s και t.
Aν το t στην περίπτσωσή μας ισούται με floor(h) τότε ο μέγιστος αριθμός sΘ φράσεται άνω από τον αριθμό Α. Αλλά το A= C(n,s) -C(n-t+1 , s)
αντιστοιχεί στην οικογένεια των s υποσυνόλων που περιέχουν τουλάχιστον ένα στοιχείο από κάποιο δεδομένο υποσύνολο μεγέθους t-1
Aυτό σημαίνει ΄πως το βέλτιστο είναι «μοναδιαία » δηλητηριώδη μπισκότα. (όπως στην ειδική περίπτωση του θέματος 17.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Rizopoulos Georgios — 15 Νοεμβρίου, 2013 @ 1:36 μμ
Επέτρεψέ μου να γράψω το επιχείρημα των σχολίων (20) και (21) σε Latex για να φανεί καλύτερα.
Είναι σαφές ότι, σε μια βέλτιστη κατανομή δηλητηρίου, θα πρέπει να υπάρχει κουλουράκι
γραμμάρια διότι σε αντίθετη περίπτωση δεν μπορούμε να δηλητηριάσουμε την πεθερά.
και έστω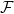 
η οικογένεια που
που είναι θανατηφόρα.
.
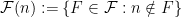που περιέχει
Έστω ότι το κουλουράκι αυτό είναι το
αποτελείται από τα υποσύνολα πλήθους
Έστω επίσης
Η υπόθεση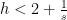
δίδει ότι η 
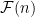είναι τέμνουσα και με χρήση του EKR συμπεραίνουμε ότι
Συνεπώς το "να βάλουμε 1γρ. σε δύο κουλουράκια" είναι βέλτιστο.
Μέχρις αυτό το σημείο έχω καταφέρει κι εγώ να "σπρώξω" EKR..
Όπως λες και το σχόλιο (22) η γενική περίπτωση του προβλήματος
σχετίζεται με ένα ανοικτό πρόβλημα από τη θεωρία υπεργραφημάτων
που, σε διεθνή γλώσσα, αποκαλείται "Erdos' matching conjecture".
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 15 Νοεμβρίου, 2013 @ 2:40 μμ
Εξαιρετικά τα τελευταία σχόλια / λύσεις και αυτής της παραλλαγής. Ευχαριστώ και συγχαίρω τον κ. Πελέκη για την επιλογή του θέματος και την παρουσίαση τής λύσης του, ιδιαιτέρως όμως τον ‘υπερβράχο’ Γ. Ριζόπουλο (ο χαρακτηρισμός δεν έχει καμία σχέση με τους γράφους, είναι απλά ο υπερθετικός του ογκόλιθου) για τη λύση, τα σχόλια και τις προεκτάσεις που έδωσε.
Φυσικά έχω καλυφθεί απόλυτα, αλλά μιας και δεν είχα την ευχέρεια συμμετοχής στο πρωινό live, επιτρέψτε μου μια τελευταία πινελιά, για την απόδοση της λύσης σε μια κάπως λιγότερο μαθηματική / τεχνική γλώσσα:
Το ευφυέστατο εύρημα του κουλουρακίου, που περιέχει δηλητήριο τουλάχιστον 1/s γρ., μάς έδωσε τη δυνατότητα να διαιρέσουμε τη μεγάλη οικογένεια των θανατηφόρων συνδυασμών σε δύο ξεχωριστά γκρουπ:
α) το γκρουπ των θανατηφόρων συνδυασμών, s από n, που ΟΛΟΙ ΠΕΡΙΛΑΜΒΑΝΟΥΝ το υπόψη κουλουράκι, άρα είναι εξ ορισμού τεμνόμενοι ανά δύο
β) το γκρουπ των θανατηφόρων συνδυασμών, s από n-1, που κανείς δεν περιλαμβάνει το υπόψη κουλουράκι, αλλά είναι και πάλι αναγκαστικά τεμνόμενοι ανά δύο, αφού η υπολειπόμενη ποσότητα δηλητηρίου, χωρίς το κρίσιμο κουλουράκι, καθίσταται πλέον μικρότερη από 2 γρ.
Έτσι, ενώ η μεγάλη οικογένεια δεν πληρούσε τις προϋποθέσεις υπαγωγής στην αρμοδιότητα του EKR, οι δύο υποοικογένειες τις πληρούν αμφότερες. Τα υπόλοιπα είναι πραξούλες.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟΥ — 15 Νοεμβρίου, 2013 @ 6:59 μμ