Σε κάθε ακέραιο σημείο του επιπέδου , με
, έχουμε κεντράρει ένα δίσκο ακτίνας
γεμάτο με μπλε μελάνι. Έπειτα περιστρέφουμε όλους αυτούς τους δίσκους μαζί γύρω από την αρχή των αξόνων κατά μια ολόκληρη περιστροφή (ούτως ώστε κάθε δίσκος γράφει ένα κύκλο στο επίπεδο και επιστρέφει στην αρχική του θέση). Απ’ όπου περνάει ο κάθε δίσκος αφήνει ένα μπλε ίχνος όπου ακουμπήσει.
Δείξτε ότι υπάρχει κάποια πεπερασμένη ακτίνα ούτως ώστε έξω από τον κύκλο με κέντρο το
και ακτίνα
τα πάντα είναι μπλέ.

Υπόδειξη: Για να εμπνευστείτε δείτε και το παλαιότερο πρόβλημα
και σκεφτείτε λίγο για τη συμπεριφορά των αριθμών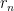 όπου
όπου
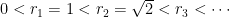
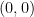 που περνάνε από κάποιο ακέραιο σημείο.
που περνάνε από κάποιο ακέραιο σημείο.
είναι οι ακτίνες όλων των κύκλων με κέντρο το
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Οκτωβρίου, 2012 @ 3:06 μμ
Edaksei, h ypodeiksh ta leei ola… Einai safes oti h a(n)=r(n+1)-r(n) (opou h r(n) h ayksousa akolouthia twn aktinwn) teinei 0 kathws n teinei + apeiro. Ara gia n>N a(n)<ε kai apo ekei kai pera ola einai mple…
Μου αρέσει!Μου αρέσει!
Σχόλιο από fivosk7 — 7 Φεβρουαρίου, 2013 @ 2:54 μμ
Ακριβώς.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 7 Φεβρουαρίου, 2013 @ 4:01 μμ
Η λύση η οποία σκέφτηκα είναι η εξής.
Αρκεί μετά την περιστροφή να έχει χροματιστεί ολόκληρος ο x’x άξωνας εκτός απο μια περιοχή με κέντρο το 0. Στον χ λοιπόν άξωνα θα βρεθούν τα κέντρα τον μικρών κύκλων μετά απο περιστροφή και συγκεκριμένα θα είναι στισ θέσεις sqrt(n^2+k^2) όπου ν είναι η τετμημένη κ k η τεταγμένη με 0<=k0 τέτοιο ώστε η ένωση να έχει την προηγούμενη μορφή. Ακόμα γνωρίζω πως sqrt(n^2 + k^2) 0 n0: για κάθε n>=n0 να ισχύει sqrt(n^2 + (k+1)^2 – sqrt(n^2 + k^2) <= 2e για κάθε k (με 0<=k<=n)
Αυτό όμως είναι ισοδύναμο με το να δείξω οτι το όριο αυτής της διαφοράς καθώς το n πάει στο άπειρο υπάρχει και είναι ίσο με το 0 κάτι που είναι ολοφάνερο οτι ισχύει.
Να συμμειωθεί ότι δεν χρεισημοποιήθηκαι η υπόδηξη για την λύση της άσκησης. Συγγνώμη για την άσχημη γραφή αλλά δεν γνωρίζω πώς να εισάγω μαθηματικά σύμβολα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Charidimos Kiosterakis — 17 Μαΐου, 2013 @ 4:09 μμ
Πιθανότατα σωστό, αλλά δοκίμασε σε παρακαλώ να το ξαναγράψεις πιο καθαρά γιατί δε βγάζω εύκολα νόημα (και φαντάζομαι και οι υπόλοιποι αναγνώστες).
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 20 Μαΐου, 2013 @ 12:07 μμ
Αυτό που ισχυρίζομαι είναι πως δεν χρειάζεται να βρούμε μια αύξουσα διάταξη ακτίνων απλά αρκεί το γεγονός ότι για μεγάλα n η διαφορά των ακτίνων sqrt(n^2 + k^2) και sqrt(n^2 + (k+1)^2) να μπορεί να είναι μικρότερη απο 2e που ισχύει απο ένα n1 και έπειτα. Αυτό εξασφαλίζει πως το διάστημα [n, n*sqrt(2)] στον άξωνα χ’χ θα βαφτεί μπλε. Όμως και το διάστημα [n+1, (n+1)*sqrt(2)] στον χ’χ θα είναι μπλε. Για μεγάλα όμως n (έστω μεγαλύτερα από n2) τα διαστήματα έχουν μη μιδενική τομή (ισχύει τελικά ότι n*sqrt(2)>= n+1). Τώρα για n>= max{n1,n2} θα ισχύουν και τα δύο οπότε από εκεί και πέρα ο χ’χ θα είναι όλος μπλέ. Αφού όμως ο χ’χ είναι μπλέ θα υπάρχει ακτίνα R ούτως ώστε έξω από τον κύκλο με κέντρο το (0,0) και ακτίνα R τα πάντα είναι μπλέ. Δεν μπορώ να το εξηγήσω καλύτερα χωρίς σχήμα και χωρίς χαρτί, νομίζω αυτή την φορά να έγινε περισσότερο κατανοητό. Την ιδέα σας την είχα αναφέρει και στο γραφείο σας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Charidimos Kiosterakis — 21 Μαΐου, 2013 @ 1:45 πμ
Το διάστημα![[n, n\sqrt{2}]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n%5Csqrt%7B2%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) πώς προέκυψε;
πώς προέκυψε;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 23 Μαΐου, 2013 @ 11:17 πμ
Αν πάρω τον κύκλο με κέντρο (n,0) και τον περιστρέψω τότε θα βαφτεί στον χ’χ το διάστημα [n-ε,n+ε], αν πάρω τώρα τον κύκλο με κέντρο (n,1) και το περιστρέψω θα βαφτεί και το διάστημα [sqrt(n^2 + 1) – ε, sqrt(n^2 +1) – ε] στον χ’χ…. Τέλος αν πάρω και τον κύκλο κέντρου (n,n) θα βαφτεί και το διάστημα [n*sqrt(2) – ε, n*sqrt(2) + ε] του χ’χ. Όμως έχω πεί ότι η ένωση αυτών των διαστημάτων δήνει διάστημα οπότε θα πάρω ότι το διάστημα [n – ε, n*sqrt(2) + ε] είναι μπλε και απο εδώ προκύπτει το [n, n*sqrt(2)]. Έγινα κατανοϊτός?
Μου αρέσει!Μου αρέσει!
Σχόλιο από Charidimos Kiosterakis — 23 Μαΐου, 2013 @ 7:36 μμ
Μια χαρά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 26 Μαΐου, 2013 @ 2:41 πμ
Ευχαριστώ
Μου αρέσει!Μου αρέσει!
Σχόλιο από Charidimos Kiosterakis — 27 Μαΐου, 2013 @ 12:17 πμ