Στεκόμαστε στο σημείο (0, 0) του επιπέδου και κοιτάμε γύρω μας τα ακέραια σημεία του επιπέδου, τα σημεία δηλ. που έχουν και τις δύο συντεταγμένες τους ακέραιες. Αν είναι δύο τέτοια σημεία και
για κάποιο
τότε το σημείο
είναι αόρατο σε μας (αφού η ακτίνα του φωτός που ξεκινάει από αυτό και κατευθύνεται προς εμάς κόβεται στο σημείο
που βρίσκεται ανάμεσά μας).
Δείξτε ότι το σύνολο των αόρατων ακέραιων σημείων του επιπέδου περιέχει οσοδήποτε μεγάλα κομμάτια, περιέχει δηλ., για κάθε ένα σύνολο της μορφής
για κατάλληλα επιλεγμένα ακέραια .
Για να λυθεί το πρόβλημα αρκεί να βρούμε φυσικούς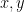 έτσι ώστε οι
έτσι ώστε οι 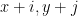 να μην είναι πρώτοι μεταξύ τους για
να μην είναι πρώτοι μεταξύ τους για 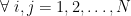
 έτσι ώστε οι
έτσι ώστε οι 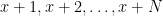 να διαιρούνται ο καθένας από τουλάχιστο
να διαιρούνται ο καθένας από τουλάχιστο  διαφορετικούς πρώτους.
διαφορετικούς πρώτους.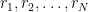 επαγωγικά ως εξής:
επαγωγικά ως εξής:

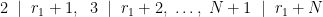 .
.
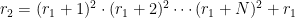
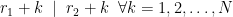 .
.
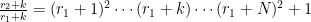
 διαιρείται από τουλάχιστο
διαιρείται από τουλάχιστο  διαφορετικούς πρώτους για
διαφορετικούς πρώτους για 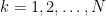 .
.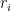 έτσι ώστε οι
έτσι ώστε οι  να διαιρούνται από τουλάχιστο
να διαιρούνται από τουλάχιστο  διαφορετικούς πρώτους για
διαφορετικούς πρώτους για 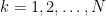 ,ορίζουμε
,ορίζουμε
 .
.
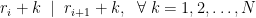 .
.
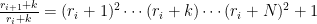
 διαιρείται από τουλάχιστο
διαιρείται από τουλάχιστο  διαφορετικούς πρώτους για
διαφορετικούς πρώτους για 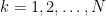 (αφού οι πρώτοι που διαιρούν τον
(αφού οι πρώτοι που διαιρούν τον 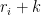 δεν διαιρούν τον
δεν διαιρούν τον  ).
).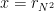 .
.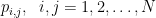 διαφορετικοί ανά δύο έτσι ώστε για
διαφορετικοί ανά δύο έτσι ώστε για  .
. έτσι ώστε
έτσι ώστε

 άρα τα
άρα τα  είναι αόρατα ακέραια σημεία του επιπέδου.
είναι αόρατα ακέραια σημεία του επιπέδου.
Πρώτα επιλέγουμε τον
Επιλέγουμε φυσικούς αριθμούς
οπότε
Στο δεύτερο βήμα ορίζουμε
οπότε
Επιπλέον αφού
ο
Επαγωγικά αν οριστεί ο
Τότε
Επιπλέον αφού
ο
Θέτουμε
Υπάρχουν πρώτοι
Τώρα από το Κινέζικο Θεώρημα μπορούμε να επιλέξουμε
Τότε
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 14 Ιανουαρίου, 2012 @ 10:15 μμ
Δε μπορώ να δω κάτι.
Για τα βλέπω ότι είναι διαφορετικά μεταξύ τους αλλά όχι αν αλλάξει και ο πρώτος δείκτης. Για παράδειγμα, γιατί είναι τα
βλέπω ότι είναι διαφορετικά μεταξύ τους αλλά όχι αν αλλάξει και ο πρώτος δείκτης. Για παράδειγμα, γιατί είναι τα  διαφορετικά;
διαφορετικά;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 15 Ιανουαρίου, 2012 @ 10:32 μμ
Στη γραμμη του
γραμμη του  σχολιου ειναι καλύτερα να έλεγα:
σχολιου ειναι καλύτερα να έλεγα: επιλέγουμε τον ακέραιο
επιλέγουμε τον ακέραιο 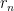 επαγωγικά ως εξής: »
επαγωγικά ως εξής: » γίνεται ως εξής:
γίνεται ως εξής: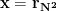 οπότε οι ακέραιοι
οπότε οι ακέραιοι  διαιρούνται ο καθένας από τουλάχιστο
διαιρούνται ο καθένας από τουλάχιστο 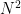 διαφορετικούς πρώτους(Εμάς μας ενδιαφέρει μόνο για τους
διαφορετικούς πρώτους(Εμάς μας ενδιαφέρει μόνο για τους 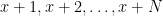 ).
).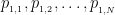 τυχαια από τους πρώτους που διαιρούν τον
τυχαια από τους πρώτους που διαιρούν τον 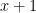 .
.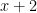 (οι οποίοι είναι τουλάχιστο
(οι οποίοι είναι τουλάχιστο 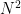 στο πλήθος) επιλέγουμε τους
στο πλήθος) επιλέγουμε τους 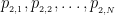 ετσι ώστε οι
ετσι ώστε οι  να είναι διαφορετικοί ανά δυο.
να είναι διαφορετικοί ανά δυο.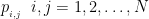 ετσι ώστε να είναι διαφορετικοί ανά δύο.
ετσι ώστε να είναι διαφορετικοί ανά δύο.
» Για
Τώρα η επιλογή των
Θέσαμε
Επιλέγουμε τους
Μετά από τους πρώτους που διαιρούν τον
Συνεχίζοντας επαγωγικά επιλέγουμε τους
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 16 Ιανουαρίου, 2012 @ 3:34 μμ
Σωστά, όλα καλά τώρα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 16 Ιανουαρίου, 2012 @ 4:25 μμ