Δείξτε ότι το δεκαδικό ανάπτυγμα κάποιας δύναμης τού 2 ξεκινάει με τα ψηφία 2011.
16 Ιουνίου, 2011
3 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Δείξτε ότι το δεκαδικό ανάπτυγμα κάποιας δύναμης τού 2 ξεκινάει με τα ψηφία 2011.
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Το 2011 δεν έχει κάτι μαγικό και μπορεί να αντικατασταθεί από την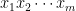 .
.
 είναι η απεικόνιση που ορίζεται ως
είναι η απεικόνιση που ορίζεται ως
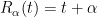 (mod 1), η τροχιά
(mod 1), η τροχιά 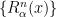 οποιουδήποτε
οποιουδήποτε 
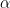 είναι άρρητος.
είναι άρρητος.
αγαπημένη σας αράδα αριθμών
Θυμηθείτε ότι, αν
είναι ο μοναδιαίος κύκλος και
είναι πυκνή, αν ο
Παρατηρείστε ότι το ξεκινάει με τα ψηφία
ξεκινάει με τα ψηφία 

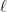 ώστε
ώστε
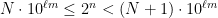 .
. υπάρχουν αν και μόνον αν
υπάρχουν αν και μόνον αν
 ή
ή
 (mod 1).
(mod 1). .
.
αν και μόνον αν υπάρχει k τέτοιο ώστε
και το πρόβλημα ανάγεται στην εύρεση τέτοιου k, το οποίο ψάχνουμε ανάμεσα στα
πολλαπλάσια του m. Δηλαδή ενδιαφερόμαστε για την ύπαρξη κάποιου
Τέτοια
Το ζητούμενο έπεται από το γεγονός ότι
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 22 Ιουνίου, 2011 @ 9:41 μμ
Νομίζω οτι είναι πρέπον να πω πως ‘έκλεψα’ το άνω επιχείρημα από το (δύσκολο !) βιβλίο
Εργοδικής θεωρίας των M. Einsiedler & T. Ward στο οποίο εμφανίζεται ως άσκηση.
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 22 Ιουνίου, 2011 @ 9:52 μμ
Σωστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 22 Ιουνίου, 2011 @ 10:07 μμ