Έστω η ακολουθία όλων των πρώτων αριθμών και ας θεωρήσουμε μια ακολουθία
από σύνθετους αριθμούς που είναι μεταξύ τους σχετικά πρώτοι:
. Συγκλίνει η σειρά
6 Φεβρουαρίου, 2010
Συγκλίνει;
4 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Αν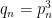 τότε ικανοποιούνται οι υποθέσεις για την
τότε ικανοποιούνται οι υποθέσεις για την 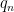 και η σειρά δεν συγκλίνει.
και η σειρά δεν συγκλίνει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 7 Φεβρουαρίου, 2010 @ 4:50 μμ
Σ’ αυτήν την περίπτωση αποκλίνει. Αποκλίνει όμως σε κάθε περίπτωση… αυτό θα θέλαμε να δείξουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 7 Φεβρουαρίου, 2010 @ 10:48 μμ
Τα γραμματα θα δηλωνουν απολυτες σταθερες (οχι απαραιτητα τις ιδιες καθε φορα).
θα δηλωνουν απολυτες σταθερες (οχι απαραιτητα τις ιδιες καθε φορα).
Θα θεωρησω ως δεδομενο οτι
Τοτε εχουμε οτι
Εστω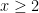 . Εστω οτι
. Εστω οτι 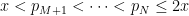 ειναι ολοι οι πρωτοι στο διαστημα
ειναι ολοι οι πρωτοι στο διαστημα ![(x,2x]](https://s0.wp.com/latex.php?latex=%28x%2C2x%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Τοτε θα εχουμε οτι
. Τοτε θα εχουμε οτι
Οντως, αν γραψουμε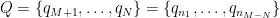 , οπου ο
, οπου ο  εχει το μικροτερο πρωτο διαιρετη απο ολα τα στοιχεια του
εχει το μικροτερο πρωτο διαιρετη απο ολα τα στοιχεια του 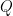 , ο
, ο 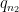 εχει το δευτερο μικροτερο πρωτο διαιρετη και ουτω καθ'εξης, τοτε θα εχουμε οτι
εχει το δευτερο μικροτερο πρωτο διαιρετη και ουτω καθ'εξης, τοτε θα εχουμε οτι  , καθως οι αριθμοι
, καθως οι αριθμοι  ειναι αμοιβαια πρωτοι και συνθετοι αριθμοι.
ειναι αμοιβαια πρωτοι και συνθετοι αριθμοι.
Επομενως, η (2) συνεπαγεται οτι
καθως απο την (1).
απο την (1).
Αρα
Η παραπανω ανισοτητα συνεπαγεται οτι
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 15 Φεβρουαρίου, 2010 @ 2:01 πμ
Η λύση σου είναι σωστή.
Υπάρχει όμως και μια στοιχειώδης απόδειξη που αποφεύγει την επίκληση του θεωρήματος πυκνότητας των πρώτων αριθμών. Μπορεί να βασιστεί στην ειδική περίπτωση του θεωρήματος αναδιάταξης που αναφέρεται στην υπόδειξη του προβλήματος «Ανισότητα Αναδιάταξης«.
Αναδιατάξτε τους σε αύξουσα σειρά:
σε αύξουσα σειρά:  . Δεν είναι δύσκολο να δείτε (γιατί;) ότι έχουμε
. Δεν είναι δύσκολο να δείτε (γιατί;) ότι έχουμε  . Επομένως, από την εν λόγω ανισότητα έχουμε
. Επομένως, από την εν λόγω ανισότητα έχουμε

Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 15 Φεβρουαρίου, 2010 @ 7:40 μμ