Εργάζεστε στο Υπουργείο Οικονομικών και παίρνετε εντολή να επιλέξετε ένα τυχαίο δείγμα επαγγελματιών για φορολογικό έλεγχο. Ο προϊστάμενός σας έχει θέσει αυστηρές προδιαγραφές:
- Κάθε επαγγελματίας θα πρέπει να ελεγχθεί με πιθανότητα
.
- Η πιθανότητα που έχει κάθε ένας να ελεγχθεί δεν εξαρτάται από το αν κάποιοι άλλοι θα ελεγχθούν ή όχι (σε πιο μαθηματική γλώσσα, τα ενδεχόμενα ελέγχου των επαγγελματιών είναι ανεξάρτητα).
Βλέπετε ότι υπάρχουν επαγγελματίες. Κατ’ αρχήν λοιπόν σκέφτεστε να βάλετε τον υπολογιστή σας να κάνει
τυχαίες και ανεξάρτητες επιλογές και έτσι να επιλέξετε το δείγμα σας. Ο υπολογιστής σας μπορεί φυσικά εύκολα να το κάνει αυτό: είναι εφοδιασμένος με ένα υποπρόγραμμα το οποίο, κάθε φορά που καλείται, επιστρέφει ένα αριθμό
ομοιόμορφα κατανεμημένο στο διάστημα
. Καλείτε λοιπόν αυτό το υποπρόγραμμα
φορές και, κάθε φορά, αν το
πέσει στο διάστημα
τότε ο «τυχερός» επαγγελματίας επιλέγεται για έλεγχο.
Όμως, σας λέει ο έμπειρος προϊστάμενός σας (ο οποίος μόλις είχε πάρει μεταγραφή στο Υπουργείο Οικονομικών από τη Στατιστική Υπηρεσία, η οποία εκείνη την εποχή υπόκειτο σε ανακατατάξεις και δικαστικούς ελέγχους), υπάρχει και η εξής παράμετρος: το σύστημα επιλογής σας υπόκειται σε δικαστικό έλεγχο. Και είναι γνωστό ότι οι υπολογιστές είναι ντετερμινιστικά μηχανήματα και τίποτα από αυτά που κάνουν δεν είναι τυχαίο. Η υπορουτίνα τυχαίων αριθμών που χρησιμοποιείτε δεν παράγει πραγματικά τυχαίους αριθμούς· αυτό όλοι το γνωρίζουν. Πώς μπορεί λοιπόν να σταθεί στο δικαστήριο η μέθοδός σας;
Η μόνη λύση που σας έρχεται στο μυαλό είναι να χρησιμοποιήσετε γεννήτρια τυχαίων αριθμών εκτός του υπολογιστή σας. Ένας τρόπος π.χ. να το κάνετε αυτό είναι να παράγετε πολλά ανεξάρτητα τυχαία νούμερα ομοιόμορφα στο (π.χ. χρησιμοποιώντας κάτι σα ρουλέτα στην οποία μετράτε κάθε φορά τη γωνία με την οποία περιστράφηκε και διαιρείτε διά
) και να τα καταχωρήσετε σε ένα αρχείο του υπολογιστή σας. Όποτε το πρόγραμμά σας χρειάζεται ένα τυχαίο αριθμό απλά θα παίρνει τον επόμενο απο αυτό το αρχείο.
Ο προιστάμενός σας είναι ευχαριστημένος: η μέθοδός σας σίγουρα περνάει κάθε νομικό έλεγχο.
Όμως μετά από λίγο καταλαβαίνετε ότι το να παράγετε τυχαίους αριθμούς με μηχανικό τρόπο θα πάρει πολύ χρόνο και χρήμα. Είναι πρακτικά αδύνατο.
Πρέπει να βρείτε ένα τρόπο να παράγετε αυτό το τυχαίο δείγμα (κατά μέσο όρο θα έχει μέγεθος 100) χρησιμοποιώντας πολύ λιγότερους τυχαίους αριθμούς.
Προτείνετε λύσεις.

Εάν είναι κοντά σε ένα busy web server, να ανοίξει ένα tcpdump και να διαβάζει τους TCP sequence numbers στα πακέτα SYN. Ας το συνδιάσει και με την ώρα άφιξής τους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από adamo — 5 Φεβρουαρίου, 2010 @ 1:46 πμ
Αυτό έχει χίλια μειοενεκτήματα.
Αν κάποιος κακόβουλος ξέρει το πώς δουλεύει το πρόγραμμα επιλογής (και μην ξεχνάμε ότι η κυβέρνηση φαίνεται να κλίνει προς open source λύσεις) τότε μπορεί να επηρεάσει την επιλογή τυχαίων αριθμών με κατάλληλα requests στο server.
Όμως ο σκοπός του προβλήματος δεν είναι να προτείνουμε νέες πηγές τυχαιότητας που να είναι γρήγορες. Υποθέστε ότι η πρόσβαση σε τυχαίους αριθμούς είναι «ακριβή» και προσπαθείστε να την ελαχιστοποιήσετε.
Αλλά και η πρόβαση σε τυχαίους αριθμούς να ήταν γρήγορη, για να δείτε ότι ο πρώτος τρόπος που σκέφθηκε (περνάω έναν-έναν τους επαγγελματίες και αποφασίζω για τον καθένα χωριστά) δεν είναι αποδεκτός, απλά μεταφερθείτε σε μια μεγαλύτερη χώρα, π.χ. τις Η.Π.Α. (όπου παρεπιπτόντως το έλλειμα του ομοσπονδιακού προϋπολογισμού για το 2009 είναι σχεδόν όσο και το δικό μας, 10% του ΑΕΠ) και σκεφθείτε ότι έχετε να ελέγξετε 30 εκατομμύρια επαγγελματίες για να διαλέξετε 2-3 χιλιάδες. Δεν είναι κρίμα να καταβάλετε κόπο ανάλογο του «30 εκατομμύρια» και όχι ανάλογο του «2-3 χιλιάδες»;
Λίγο πιο αυστηρά, ο πρώτος τρόπος που προτάθηκε παίρνει χρόνο ανάλογο του , όσο μικρή και να είναι η πιθανότητα επιλογής
, όσο μικρή και να είναι η πιθανότητα επιλογής  . Αυτό μπορεί να βελτιωθεί σημαντικά.
. Αυτό μπορεί να βελτιωθεί σημαντικά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Φεβρουαρίου, 2010 @ 2:00 πμ
Νομίζω δεν έγινα κατανοητός. Όχι δεν θα πάρεις N μετρήσεις για Ν επαγγελματίες. Εφόσον είναι N, είναι και enumerated από 1..N. Αυτό που χρειάζεται είναι τυχαία νούμερα σε αυτό το διάστημα για το πλήθος δείγματος που θέλει. Καταλαβαίνω κάτι λάθος;
Μου αρέσει!Μου αρέσει!
Σχόλιο από adamo — 5 Φεβρουαρίου, 2010 @ 12:47 μμ
Είναι λίγο λεπτό το σημείο και έχει να κάνει με την απαίτηση της ανεξαρτησίας.
Πόσα τυχαία νούμερα από 1 έως Ν θα πάρεις; Τη μέση τιμή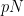 ; Οποιαδήποτε τιμή και να προαποφασίσεις για το πόσους επαγγελματίες θα επιλέξεις θα έχεις παραβιάσει την αρχή της ανεξαρτησίας που απαιτεί ο προϊστάμενος.
; Οποιαδήποτε τιμή και να προαποφασίσεις για το πόσους επαγγελματίες θα επιλέξεις θα έχεις παραβιάσει την αρχή της ανεξαρτησίας που απαιτεί ο προϊστάμενος.
Γιατί αν ο αριθμός αυτών που παίρνεις είναι σταθερός τότε αν γνωρίζεις, π.χ., ότι έχει επιλεγεί ο 1ος, τότε αυτό μειώνει τις πιθανότητες του να επιλεγεί ο 2ος, σε σχέση πάντα με το αν δεν ξέρεις τίποτα για τον πρώτο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Φεβρουαρίου, 2010 @ 1:18 μμ
Με «τρώει» να απαντήσω pN. Κυρίως επειδή το σενάριο βγάζει τον Μηχανικό μέσα μου, με αποτέλεσμα το μέγεθος του προβλήματος να καθορίζει το πως θα αναζητήσω τη λύση του. Γιατί ακόμα και οι δειγματοληπτικοί έλεγχοι δεν γίνονται στο σύνολο των επαγγελματιών, αλλά στο υποσύνολο που δεν υπακούει σε μια κατανομή, ένα υπουργείο Οικονομικών μπορεί να επενδύσει σε ένα δικό του μηχανισμό τυχαιότητας σαν τον http://www.random.org κ.ο.κ, με αποτέλεσμα να πρέπει να μπαίνουν νέα τεχνητά «ακριβά» όρια. Ή θα έπαιρνα ένα (πραγματικά) τυχαίο αριθμό και μια από τις γεννήτριες του L’Ecuyer και τις πρώτες pN μετρήσεις. Ναι έχει πρόβλημα γιατί κάποιος αριθμός μπορεί να επανεμφανιστεί, οπότε οι «τυχεροί» θα είναι το πολύ pN.
Οπότε μπορώ να έχω μια περιγραφή του προβλήματος χωρίς το σενάριο; Από ένα σύνολο N στοιχείων θέλω να επιλέξω με τυχαίο τρόπο τι;
Μου αρέσει!Μου αρέσει!
Σχόλιο από adamo — 9 Φεβρουαρίου, 2010 @ 1:30 πμ
Θέλεις να επιλέξεις ένα υποσύνολο ώστε η πιθανότητα να επιλεγεί κάθε άτομο να είναι και ταυτόχρονα να υπάρχει ανεξαρτησία. Η οποία δεν υπάρχει αν το πλήθος των επιλεγομένων είναι γνωστό εξ αρχής. Αν αυτό το πλήθος είναι, π.χ. 10, και εμείς γνωρίζουμε ότι έχουν επιλεγεί οι εξής 9 μέχρι στιγμής τότε η πιθανότητα να επιλεγεί ο επόμενος είναι πολύ μικρότερη από
και ταυτόχρονα να υπάρχει ανεξαρτησία. Η οποία δεν υπάρχει αν το πλήθος των επιλεγομένων είναι γνωστό εξ αρχής. Αν αυτό το πλήθος είναι, π.χ. 10, και εμείς γνωρίζουμε ότι έχουν επιλεγεί οι εξής 9 μέχρι στιγμής τότε η πιθανότητα να επιλεγεί ο επόμενος είναι πολύ μικρότερη από  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Φεβρουαρίου, 2010 @ 1:42 πμ
[…] Τυχαίοι αριθμοί: Πως μπορούμε να πετύχουμε πραγματικά τυχαίους […]
Μου αρέσει!Μου αρέσει!
Πίνγκμπακ από Το Top 5 της εβδομάδας (14 Φεβρουαρίου – 20 Φεβρουαρίου 2010) | Newsfilter — 21 Φεβρουαρίου, 2010 @ 4:14 μμ
Θα μπορουσαμε να παραγουμε εναν τυχαιο φυσικο αριθμο με δεκαδικα ψηφια. Χωριζουμε τα ψηφια σε τετραδες. Ελεγχουμε τον ν-οστο επαγγελματια αν-ν η ν-οστη τετραδα ειναι 0000.
δεκαδικα ψηφια. Χωριζουμε τα ψηφια σε τετραδες. Ελεγχουμε τον ν-οστο επαγγελματια αν-ν η ν-οστη τετραδα ειναι 0000.
Ως προς την παραγωγη ενος τετοιου αριθμου x, μια ιδεα ειναι να κατασκευασουμε μια ρουλετα μεγαλης διαμετρου την οποια θα χωρισουμε σε κομματια.
κομματια.
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 22 Φεβρουαρίου, 2010 @ 10:49 πμ
Λοιπόν, αν η διακριτική ικανότητα των οργάνων που χρησιμοποιείς είναι ας πούμε 1mm και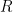 η ακτίνα της ρουλέτας σου τότε, χρησιμοποιώντας την προσέγγιση
η ακτίνα της ρουλέτας σου τότε, χρησιμοποιώντας την προσέγγιση 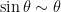 γα μικρές γωνίες, έχεις
γα μικρές γωνίες, έχεις
Το δωμάτιο θα πρέπει να μεγαλώσει πολύ για να τη χωρέσει!
Κάτι πιο πρακτικό χρειάζεται, που δεν υποθέτει την ύπαρξη οργάνων τεράστιας ακρίβειας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Φεβρουαρίου, 2010 @ 11:09 πμ
Λάθος, Τη ρουλέτα πρέπει να τη χωρισουμε σε κομμάτια. Δεν είμαι σίγουρος αν είναι εφικτό να γίνει τόσο ακριβής μέτρηση…
κομμάτια. Δεν είμαι σίγουρος αν είναι εφικτό να γίνει τόσο ακριβής μέτρηση…
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 22 Φεβρουαρίου, 2010 @ 11:09 πμ
Με πρόλαβες με το σχόλιό σου!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Φεβρουαρίου, 2010 @ 11:10 πμ
How about, ένας Ν-μπιτος αριθμός με p-bit στο 1 και τα υπόλοιπα στο 0;
Μου αρέσει!Μου αρέσει!
Σχόλιο από adamo — 22 Φεβρουαρίου, 2010 @ 1:56 μμ
Δεν το κατάλαβα αυτό, τι εννοείς;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Φεβρουαρίου, 2010 @ 1:58 μμ
Έστω το σύνολο των αριθμών μήκους N-bit. Τότε έχεις μια απεικόνιση των N υποψήφιων ανάλογα με το εάν το bit που τους αντιστοιχεί είναι 1 ή 0. Κάποιοι από αυτούς τους αριθμούς έχουν pN άσους (και τα υπόλοιπα bit 0). Διαλέγεις τυχαία έναν από αυτούς τους αριθμούς και οι άσοι (spelling?) σου δίνουν τους «τυχερούς», λόγω της θέσης τους. Δεν έχω υπολογίσει πόσο ακριβό είναι να παράγεις αυτό το σύνολο αριθμών. Βασικά χρειάζεσαι όλες τις τοποθετήσεις pN αντικειμένων (άσοι) σε N θέσεις.
Μου αρέσει!Μου αρέσει!
Σχόλιο από adamo — 22 Φεβρουαρίου, 2010 @ 9:59 μμ
Όχι, δεν πρόκειται να έχεις το ίδιο αποτέλεσμα με ανεξάρτητες αποφάσεις (με πιθανότητα
ανεξάρτητες αποφάσεις (με πιθανότητα  η καθεμία να συμπεριλάβει τον επαγγελματία) αν έχεις προαποφασίσει το πλήθος αυτών που υα επιλεγούν.
η καθεμία να συμπεριλάβει τον επαγγελματία) αν έχεις προαποφασίσει το πλήθος αυτών που υα επιλεγούν.
Αν κανείς διαξάγει το πείραμα ρίχνοντας ένα νόμισμα για τον καθένα τότε το πλήθος αυτών που θα επιλεγούν είναι μεν τυχαίο και έχει μέση τιμή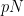 αλλά δεν είναι προαποφασισμένο και κάθε φορά που τρέχουμε το πείραμα είναι εν γένει διαφορετικό.
αλλά δεν είναι προαποφασισμένο και κάθε φορά που τρέχουμε το πείραμα είναι εν γένει διαφορετικό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Φεβρουαρίου, 2010 @ 10:08 μμ
Υπόδειξη:
Ας είναι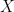 η τυχαία μεταβλητή που παριστάνει το πόσοι τελικά θα ελεγχθούν, αν τους επιλέξουμε με τον τρόπο που απαιτεί η νομοθεσία, αποφασίσουμε δηλ. ανεξάρτητα για τον καθένα.
η τυχαία μεταβλητή που παριστάνει το πόσοι τελικά θα ελεγχθούν, αν τους επιλέξουμε με τον τρόπο που απαιτεί η νομοθεσία, αποφασίσουμε δηλ. ανεξάρτητα για τον καθένα.
Ποια η κατανομή της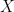 ; Αν η τιμή της
; Αν η τιμή της 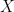 μας είναι γνωστή πώς μπορούμε να παράγουμε το δείγμα (το ποιοι δηλ. είναι αυτοί που θα ελεγχθούν);
μας είναι γνωστή πώς μπορούμε να παράγουμε το δείγμα (το ποιοι δηλ. είναι αυτοί που θα ελεγχθούν);
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 28 Φεβρουαρίου, 2010 @ 11:17 μμ
το ποσοι τελικα θα ελεγθουν δεν ειναι προκαθορισμενο? αφου πρεπει να τους διαλεξουμε με πιθανοτητα 1/10.000 τοτε σε μια λιστα 100.000 ατομων θα επιλεξουμε αναγκαστικα 10 ατομα…..Τωρα αν θελουμε να επεκτεινουμε το δειγμα π.χ στα 50 ατομα επιλεγουμε 1 προς 1 τους τυχερους ΧΩΡΙΣ να αφαιρεσουμε τους ηδη επιλαχθεντες απο την λιστα,οποτε εχουμε σταθερο αριθμο υποψηφιων και αρα σταθερο αριθμο πιθανοτητων για τον καθενα, καθε φορα που <> το πειραμα…
Μου αρέσει!Μου αρέσει!
Σχόλιο από bluegalazios — 11 Μαρτίου, 2010 @ 1:41 πμ
..καθε φορα που τρεχουμε το πειραμα. Οποτε αν εχω προαποφασισει το πληθος αυτων που θα ελεγχθουν δεν επηρεαζω τις πιθανοτητες επιλογης για τον καθε εναν…
Μου αρέσει!Μου αρέσει!
Σχόλιο από bluegalazios — 11 Μαρτίου, 2010 @ 1:55 πμ
Αυτό που είναι προκαθορισμένο είναι η πιθανότητα με την οποία ο καθένας θα ελεγχθεί.
Σε κάθε τρέξιμο του πειράματος όμως το πλήθος αυτών που ελέγχονται μπορεί να διαφέρει. Π.χ. μπορεί να μην ελεγχθεί κανείς. Αυτό το ενδεχόμενο έχει θετική πιθανότητα και ίση με , όπου
, όπου  το πλήθος όλων των ατόμων και
το πλήθος όλων των ατόμων και  η πιθανότητα να ελεγχθεί ο καθένας από αυτούς.
η πιθανότητα να ελεγχθεί ο καθένας από αυτούς.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 11 Μαρτίου, 2010 @ 2:21 πμ
Μια στιγμη…αρα το ζητουμενο ειναι ενας τυχαιος αριθμος τελικων επιλαχθεντων,οι οποιοι θα εχουν επιλεγει ο καθενας με τυχαιο τροπο με ΕΝΑ τρεξιμο του πειραματος…ετσι δεν ειναι?? (θα ηταν διασκεδαστικο οι απαντησεις και λυσεις του καθενος να βαθμολογουνται..αλλωστε καθηγητης δεν ειστε?)
Μου αρέσει!Μου αρέσει!
Σχόλιο από bluegalazios — 11 Μαρτίου, 2010 @ 11:32 μμ
Αν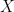 είναι η κατανομή του σχόλιου 16, η
είναι η κατανομή του σχόλιου 16, η 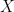 ακολουθεί την διωνυμική με παραμέτρους
ακολουθεί την διωνυμική με παραμέτρους 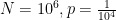 . Αν
. Αν  τότε μπορούμε να παράγουμε το δείγμα ως εξής: Βάζουμε σε ένα κουτί όλες τις
τότε μπορούμε να παράγουμε το δείγμα ως εξής: Βάζουμε σε ένα κουτί όλες τις  -άδες των αριθμών
-άδες των αριθμών 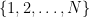 που είναι
που είναι 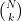 το πλήθος και επιλέγουμε τυχαία μια.
το πλήθος και επιλέγουμε τυχαία μια.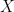 . Θέλουμε να επιλέξουμε ένα αριθμό
. Θέλουμε να επιλέξουμε ένα αριθμό 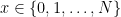 έτσι ώστε να ισχύει
έτσι ώστε να ισχύει  . Βάζουμε σε ένα κουτί τους
. Βάζουμε σε ένα κουτί τους 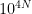 αριθμούς
αριθμούς  όπου ο αριθμός
όπου ο αριθμός  εμφανίζεται
εμφανίζεται 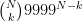 φορές για
φορές για 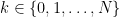 και επιλέγουμε τυχαία ένα.
και επιλέγουμε τυχαία ένα. άρρητο;
άρρητο;
Τώρα πως θα επιλέξουμε την τιμη της
Εκεί που λέω να βάλουμε σε κουτί αριθμούς και να επιλέξουμε ένα θα χρειαστούμε τη βοήθεια υπολογιστή αν επιτρέπετε.
Αν η λύση είναι σωστή, υπάρχει άλλος τρόπος να λυθεί αυτό το πρόβλημα για
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 8 Απριλίου, 2010 @ 11:20 μμ
Σκοπός αυτού του προβλήματος είναι να προτείνουμε μια λύση πρακτική, δηλ. γρήγορη, και να έχουμε και μια τεκμηριωμένη εκτίμηση του πόσο γρήγορη.
Η τυχαία μας επιλογή λοιπόν θα γίνει σε δύο στάδια.
(α) Επιλέγουμε το πόσους θα ελέγξουμε, έστω , παίρνουμε δηλ. ένα δείγμα της τυχαίας μεταβλητής
, παίρνουμε δηλ. ένα δείγμα της τυχαίας μεταβλητής 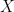 του σχολίου 16, και η οποία όντως ακολουθεί διωνυμική κατανομή με τις παραμέτρους που αναφέρονται στο σχόλιο 21, και
του σχολίου 16, και η οποία όντως ακολουθεί διωνυμική κατανομή με τις παραμέτρους που αναφέρονται στο σχόλιο 21, και
(β) Επιλέγουμε άτομα από τα
άτομα από τα  με τέτοιο τρόπο ώστε κάθε υποσύνολο μεγέθους
με τέτοιο τρόπο ώστε κάθε υποσύνολο μεγέθους  από τα
από τα 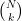 δυνατά υποσύνολα να έχει την ίδια πιθανότητα να επιλεγεί.
δυνατά υποσύνολα να έχει την ίδια πιθανότητα να επιλεγεί.
Το ότι η επιλογή που γίνεται κατ’ αυτόν τον τρόπο παράγει το ίδιο αποτέλεσμα (δηλ. την ίδια κατανομή αποτελεσμάτων) με το να ρίξουμε ένα ζάρι φορές είναι αυτό που λύνει το πρόβλημα, αρκεί βεβαίως να καταφέρουμε να υλοποιήσουμε τα στάδια (α) και (β) σε χρόνο αρκετά μικρότερο του
φορές είναι αυτό που λύνει το πρόβλημα, αρκεί βεβαίως να καταφέρουμε να υλοποιήσουμε τα στάδια (α) και (β) σε χρόνο αρκετά μικρότερο του  (που είναι φανερό ότι είναι ο χρόνος που απαιτείται για να ρίξουμε το ζάρι για τον καθένα). Και το ότι τα (α,β) παράγουν την ίδια κατανομή με τη ρίψη του ζαριού
(που είναι φανερό ότι είναι ο χρόνος που απαιτείται για να ρίξουμε το ζάρι για τον καθένα). Και το ότι τα (α,β) παράγουν την ίδια κατανομή με τη ρίψη του ζαριού  φορές θέλει φυσικά απόδειξη αλλά αυτή δεν είναι κάτι το ιδιαίτερο.
φορές θέλει φυσικά απόδειξη αλλά αυτή δεν είναι κάτι το ιδιαίτερο.
Όμως απομένει ακόμη πολύ λεπτομέρεια για την υλοποίηση των (α) και (β) που θέλει ξεκαθάρισμα.
Το πιο εύκολο είναι η υλοποίηση του (β). Ας υποθέσουμε κατ’ αρχήν ότι ο αριθμός (το δείγμα της
(το δείγμα της 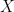 , το πλήθος αυτών που θα ελεγχθούν) είναι μικρός, π.χ. μέχρι
, το πλήθος αυτών που θα ελεγχθούν) είναι μικρός, π.χ. μέχρι  (μέχρι 10 φορές δηλ. τη μέση τιμή του). Τότε μπορούμε να επιλέξουμε αυτούς που θα ελεγχθούν ως εξής: επιλέγουμε ένα τυχαίο αριθμό από τους
(μέχρι 10 φορές δηλ. τη μέση τιμή του). Τότε μπορούμε να επιλέξουμε αυτούς που θα ελεγχθούν ως εξής: επιλέγουμε ένα τυχαίο αριθμό από τους  ως τον πρώτο που θα ελεγχθεί, κατόπιν ομοίως τον 2ο κλπ. Αν προκύψει κάποιος που έχει ήδη επιλεγεί τότε απλά ξαναδοκιμάζουμε. Η διαίσθησή μας μας λέει ότι, αφού ο
ως τον πρώτο που θα ελεγχθεί, κατόπιν ομοίως τον 2ο κλπ. Αν προκύψει κάποιος που έχει ήδη επιλεγεί τότε απλά ξαναδοκιμάζουμε. Η διαίσθησή μας μας λέει ότι, αφού ο  είναι πολύ μικρότερος από τον
είναι πολύ μικρότερος από τον  τότε σπανίως θα χρειαστεί να ξαναεπιλέξουμε.
τότε σπανίως θα χρειαστεί να ξαναεπιλέξουμε.
Ας αφήσουμε για λίγο το στάδιο (α) κατά μέρος και ας δούμε πόσο χρόνο παίρνει το (β). Συγκεκριμένα, ποιος είναι ο μέσος χρόνος που κοστίζει το (β); Πόσες τυχαίες επιλογές θα χρειαστεί να κάνουμε (και πάλι κατά μέσο όρο); Δε χρειαζόμαστε ακριβείς ποσότητες. Εύχρηστα άνω φράγματα είναι μια χαρά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Απριλίου, 2010 @ 5:03 μμ