Ας είναι ένας πεπερασμένος μετρικός χώρος. Αυτό σημαίνει ότι για κάθε δύο σημεία
έχει οριστεί μια θετική «απόσταση»
ανάμεσά τους, και οι αποστάσεις αυτές πληρούν την τριγωνική ανισότητα
, για κάθε
.
Κατασκευάστε μια 1-1 συνάρτηση τέτοια ώστε για κάθε
να ισχύει
όπου , για
.
Αρκεί να ορίσουμε f(x)=(d(x,x_1),\ldots , d(x,x_n))
Από την τριγωνική ανισότητα προκύπτει άμεσα ότι η συνάρτηση πληροί το ζητούμενο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexandrosg — 13 Δεκεμβρίου, 2009 @ 11:54 μμ
Πολύ σωστά.
Μπορείτε να κάνετε το ίδιο στον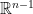 αντί για τον
αντί για τον 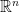 ;
;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 15 Δεκεμβρίου, 2009 @ 12:14 πμ
Μπορούμε να ορίσουμε $ f(x)=(d(x,x_2),\ldots , d(x,x_n))$ (η φυσικά να ορίσουμε να παραλείπεται η απόσταση προς κάποιο άλλο από τα στοιχεία του συνόλου).
Μου αρέσει!Μου αρέσει!
Σχόλιο από alexandrosg — 16 Δεκεμβρίου, 2009 @ 3:08 μμ
Πολύ σωστά.
Μπορεί κανείς να δείξει ένα τέτοιο θέωρημα αν η μετρική στην εικόνα είναι η και όχι η
και όχι η 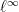 ;
;
Υπάρχει δηλ. 1-1 απεικόνιση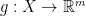 , με
, με  ενδεχομένως πολύ μεγαλύτερο από το
ενδεχομένως πολύ μεγαλύτερο από το  , ώστε να ισχύει
, ώστε να ισχύει 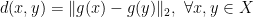 ;
;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 17 Δεκεμβρίου, 2009 @ 4:33 μμ