Είναι εύκολο να δει κανείς (γιατί;) ότι οποιοδήποτε πολυώνυμο σε μια μεταβλητή με πραγματικούς συντελεστές είναι μη αρνητικό για κάθε
γράφεται αναγκαστικά σα άθροισμα τετραγώνων πολυωνύμων
, με
.
Άρα το να γράφεται ένα πολυώνυμο μιας μεταβλητής σα άθροισμα τετραγώνων είναι ισοδύναμο με το να είναι πάντα μη αρνητικό.
Έστω . Δείξτε ότι το
είναι πάντα μη αρνητικό αλλά δε μπορεί να γραφεί σα άθροισμα τετραγώνων πολυωνύμων σε
. Άρα η παραπάνω ισοδυναμία δεν ισχύει παρά μόνο για πολυώνυμα μιας μεταβλητής.
Η συναρτηση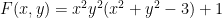 ειναι θετικη εαν και μονο εαν
ειναι θετικη εαν και μονο εαν  για καθε ζευγαρι απο
για καθε ζευγαρι απο  τα οποια ειναι μη μηδενικα. Ισοδυναμα για καθε
τα οποια ειναι μη μηδενικα. Ισοδυναμα για καθε  ισχυει:
ισχυει:  . Αλλα
. Αλλα ![a+b+\frac1{ab}=3(\frac{a+b+\frac1{ab}}{3})\geq 3\sqrt[3]{ab\frac1{ab}}=3](https://s0.wp.com/latex.php?latex=a%2Bb%2B%5Cfrac1%7Bab%7D%3D3%28%5Cfrac%7Ba%2Bb%2B%5Cfrac1%7Bab%7D%7D%7B3%7D%29%5Cgeq+3%5Csqrt%5B3%5D%7Bab%5Cfrac1%7Bab%7D%7D%3D3&bg=ffffff&fg=000000&s=0&c=20201002) χρησιμοποιωντας την ανισωση αριθμητικου-γεωμετρικου μεσου. Αρα η συναρτηση μας ειναι μη αρνητικη. Παραμενει ο ισχυρισμος με τα πολυωνυμα.
χρησιμοποιωντας την ανισωση αριθμητικου-γεωμετρικου μεσου. Αρα η συναρτηση μας ειναι μη αρνητικη. Παραμενει ο ισχυρισμος με τα πολυωνυμα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από nikos3223 — 27 Νοεμβρίου, 2009 @ 9:23 μμ
Μέχρι εδώ πολύ καλά.
Υποθέστε ότι γράφεται σαν άθροισμα τετραγώνων πολυωνύμων και καταλήξετε σε άτοπο. Πείτε επίσης γιατί ισχύει στη μια μεταβλητή ότι γράφεται σαν άθροισμα τετραγώνων.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Νοεμβρίου, 2009 @ 10:33 μμ
Υποδειξη: Όσον αφορά τα πολυώνυμα μιας μεταβλητής, κοιτάξτε τις ρίζες τους στο μιγαδικό επίπεδο και ομαδοποιείστε τις κατάλληλα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Ιανουαρίου, 2010 @ 9:12 πμ
Για το πρώτο ερώτημα:
Αν και
και  τότε
τότε 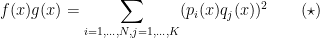
Έστω![f(x)\in \mathbb{R}[x]](https://s0.wp.com/latex.php?latex=f%28x%29%5Cin+%5Cmathbb%7BR%7D%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) με
με 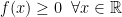 .Από το
.Από το  μπορούμε να υποθέσουμε ότι είναι μονικό.
μπορούμε να υποθέσουμε ότι είναι μονικό.
Έστω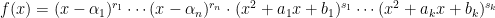 η ανάλυση του σε γινόμενο αναγωγων πολυωνύμων επί του
η ανάλυση του σε γινόμενο αναγωγων πολυωνύμων επί του  . Διακρίνουμε δύο περιπτώσεις:
. Διακρίνουμε δύο περιπτώσεις:
1)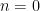
Σε αυτή τη περίπτωση ( )
)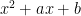 είναι ανάγωγο επί του
είναι ανάγωγο επί του  τότε
τότε
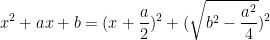 οπότε το αποτέλεσμα έπεται από το
οπότε το αποτέλεσμα έπεται από το  .
.
αρκεί να παρατηρήσουμε ότι αν το
2)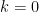
Σε αυτή τη περίπτωση (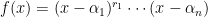 ) θα δείξουμε ότι οι
) θα δείξουμε ότι οι 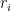 είναι άρτιοι. Αν υποθέσουμε ότι κάποιος
είναι άρτιοι. Αν υποθέσουμε ότι κάποιος 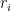 ήταν περιττός τότε το πολυώνυμο
ήταν περιττός τότε το πολυώνυμο  θα ήταν θετικό στο
θα ήταν θετικό στο 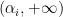 και αρνητικό στο
και αρνητικό στο  άρα θα είχε ρίζα το
άρα θα είχε ρίζα το  . Άτοπο.
. Άτοπο.
Από το ( ) και τα 1) και 2) παίρνουμε το αποτέλεσμα.
) και τα 1) και 2) παίρνουμε το αποτέλεσμα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Pambos — 16 Μαρτίου, 2012 @ 3:47 μμ
Έχω κάποια τυπογραφικά.
Στη περίπτωση 1) το ριζικό πρέπει να είναι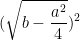
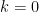 άρα
άρα 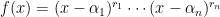
και η περίπτωση 2) είναι
Μου αρέσει!Μου αρέσει!
Σχόλιο από Pambos — 16 Μαρτίου, 2012 @ 4:15 μμ
Σωστά, αν και στην περίπτωση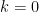 που αναφέρεις παραπάνω πρέπει να πεις ότι στην περίπτωση που ο εκθέτης ενός παράγοντα είναι περιττός τότε αλλάζει πρόσημο στην γειτονιά της ρίζας του ενώ (για κατάλληλα μικρή γειτονιά) κανείς άλλος από τους παράγοντες δεν αλλάζει πρόσημα, άρα υπάρχει αντίφαση.
που αναφέρεις παραπάνω πρέπει να πεις ότι στην περίπτωση που ο εκθέτης ενός παράγοντα είναι περιττός τότε αλλάζει πρόσημο στην γειτονιά της ρίζας του ενώ (για κατάλληλα μικρή γειτονιά) κανείς άλλος από τους παράγοντες δεν αλλάζει πρόσημα, άρα υπάρχει αντίφαση.
Υπάρχει και μια κάπως πιο κομψή λύση αν κανείς κάνει την παρατήρηση ότι σε κάθε πραγματικό πολυώνυμο οι μιγαδικές του ρίζες που δεν είναι πραγματικοί αριθμοί είναι πάντα ζευγαρωμένες: αν είναι ρίζα τότε και
είναι ρίζα τότε και 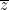 είναι ρίζα.
είναι ρίζα.
Τι γίνεται στις δύο μεταβλητές;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 16 Μαρτίου, 2012 @ 6:08 μμ
Πράγματι είναι λάθος αυτό που έγραψα στη περίπτωση 2. Το σωστό είναι
«Αν υποθέσουμε ότι κάποιος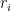 ήταν περιττός τότε το πολυώνυμο
ήταν περιττός τότε το πολυώνυμο  θα ήταν θετικό στο
θα ήταν θετικό στο 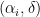 και αρνητικό στο
και αρνητικό στο  για κατάλληλο
για κατάλληλο 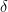 μικρό άρα θα είχε ρίζα το
μικρό άρα θα είχε ρίζα το  . Άτοπο.»
. Άτοπο.»
Τώρα για το πολυώνυμο υποθέτουμε για άτοπο ότι
υποθέτουμε για άτοπο ότι  .
. έπεται ότι
έπεται ότι  με
με  και
και 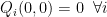 .
.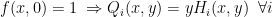 και από την
και από την  παίρνουμε
παίρνουμε  .
.
Αφού
Τώρα επειδή
Τέλος για παίρνουμε
παίρνουμε  .
. μιας μεταβλητής θα έχουν βαθμό
μιας μεταβλητής θα έχουν βαθμό  και θα έχουν για ρίζες τους
και θα έχουν για ρίζες τους  άρα τα πολυώνυμα
άρα τα πολυώνυμα 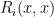 θα έχουν βαθμό
θα έχουν βαθμό 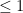 και
και 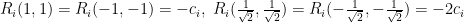 . Άτοπο.
. Άτοπο.
Τα πολυώνυμα
Μου αρέσει!Μου αρέσει!
Σχόλιο από Pambos — 16 Μαρτίου, 2012 @ 11:02 μμ
?
Μου αρέσει!Μου αρέσει!
Σχόλιο από Pambos — 1 Απριλίου, 2012 @ 2:07 μμ
Sorry, έχω μείνει λίγο πίσω. Θα γράψω σύντομα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 1 Απριλίου, 2012 @ 6:20 μμ
Νομίζω η παραγοντοποίησή σου είναι λάθος: εδώ
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 3 Απριλίου, 2012 @ 11:06 πμ
Σωστά η παραγοντοποίησή μου είναι λάθος. Η σωστή παραγοντοποίηση είναι
Η λύση όμως νομίζω σώζεται αν αλλάξουμε τη τελευταία παράγραφο σε: μιας μεταβλητής θα έχουν βαθμό
μιας μεταβλητής θα έχουν βαθμό  και θα έχουν για ρίζες τους
και θα έχουν για ρίζες τους  άρα τα πολυώνυμα
άρα τα πολυώνυμα 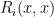 θα έχουν βαθμό
θα έχουν βαθμό 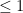 και
και  . Άτοπο.
. Άτοπο.
Τα πολυώνυμα
Μου αρέσει!Μου αρέσει!
Σχόλιο από Pambos — 3 Απριλίου, 2012 @ 3:24 μμ
Σωστό.
Αλλά πρέπει να τονιστεί εδώ ότι τα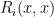 είναι πραγματικοί αριθμοί όταν
είναι πραγματικοί αριθμοί όταν  είναι πραγματικός ή φανταστικός αριθμός, όπως προκύπτει από τη σχέση
είναι πραγματικός ή φανταστικός αριθμός, όπως προκύπτει από τη σχέση 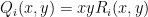 που έχεις πιο πάνω. Άρα το
που έχεις πιο πάνω. Άρα το  είναι άθροισμα τετραγώνων πραγματικών αριθμών και άρα οι ρίζες του
είναι άθροισμα τετραγώνων πραγματικών αριθμών και άρα οι ρίζες του  είναι και ρίζες κάθε τετραγώνου χωριστά.
είναι και ρίζες κάθε τετραγώνου χωριστά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Απριλίου, 2012 @ 7:12 πμ