Τρείς φίλοι ξεκινούν έχοντας ένα (ακέραιο, θετικό) χρηματικό ποσό ο καθένας.
Σε κάθε βήμα δύο από αυτούς μπορούν να τροποποιούν τα ποσά που έχουν ως εξής:
αν είναι τα δύο ποσά τότε αυτός που έχει τα περισσότερα δίνει στον άλλο όσα έχει ο άλλος. Τα δύο ποσά γίνονται δηλ.
και
.
Δείξτε ότι είναι πάντα δυνατό να κάνουν αυτές τις αλλαγές με τέτοιο τρόπο ώστε κάποιος από τους τρεις να καταλήξει χωρίς καθόλου χρήματα.
Οι ανταλλαγές γίνονται σε τυχαία σειρά ή πχ πρώτα ο Α με τον Β, μετά ο Β με τον Γ, μετά ο Γ με τον Α κοκ?
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 21 Οκτωβρίου, 2009 @ 2:06 μμ
Όπως αυτοί θέλουν ώστε να πετύχουν το σκοπό τους.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 21 Οκτωβρίου, 2009 @ 2:32 μμ
Υπόδειξη:
Θεωρείστε δύο άτομα από τα τρία μόνο και υποθέστε ότι ο ένας έχει περιττό ποσό και ο άλλος άρτιο. Δείξτε ότι αυτός που έχει το άρτιο ποσό μπορεί να δώσει στον άλλο τα μισά. (Αφήστε τον τρίτο απ’ έξω για να το δείξετε. Δε χρειάζεται να τον ανακατέψετε.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Οκτωβρίου, 2009 @ 10:59 πμ
Μα πώς; Aς πούμε ο ένας έχει 17 και ο άλλος 4. Πώς μπορεί ο άρτιος να δώσει τα μισά στον περιττό αφού είναι μικρότερος; δεν επιτρεπεται από τους κανόνες.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 24 Οκτωβρίου, 2009 @ 10:09 πμ
Μπορούμε να φανταστούμε τους αριθμούς σαν σημεία επάνω στον άξονα των φυσικών αριθμών τα οποία κινούνται. Έστω Α<=Β<=Γ. Αν είναι όλοι τους άρτιοι τότε μπορώ να παράγω κάθε άρτιο με τις δοσοληψίες που γίνονται ανάμεσα στον Α και τον Γ (οι δοσοληψίες με άρτιους πάντα σε άρτια ποσά με αφήνουν). Είναι σα να έχω ένα διάστημα και συστέλλω τα άκρα του (από αριστερά και από δεξιά) κατά το ίδιο ποσό, κι έχω κι ένα σημείο μέσα στο διάστημα που ορίζουν τα άκρα. Κάποτε κάποιο άκρο θα συμπέσει με το σημείο. Για περιττούς δεν έχω σκεφτεί, δεν διαιρούνται ακριβώς…
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 24 Οκτωβρίου, 2009 @ 10:18 πμ
Αυτά που λες για τους άρτιους δεν είναι σωστά αιτιολογημένα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 24 Οκτωβρίου, 2009 @ 1:56 μμ
Υπόδειξη: Για να δείξετε αυτό που ζητάει η προηγούμενη υπόδειξη παρατηρείστε ότι αν δύο άτομα (θυμηθείτε ότι αγνοούμε τον τρίτο) έχουν άρτιο και περιττό ποσό τότε μετά από ένα γύρο (α) πάλι θα έχουμε ένα άρτιο και ένα περιττό και (β) κάθε τέτοια κατάσταση μπορεί να έχει προέλθει από μόνο μια άλλη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 26 Οκτωβρίου, 2009 @ 12:50 μμ
Έστω ένας από αυτούς περιττός και ένας άρτιος, τότε στις μεταξύ τους δοσοληψίες, κάποια στιγμή ο ένας από τους δύο θα φθάσει να έχει ποσό ίσο με τη μονάδα, ενώ ο άλλος θα έχει άρτιο ποσό. Σταματάνε εκέι τις δοσοληψίες.
Εάν ο τρίτος είναι περιττός, τότε αυτός που έχει άρτιο ποσό ξεκινά μαζί του δοσοληψίες μέχρι κάποιος να έχει μονάδα. Μετά οι δύο φίλοι που έχουν μονάδες κάνουν μία τελευταία δοσοληψία μεταξύ τους.
Εάν ο τρίτος είναι άρτιος τότε κάνει μία δοσοληψία με αυτόν που έχει μονάδα, οπότε ο τελευταίος αποκτά 2 μονάδες και ο άλλος περιττό. Οπότε αυτός με το περιττό ποσό κάνει δοσοληψία με τον άρτιο μέχρι κάποιος να αποκτήσει ποσό μονάδα. Στη συνέχεια κάνουν άλλη μία δοσοληψία μέχρι να αποκτήσει αυτός που έχει μονάδα, 2 μονάδες, και τελικά αυτοί που έχουν 2 μονάδες κάνουν μία τελευταία δοσοληψία.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 27 Οκτωβρίου, 2009 @ 11:07 μμ
pebox, λες:
Έστω ένας από αυτούς περιττός και ένας άρτιος, τότε στις μεταξύ τους δοσοληψίες, κάποια στιγμή ο ένας από τους δύο θα φθάσει να έχει ποσό ίσο με τη μονάδα, ενώ ο άλλος θα έχει άρτιο ποσό. Σταματάνε εκέι τις δοσοληψίες.
Γιατί;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Οκτωβρίου, 2009 @ 11:16 μμ
ναι πιο σωστά ίσως θα ήταν να έλεγα σταματάνε εκεί τις δοσοληψίες και κοιτάνε τί ποσό έχει ο τρίτος, εάν έχει άρτιο ποσό μονάδων πέφτουν στη 2η περ. που έγραψα, εάν περιττό στην 1η.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 27 Οκτωβρίου, 2009 @ 11:30 μμ
Γιατί θα φτάσουν να έχει κάποιος μονάδα;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Οκτωβρίου, 2009 @ 11:32 μμ
ναι σωστά δεν φτάνουν πάντα. δεν δουλεύει. νομιζω όμως ότι πάντα ανταλλάζουν χρήματα εάν επαναλλάβουν ικανές φορές τις δοσοληψίες
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 27 Οκτωβρίου, 2009 @ 11:57 μμ
Υποθέτουμε ότι ισχύει η υπόδειξη. Δηλαδή ότι αν ο ένας έχει (ευρώ) και ο άλλος
(ευρώ) και ο άλλος  με
με  περιττός τότε μετά από κάποιες δοσοληψίες θα έχουν
περιττός τότε μετά από κάποιες δοσοληψίες θα έχουν 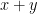 ,
, 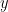 χωρίς να λαμβάνουμε υπόψη τη σειρά. Άρα αν έχουν
χωρίς να λαμβάνουμε υπόψη τη σειρά. Άρα αν έχουν  με
με  περιττό τότε μετά από κάποιες δοσοληψίες θα έχουν
περιττό τότε μετά από κάποιες δοσοληψίες θα έχουν 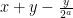 ,
,  με
με  περιττό.
περιττό. με
με 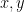 περιττούς. Τότε μπορούμε να υποθέσουμε ότι
περιττούς. Τότε μπορούμε να υποθέσουμε ότι 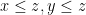 ( αν δεν ισχύει κάνουν δοσοληψίες οι
( αν δεν ισχύει κάνουν δοσοληψίες οι 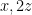 μέχρι να ελαχιστοποιηθεί ο περιττός και μετά ο
μέχρι να ελαχιστοποιηθεί ο περιττός και μετά ο 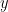 με τον άρτιο μέχρι να ελαχιστοποιηθεί ο περιττός). Υποθέτουμε ακόμη ότι
με τον άρτιο μέχρι να ελαχιστοποιηθεί ο περιττός). Υποθέτουμε ακόμη ότι 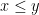 Αν
Αν  κάνουν μια τελευταία δοσοληψία. Αν
κάνουν μια τελευταία δοσοληψία. Αν 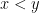 τότε μετά από μια δοσοληψία θα έχουν
τότε μετά από μια δοσοληψία θα έχουν  . Μετά από κάποιες δοσοληψίες θα έχουν
. Μετά από κάποιες δοσοληψίες θα έχουν  (
( άρτιος) και μετά από κάποιες δοσοληψίες θα έχουν
άρτιος) και μετά από κάποιες δοσοληψίες θα έχουν 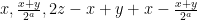 όπου ο
όπου ο 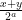 είναι περιττός. Επειδή
είναι περιττός. Επειδή 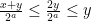 με ισότητα αν
με ισότητα αν  συνεχίζοντας με αυτό το τρόπο οι περιττοί θα ελαττώνονται συνεχώς μέχρι τα τρία άτομα να έχουν ποσά
συνεχίζοντας με αυτό το τρόπο οι περιττοί θα ελαττώνονται συνεχώς μέχρι τα τρία άτομα να έχουν ποσά 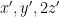 με
με  (περιττός) οπότε κάνουν μία τελευταία δοσοληψία.
(περιττός) οπότε κάνουν μία τελευταία δοσοληψία. με
με  περιττό μπορούμε να υποθέσουμε ότι
περιττό μπορούμε να υποθέσουμε ότι  (αλλιώς κάνουν δοσοληψίες πρώτα οι
(αλλιώς κάνουν δοσοληψίες πρώτα οι  και μετά ο περιττός με τον
και μετά ο περιττός με τον 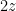 σταματώντας σε κάθε περίπτωση όταν ελαχιστοποιηθεί ο περιττός). Μετά από μια δοσοληψία θα έχουν
σταματώντας σε κάθε περίπτωση όταν ελαχιστοποιηθεί ο περιττός). Μετά από μια δοσοληψία θα έχουν  , μετά από κάποιες δοσοληψίες θα έχουν
, μετά από κάποιες δοσοληψίες θα έχουν 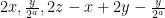 με
με  περιττό και μετά από κάποιες δοσοληψίες θα έχουν
περιττό και μετά από κάποιες δοσοληψίες θα έχουν 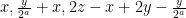 . Αφού
. Αφού  με ισότητα αν
με ισότητα αν  συνεχίζοντας με αυτό το τρόπο κάποια στιγμή θα έχουν
συνεχίζοντας με αυτό το τρόπο κάποια στιγμή θα έχουν 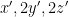 με
με 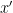 περιττό και
περιττό και 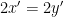 οπότε κάνουν μια δοσοληψία ο πρώτος με τον τρίτο και μετά ο πρώτος με τον δεύτερο.
οπότε κάνουν μια δοσοληψία ο πρώτος με τον τρίτο και μετά ο πρώτος με τον δεύτερο.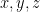 με
με 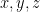 άρτιους τότε αν
άρτιους τότε αν  είναι ο μ.κ.δ. των
είναι ο μ.κ.δ. των 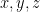 και
και  φυσικός έτσι ώστε ο
φυσικός έτσι ώστε ο 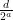 είναι περιττός τότε η τριάδα
είναι περιττός τότε η τριάδα 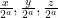 είναι σε κάποια από τις προηγούμενες περιπτώσεις. Ακολουθούμε τότε τον αλγόριθμο της περίπτωσης που ανήκει η
είναι σε κάποια από τις προηγούμενες περιπτώσεις. Ακολουθούμε τότε τον αλγόριθμο της περίπτωσης που ανήκει η 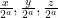 με την αντιστοιχία
με την αντιστοιχία  .
.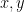 είναι ίσος με τον μ.κ.δ. των
είναι ίσος με τον μ.κ.δ. των  κ.ο.κ.
κ.ο.κ. περιττός
περιττός 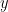 άρτιος) μπορούμε να ορίσουμε το σύνολο
άρτιος) μπορούμε να ορίσουμε το σύνολο 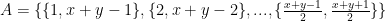 και την απεικόνιση
και την απεικόνιση  με
με 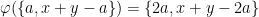 για
για  . Τότε η φ είναι 1-1 και επί (
. Τότε η φ είναι 1-1 και επί ( 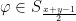 ) και μετά από κάθε δοσοληψία το αποτέλεσμα είναι η εικόνα των ποσών που έχουν τα 2 άτομα μέσω της φ.
) και μετά από κάθε δοσοληψία το αποτέλεσμα είναι η εικόνα των ποσών που έχουν τα 2 άτομα μέσω της φ.
Έχουμε τις περιπτώσεις:
(Εκεί που δε θα γράφω ποιοι κάνουν τις δοσοληψίες θα προκύπτει από το αποτέλεσμα)
1)Τα τρία άτομα έχουν
2)Αν έχουν ποσά
3)Αν έχουν και οι τρεις περιττό ποσό με μια δοσοληψία αναγόμαστε στη προηγούμενη περίπτωση.
4)Αν τώρα έχουν
Το τελευταίο ισχύει γιατί σε αυτή τη περίπτωση ο μ.κ.δ. των
Για να δούμε ότι ισχύει η υπόδειξη (αν
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 20 Μαρτίου, 2010 @ 12:22 πμ
pamp0s:
Είμαι λίγο μπερδεμένος με τη λύση που προτείνεις. Για παράδειγμα, γράφεις στο τέλος της 1ης παραγράφου:
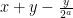 αλλά μάλλον εννοείς
αλλά μάλλον εννοείς 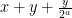 .
.
Επίσης μιλάς στο 1) για την ελαχιστοποίηση του περιττού αλλά δε βλέπω πώς.
Αν μπορείς ξαναγράψε το πιο αναλυτικά. Οι πολλές περιπτώσεις κάνουν μια τέτοια απόδειξη κάπως δυσανάγνωστη. Αυτό μπορεί φυσικά να είναι αναπόφευκτο, αλλά αξίζει να βρίσκει κανείς ένα κομψό τρόπο να τη διατυπώσει.
(Συγγνώμη για την καθυστερημένη απάντηση αλλά έλειπα κάποιες μέρες.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 22 Μαρτίου, 2010 @ 3:40 μμ
Καλησπέρα.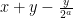 νομίζω είναι σωστό. Σε κάθε δοσοληψία το άθροισμα των ποσών μετά την δοσοληψία είναι ίσο με το άθροισμα των ποσών πριν τη δοσοληψία. Αυτό που θέλω να πω εκεί είναι ότι αν ο ένας έχει περιττό ποσό και ο άλλος άρτιο και υποθέσουμε ότι αυτός που έχει το άρτιο ποσό μπορεί να δώσει στον άλλο τα μισά τότε μπορεί να το κάνει συνεχώς μέχρι να του μείνει περιττό ποσό. Για παράδειγμα αν ο ένας έχει 21 και ο άλλος 560 (
νομίζω είναι σωστό. Σε κάθε δοσοληψία το άθροισμα των ποσών μετά την δοσοληψία είναι ίσο με το άθροισμα των ποσών πριν τη δοσοληψία. Αυτό που θέλω να πω εκεί είναι ότι αν ο ένας έχει περιττό ποσό και ο άλλος άρτιο και υποθέσουμε ότι αυτός που έχει το άρτιο ποσό μπορεί να δώσει στον άλλο τα μισά τότε μπορεί να το κάνει συνεχώς μέχρι να του μείνει περιττό ποσό. Για παράδειγμα αν ο ένας έχει 21 και ο άλλος 560 ( ) μετά από κάποιες δοσοληψίες μπορεί ο δεύτερος να δώσει τα 280 (
) μετά από κάποιες δοσοληψίες μπορεί ο δεύτερος να δώσει τα 280 (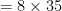 ) και να του μείνουν 280. Κάνοντας το ίδιο μπορεί μετά από κάποιες δοσοληψίες να μείνει με 35 οπότε ο πρώτος θα έχει (αναγκαστικά) 546 (
) και να του μείνουν 280. Κάνοντας το ίδιο μπορεί μετά από κάποιες δοσοληψίες να μείνει με 35 οπότε ο πρώτος θα έχει (αναγκαστικά) 546 ( ).
).
Έχετε δίκαιο στο ότι είναι δυσανάγνωστη η λύση αλλά δυστυχώς είναι ο καλύτερος τρόπος που μπορούσα να την παρουσιάσω. Θα εφαρμόσω όμως τον «αλγόριθμο» της περίπτωσης 1) σε συγκεκριμένο παράδειγμα και ελπίζω με αυτό να γίνω πιο κατανοητός.
Πρώτα όμως στο τέλος της πρώτης παραγράφου το
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 23 Μαρτίου, 2010 @ 10:35 μμ
Τώρα να εφαρμόσω την περίπτωση 1) σε συγκεκριμένο παράδειγμα.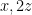 μέχρι να ελαχιστοποιηθεί ο περιττός …») εννοώ να κάνουν το εξής:
μέχρι να ελαχιστοποιηθεί ο περιττός …») εννοώ να κάνουν το εξής: . Τα περιττά ποσά είναι
. Τα περιττά ποσά είναι 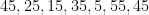 με ελάχιστο το 5. Οπότε ξαναρχίζουν τις δοσοληψίες και σταματούν όταν θα έχουν ποσά 5,60. Άρα τα ποσά των τριών έγιναν 5,21,60. Κάνουν το ίδιο οι 21,60 και μετά από δύο δοσοληψίες έχουν 3,78. Άρα τα ποσά των τριών γίνονται 5,3,78 και ισχύει
με ελάχιστο το 5. Οπότε ξαναρχίζουν τις δοσοληψίες και σταματούν όταν θα έχουν ποσά 5,60. Άρα τα ποσά των τριών έγιναν 5,21,60. Κάνουν το ίδιο οι 21,60 και μετά από δύο δοσοληψίες έχουν 3,78. Άρα τα ποσά των τριών γίνονται 5,3,78 και ισχύει  (Η ανισότητες θα ισχύουν στη γενική περίπτωση λόγο της πρώτης παραγράφου του σχόλιου 13).
(Η ανισότητες θα ισχύουν στη γενική περίπτωση λόγο της πρώτης παραγράφου του σχόλιου 13).
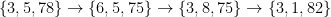 .
.
Έστω ότι έχουν τα ποσά 45,21,20. Εκεί που λέω για ελαχιστοποίηση του περιττού (» αν δεν ισχύει κάνουν δοσοληψίες οι
Αρχίζουν τις δοσοληψίες οι 45, 20 μέχρι να καταλήξουν με ποσά 45, 20 (αυτό γίνετε λόγο της τελευταίας παραγράφου του σχολίου 13). Σε κάθε δοσοληψία σημειώνουν το περιττό ποσό και βρίσκουν το ελάχιστο. Μετά ξαναρχίζουν τις δοσοληψίες μέχρι να πετύχουν αυτό το ελάχιστο περιττό ποσό. Στο παράδειγμα πρώτα κάνουν τις εξής δοσοληψίες
Μετά διατάσσουμε τα περιττά ποσά και έχουμε τα 3,5,78.
Ακολουθώντας τον αλγόριθμο της περίπτωσης 1 κάνουμε τις εξής δοσοληψίες:
Τα διατάσσουμε σε {1,3,82} και συνεχίζουμε με τον ίδιο τρόπο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pamp0s — 23 Μαρτίου, 2010 @ 11:14 μμ
pamp0s:
(Συγγνώμη για την καθυστερημένη απάντηση αλλά αυτές τις μέρες ταξιδεύω.)
Νομίζω κατάλαβα τη λύση σου. Ας την ανακεφαλαιώσω λίγο για να ξεκαθαρίσω ορισμένα πράγματα. Αναφέρομαι λοιπόν στο σχόλιο 13.
Στην αρχή του σχολίου η ποσότητα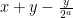 πρέπει να γίνει
πρέπει να γίνει  .
.
H απόδειξή σου για την υπόδειξη είναι σωστή μεν αλλά λείπει το εξής: για να πετύχουμε τη μετατροπή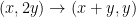 (όπου
(όπου  περιττό) κάνουμε συνεχώς την πράξη που επιτρέπεται να κάνουμε (δηλ. διπλασιάζουμε το μικρότερο ποσό σε βάρος του μεγάλου) και επειδή το σύνολο των δυνατών καταστάσεων είναι πεπερασμένο κάποια στιγμή θα «κλείσουμε κύκλο» και θα ξαναβρεθούμε στην αρχική μας κατάσταση
περιττό) κάνουμε συνεχώς την πράξη που επιτρέπεται να κάνουμε (δηλ. διπλασιάζουμε το μικρότερο ποσό σε βάρος του μεγάλου) και επειδή το σύνολο των δυνατών καταστάσεων είναι πεπερασμένο κάποια στιγμή θα «κλείσουμε κύκλο» και θα ξαναβρεθούμε στην αρχική μας κατάσταση 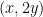 . Αν σταματήσουμε ένα βήμα πριν θα έχουμε αυτό που θέλουμε, δηλ. την κατάσταση
. Αν σταματήσουμε ένα βήμα πριν θα έχουμε αυτό που θέλουμε, δηλ. την κατάσταση  .
.
Οι περιπτώσεις σου 1 και 2 αντιστοιχούν σε περιττό και άρτιο συνολικό άθροισμα αντίστοιχα. Η περίπτωση 1 (άρτιο άθροισμα) μπορεί να μετετραπεί στην περίπτωση 4 (όλα άρτια) με μια μόνο πράξη (ανάμεσα στα δύο περιττά ποσά), οπότε δε χρειάζεται ξεχωριστή αντιμετώπιση.
Κλειδί στη μέθοδό σου είναι αυτό που ονομάζεις «ελαχιστοποίηση του περιττού», δηλ. το ότι αν έχεις τα ποσά με
με  περιττό, μπορείς να τα μετατρέψεις σε ένα ζεύγος περιττού-άρτιου ώστε να είναι ο περιττός το πολύ το μισό του αρτίου. Αυτό είναι που εξηγείς στην πρώτη παράγραφο του σχολίου 13.
περιττό, μπορείς να τα μετατρέψεις σε ένα ζεύγος περιττού-άρτιου ώστε να είναι ο περιττός το πολύ το μισό του αρτίου. Αυτό είναι που εξηγείς στην πρώτη παράγραφο του σχολίου 13.
Η υπόλοιπη απόδειξη περιέχεται στην περίπτωση 2, που είναι μια χαρά.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 27 Μαρτίου, 2010 @ 1:47 μμ