Έχουμε ένα πίνακα με στοιχεία πραγματικούς αριθμούς. Σας επιτρέπεται σε κάθε βήμα να πολλαπλασιάζετε κάθε γραμμή ή στήλη του πίνακα με -1 (να αλλάζετε δηλ. όλα τα πρόσημα σε αυτή τη γραμμή ή στήλη). Δείξτε ότι μπορείτε με αυτό τον τρόπο να πετύχετε κάθε γραμμή και κάθε στήλη του πίνακα να έχει άθροισμα
.
10 Οκτωβρίου, 2009
Πώς να αλλάξετε τα πρόσημα
6 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Υπόδειξη:
Όταν αλλάζετε τα πρόσημα μιας γραμμής ή μιας στήλης τι παθαίνει το άθροισμα όλων των στοιχείων του πίνακα;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 18 Οκτωβρίου, 2009 @ 10:01 μμ
Όταν αλλάζω το πρόσημο μίας γραμμής ή μίας στήλης που έχει άθροισμα μικρότερο του μηδενός, τότε το άθροισμα όλων των στοιχείων του πίνακα μεγαλώνει.
Όταν αλλάζω το πρόσημο μίας γραμμής, επηρεάζω τα αθροίσματα όλων των στηλών και το άθροισμα μόνο αυτής της γραμμής. Τα αθροίσματα των άλλων γραμμών μένουν ίδια.
Όταν αλλάζω το πρόσημο μίας στήλης επηρεάζω τα αθροίσματα των γραμμών και το άθροισμα μόνο αυτής της στήλης. Τα αθροίσματα των άλλων στηλών μένουν ίδια.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 19 Οκτωβρίου, 2009 @ 7:29 μμ
«Όταν αλλάζω το πρόσημο μίας γραμμής ή μίας στήλης που έχει άθροισμα μικρότερο του μηδενός, τότε το άθροισμα όλων των στοιχείων του πίνακα μεγαλώνει.»
Χρειάζεται κάπως πιο ποσοτική περιγραφή για να είναι αυτό το γεγονός χρήσιμο. Πόσο μεγαλώνει τουλάχιστον;
Μου αρέσει!Αρέσει σε 1 άτομο
Σχόλιο από Mihalis Kolountzakis — 19 Οκτωβρίου, 2009 @ 7:35 μμ
Αν στον πίνακά μας υπάρχει έστω και μια γραμμή ή μια στήλη με αρνητικό άθροισμα στοιχείων, τότε της αλλάζουμε πρόσημο (αν είναι περισσότερες, αλλάζουμε σε μια τυχαία). Τότε το άθροισμα των στοιχείων του νέου πίνακα θα υπερβαίνει το άθροισμα των στοιχείων του προηγούμενου. Ακολουθώντας αυτή τη διαδικασία δημιουργείται μια γνησίως αύξουσα ακολουθία αθροισμάτων (ενδεχομένως πεπερασμένη) και αρκει να δείξουμε ότι η ακολουθία αυτή είναι όντως πεπερασμένη. Αυτό αρκεί, διότι τότε ΔΕΝ θα μπορούμε να εναλλάξουμε τα πρόσημα κάποιας γραμμής ή στήλης έτσι, ώστε να αυξηθεί το συνολικό άθροισμα των στοιχείων του πίνακα. Άρα τότε ΔΕΝ θα υπάρχει κάποια γραμμή ούτε κάποια στήλη με αρνητικό άθροισμα στοιχείων.
Οι δυνατοί πίνακες που μπορεί να δημιουργηθούν εναλλάσοντας τυχαία τα πρόσημα του πίνακα (ένα-ένα) είναι 2^(m*n), άρα πεπερασμένοι. Συνεπώς τα δυνατά αθροίσματα των στοιχείων αυτών των πινάκων (ενδεχομένως περισσότεροι από αυτούς που εξετάζουμε) είναι πάλι πεπερασμένα.
Άρα η ακολουθία μας, αφού είναι γνησίως αύξουσα και πάιρνει τιμές από το πεπερασμένο σύνολο των δυνατών αθροισμάτων θα είναι πεπερασμένη. Ο.Ε.Δ.
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 19 Οκτωβρίου, 2009 @ 9:42 μμ
Όταν αλλάζω το πρόσημο μίας γραμμής ή μίας στήλης της οποίας το άθροισμα μικρότερο του μηδενός, τότε το άθροισμα των στοιχείων του πίνακα μεγαλώνει τόσο όσο και η απόλυτη τιμή της γραμμής ή της στήλης της οποίας άλλαξα τα πρόσημα. Συνεπώς εάν κάθε φορά που βρίσκω μία γραμμή ή στήλη με αρνητικό άθροισμα της αλλάζω το πρόσημο τότε θα πέφτω όλο και σε μεγαλύτερου αθροίσματος στοιχείων πίνακα. Προφανώς η διαδικασία αυτή δεν μπορεί να συνεχιστεί επ΄ άπειρον (όπως λέει και ο nefelh). Εγώ το προσπαθούσα με ζεύγη αριθμών (γ,σ) (γ γραμμή, σ στήλη) για κάθε στοιχείο του πίνακα, αλλά δεν έβγαλα κάτι. Ενδιαφέρον πρόβλημα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από pebox — 19 Οκτωβρίου, 2009 @ 9:50 μμ
nefelh:
Πολύ σωστά.
Ένας λίγο διαφορετικός τρόπος να δει κανείς το ίδιο επιχείρημα είναι ο εξής: σε κάθε πράξη που κάνουμε (πολλαπλασιασμός επι -1 μιας γραμμής ή μια στήλης που έχει αρνητικό άθροισμα) το άθροισμα των στοιχείων του πίνακα μεγαλώνει κατά τουλάχιστον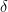 , όπου
, όπου 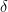 είναι ο ελάχιστος θετικός αριθμός που μπορεί να γραφεί σαν άθροισμα των στοιχείων του πίνακα με συντελεστές 0, -1 ή +1 το καθένα.
είναι ο ελάχιστος θετικός αριθμός που μπορεί να γραφεί σαν άθροισμα των στοιχείων του πίνακα με συντελεστές 0, -1 ή +1 το καθένα. το άθροισμα των απολύτων τιμών όλων των στοιχείων του πίνακα τότε θα κάνουμε το πολύ
το άθροισμα των απολύτων τιμών όλων των στοιχείων του πίνακα τότε θα κάνουμε το πολύ  βήματα.
βήματα.
Αν είναι
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 19 Οκτωβρίου, 2009 @ 9:54 μμ