Θεωρούμε δύο διανύσματα και τον
πίνακα
με
. Ποια είναι η ορίζουσα του
Για εκείνες τις τιμές του
που ο
είναι αντιστρέψιμος, ποιός είναι ο αντίστροφός του ;
25 Ιανουαρίου, 2009
Διαταραχή τάξης 1
7 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Υπόδειξη σαν γινόμενο ενός πίνακα στήλη
σαν γινόμενο ενός πίνακα στήλη  με ένα πίνακα γραμμή
με ένα πίνακα γραμμή  .
.
Προσέξτε ότι μπορούμε να γράψουμε τον πίνακα
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 8 Φεβρουαρίου, 2009 @ 5:16 μμ
Μιχάλη (Λουλάκη) χαιρετώ. Μόλις σήμερα ανακάλυψα το υπέροχο blog σας. Είμαι ο Δημήτρης Χριστοφίδης. Είχαμε γνωριστεί όταν ήσουν στο Cambridge.
Για την άσκηση: Ισχυρίζομαι ότι η ορίζουσα είναι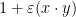 και η αντίστροφος (αν υπάρχει) είναι
και η αντίστροφος (αν υπάρχει) είναι  .
.
Για την απόδειξη, βοηθάει να παρατηρήσουμε (όπως έχεις υποδείξει) ότι και άρα
και άρα  . Εύκολα τώρα μπορεί να ελεγχθεί ότι ο πίνακας που έδωσα είναι όντως αντίστροφος.
. Εύκολα τώρα μπορεί να ελεγχθεί ότι ο πίνακας που έδωσα είναι όντως αντίστροφος.
Για την ορίζουσα δεν ξέρω αν έχεις πιο εύκολη απόδειξη. Εγώ χρησιμοποίησα ότι , άρα όλες οι ιδιοτιμές του F ισούνται είτε με 1, είτε με
, άρα όλες οι ιδιοτιμές του F ισούνται είτε με 1, είτε με 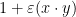 και επειδή το άθροισμά τους ισούται με
και επειδή το άθροισμά τους ισούται με 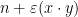 βρίσκουμε ότι ν-1 ιδιοτιμές ισούνται με 1 και μία με
βρίσκουμε ότι ν-1 ιδιοτιμές ισούνται με 1 και μία με 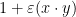 , άρα η ορίζουσα ισούται με
, άρα η ορίζουσα ισούται με 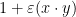 .
.
[Φαντάζομαι μπορείς να βρεις τα ιδιοδιανύσματα. Π.χ. το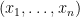 είναι το ιδιοδιάνυσμα της ιδιοτιμής
είναι το ιδιοδιάνυσμα της ιδιοτιμής 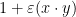 , αλλά δεν έψαξα να βρω τα υπόλοιπα.]
, αλλά δεν έψαξα να βρω τα υπόλοιπα.]
Μου αρέσει!Μου αρέσει!
Σχόλιο από demetres — 2 Μαρτίου, 2009 @ 3:11 πμ
Ωχ, συγνώμη. Πως γράφεις σε latex;
Μου αρέσει!Μου αρέσει!
Σχόλιο από demetres — 2 Μαρτίου, 2009 @ 3:15 πμ
Γεια σου Δημήτρη- και ευχαριστούμε για το σχόλιό σου. Η λύση σου είναι σωστή.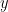 – διάστασης
– διάστασης  . Το
. Το  είναι το ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
είναι το ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή 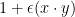 .
. είναι κάθετο στο
είναι κάθετο στο 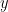 τότε ο
τότε ο 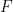 έχει μόνο
έχει μόνο  γραμμικά ανεξάρτητα ιδιοδιανύσματα και δεν είναι διαγωνιοποιήσιος.
γραμμικά ανεξάρτητα ιδιοδιανύσματα και δεν είναι διαγωνιοποιήσιος.
Ο ιδιοχώρος που αντιστοιχεί στην ιδιοτιμή 1 είναι το ορθογώνιο συμπλήρωμα του
Αν το
Για να γράψεις σε latex ανάμεσα στα σύμβολα δολλαρίου και πριν γράψεις τον κώδικα γράψε latex.
Π.χ. αν βάλεις ανάμεσα σε δολλάρια το
latex \frac{p}{q}
θα πάρεις
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 2 Μαρτίου, 2009 @ 4:22 πμ
Χαιρετώ σας και συγχαρητήρια για το blog σας. Σχετικά με την αιτιολόγηση του Δημήτρη περί των τιμών των ιδιοτιμών και της τιμής της ορίζουσας είναι και η εξής. Το άθροισμα των στοιχείων της διαγωνίου του πίνακα Π είναι ίσο με το άθροισμα των ιδιοτιμών του. Όμως ο Π δεν ειναι παρα το εξωτερικό γινόμενο των διανυσμάτων (όπως προαναφέρατε), άρα γνωρίζουμε οτι όλες οι ιδιοτιμές εκτός μιας είναι μηδέν (rank 1). Αυτή η μη μηδενική είναι ίση με το εσωτερικό γινόμενο
(όπως προαναφέρατε), άρα γνωρίζουμε οτι όλες οι ιδιοτιμές εκτός μιας είναι μηδέν (rank 1). Αυτή η μη μηδενική είναι ίση με το εσωτερικό γινόμενο 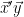 . Μετά είναι απλό να δείξει κάποιος οτι η ιδιοτιμή του
. Μετά είναι απλό να δείξει κάποιος οτι η ιδιοτιμή του  είναι
είναι 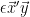 και πως όταν προσθέτουμε τον πίνακα I απλά την μεταθέτουμε κατά 1 όπως και τις μηδενικές ιδιοτιμές στο 1. Άρα η ορίζουνσα του τελικού πίνακα είναι το γινόμενο των ιδιοτιμών = 1*…*1*
και πως όταν προσθέτουμε τον πίνακα I απλά την μεταθέτουμε κατά 1 όπως και τις μηδενικές ιδιοτιμές στο 1. Άρα η ορίζουνσα του τελικού πίνακα είναι το γινόμενο των ιδιοτιμών = 1*…*1* . Γεια χαρά
. Γεια χαρά
Μου αρέσει!Μου αρέσει!
Σχόλιο από Charalampos Tsourakakis — 2 Μαρτίου, 2009 @ 10:03 πμ
Κιαυτό σωστό.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 2 Μαρτίου, 2009 @ 10:57 πμ
Δοκιμή:
Μου αρέσει!Μου αρέσει!
Σχόλιο από demetres — 2 Μαρτίου, 2009 @ 8:40 μμ