Είναι η χαρακτηριστική συνάρτηση των ρητών (1 στους ρητούς, 0 στους άρρητους) παράγωγος κάποιας συνάρτησης;
30 Νοεμβρίου, 2008
12 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Είναι η χαρακτηριστική συνάρτηση των ρητών (1 στους ρητούς, 0 στους άρρητους) παράγωγος κάποιας συνάρτησης;
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Όχι…Έστω ότι ήταν η f.Τότε, για y ρητό και ε>0, υπάρχει δ>0 ώστε για κάθε x με 0<|x-y|<δ, ισχύει ότι [f(x)-f(y)]/(x-y) είναι στο (1-ε,1+ε)
΄
Όμως για x άρρητο με 0<|x-y|<δ (που υπάρχει λόγω της πυκνότητας) εχουμε οτι το πηλίκο βρίσκεται στο (-ε,ε), άτοπο…
Μου αρέσει!Μου αρέσει!
Σχόλιο από olack — 2 Δεκεμβρίου, 2008 @ 9:55 μμ
Δεν είναι σωστό.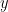 και λες ότι για κάθε
και λες ότι για κάθε  με
με 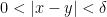 έχουμε
έχουμε
Έχεις σταθεροποιήσει έναν ρητό
Η σχέση αυτή ισχύει είτε ο είναι ρητός, είτε άρρητος. Έχεις μπερδέψει τους ρόλους των
είναι ρητός, είτε άρρητος. Έχεις μπερδέψει τους ρόλους των  και
και 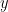 .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 3 Δεκεμβρίου, 2008 @ 3:27 μμ
‘Εχεις απόλυτο δίκιο.Θα το ξανακοιτάξω.
Μου αρέσει!Μου αρέσει!
Σχόλιο από olack — 3 Δεκεμβρίου, 2008 @ 4:09 μμ
Η απαντηση ειναι οχι. Η παρκατω αποδειξη δουλευει για καθε χαρακτηριστικη συναρτηση μιας πυκνους προσθετικης υποοομαδας των πραγματικων (γνησιας φυσικα). Εστω η χαρακτηριστικη συναρτηση των ρητων και
η χαρακτηριστικη συναρτηση των ρητων και 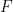 η υποθετικη της αντιπαραγωγος. Θα δειξουμε οτι η
η υποθετικη της αντιπαραγωγος. Θα δειξουμε οτι η 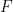 ειναι μια σταθερη συναρτηση, το οποιο ειναι προφανως ατοπο. Χωρις βλαβη της γενικοτητας υποθετουμε οτι
ειναι μια σταθερη συναρτηση, το οποιο ειναι προφανως ατοπο. Χωρις βλαβη της γενικοτητας υποθετουμε οτι 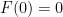 . Η βασικη παρατηρηση ειναι οτι καθε ρητος αριθμος
. Η βασικη παρατηρηση ειναι οτι καθε ρητος αριθμος  ειναι περιοδος της
ειναι περιοδος της  και αρα και της
και αρα και της 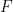 απο τον ορισμο της παραγωγου (εδω χρησιμοποιειται το γεγονος οτι οι ρητοι ειναι προσθετικη υποομαδα). Επισης, καθως
απο τον ορισμο της παραγωγου (εδω χρησιμοποιειται το γεγονος οτι οι ρητοι ειναι προσθετικη υποομαδα). Επισης, καθως 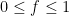 , απο το θεωρημα μεσης τιμης εχουμε οτι
, απο το θεωρημα μεσης τιμης εχουμε οτι
Αρα, λογω περιοδικοτητας, για καθε φυσικο αριθμο εχουμε οτι
εχουμε οτι
Ομως
Καθως η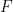 ειναι συνεχης (ως παραγωγισιμη), αυτο συνεπαγεται οτι η
ειναι συνεχης (ως παραγωγισιμη), αυτο συνεπαγεται οτι η 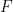 ειναι 0 στο [0,1] και αρα παντου λογω περιοδικοτητας, πραγμα ατοπο.
ειναι 0 στο [0,1] και αρα παντου λογω περιοδικοτητας, πραγμα ατοπο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 7 Δεκεμβρίου, 2008 @ 3:18 πμ
Πώς εξασφαλίζεις την περιοδικότητα της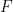 ;
; είναι μια περίοδος της
είναι μια περίοδος της  , τότε
, τότε 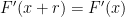 για κάθε
για κάθε  , άρα
, άρα 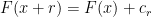 , για κάποια σταθερά
, για κάποια σταθερά  . Γιατί το
. Γιατί το  είναι μηδέν;
είναι μηδέν;
Αν
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 7 Δεκεμβρίου, 2008 @ 2:26 μμ
Εστω ρητος. Εχουμε οτι
ρητος. Εχουμε οτι 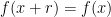 για καθε
για καθε  . Αρα για καθε
. Αρα για καθε 
Αυτο εννουσα οταν εγραψα «απο τον ορισμο της παραγωγου».
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 7 Δεκεμβρίου, 2008 @ 11:19 μμ
Τωρα που το σκεφτομαι δε χρειαζομαι τον υπολογισμο του ολοκληρωματος. Απο τη στιγμη που η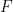 ειναι αυξουσα και περιοδικη, θα πρεπει να ειναι σταθερη. Εχουμε οτι
ειναι αυξουσα και περιοδικη, θα πρεπει να ειναι σταθερη. Εχουμε οτι  και αρα
και αρα 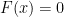 για καθε
για καθε ![x\in[0,1]](https://s0.wp.com/latex.php?latex=x%5Cin%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Τοτε
. Τοτε  ταυτοτικα λογω περιοδικοτητας.
ταυτοτικα λογω περιοδικοτητας.
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 7 Δεκεμβρίου, 2008 @ 11:31 μμ
Η υποτίθεται ότι είναι η παράγωγος της
υποτίθεται ότι είναι η παράγωγος της 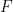 . Δεν είναι βέβαια η
. Δεν είναι βέβαια η 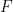 παράγωγος της παντού ασυνεχούς
παράγωγος της παντού ασυνεχούς  .
.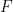 και ποια η
και ποια η  .
.
Τα όρια που γράφεις δεν έχουν νόημα. Μάλλον μπέρδεψες ποια είναι η
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 8 Δεκεμβρίου, 2008 @ 12:06 πμ
Εχετε απολυτο δικιο. Μπερδευτηκα και αλλαξα τους ρολους των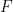 και
και  . Διορθωνω λοιπον την αποδειξη. Για καθε ρητο
. Διορθωνω λοιπον την αποδειξη. Για καθε ρητο  υπαρχει καποια σταθερα
υπαρχει καποια σταθερα  ωστε
ωστε 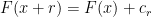 . Απο το θεωρημα μεσης τιμης εχουμε οτι
. Απο το θεωρημα μεσης τιμης εχουμε οτι  ή
ή  . Αν υπαρχει καποιος ρητος
. Αν υπαρχει καποιος ρητος  ωστε
ωστε  , τοτε απο το σχολιο (7) (καταλληλα τροποποιημενο) θα εχουμε οτι
, τοτε απο το σχολιο (7) (καταλληλα τροποποιημενο) θα εχουμε οτι  ταυτοτικα, πραγμα ατοπο. Ας υποθεσουμε λοιπον οτι
ταυτοτικα, πραγμα ατοπο. Ας υποθεσουμε λοιπον οτι  για καθε ρητο
για καθε ρητο  . Αρα
. Αρα
για καθε ρητο και, λογω συνεχειας
και, λογω συνεχειας 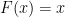 για καθε πραγματικο αριθμο
για καθε πραγματικο αριθμο  , το οποιο συνεπαγεται οτι
, το οποιο συνεπαγεται οτι  . Αυτο σημαινει οτι ολοι οι πραγματικοι ειναι ρητοι, κατι το οποιο προφανως και δεν ισχυει (εδω χρησιμοποιειται το γεγονος οτι οι ρητοι ειναι γνησιο υποσυνολο των πραγματικων. Αυτο επρεπε να χρησιμοποιηθει καπου!)
. Αυτο σημαινει οτι ολοι οι πραγματικοι ειναι ρητοι, κατι το οποιο προφανως και δεν ισχυει (εδω χρησιμοποιειται το γεγονος οτι οι ρητοι ειναι γνησιο υποσυνολο των πραγματικων. Αυτο επρεπε να χρησιμοποιηθει καπου!)
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 8 Δεκεμβρίου, 2008 @ 12:39 πμ
Πολύ σωστά. Στην πραγματικότητα, το ότι το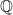 είναι… το
είναι… το 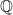 , δεν παίζει κανένα ρόλο.
, δεν παίζει κανένα ρόλο.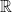 ) δεν έχει αντιπαράγωγο;
) δεν έχει αντιπαράγωγο;
Μπορείς να δείξεις ότι η χαρακτηριστική συνάρτηση οποιουδήποτε συνόλου (εκτός του ίδιου του
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 8 Δεκεμβρίου, 2008 @ 1:27 πμ
Παραθετω εδω τη λυση στο γενικοτερο ερωτημα που θεσατε.
Εστω ενα υποσυνολο των πραγματικων αριθμων. Θετουμε
ενα υποσυνολο των πραγματικων αριθμων. Θετουμε 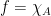 για τη χαρακτηριστικη του συναρτηση και
για τη χαρακτηριστικη του συναρτηση και  για τη χαρακτηριστικη συναρτηση του συμπληρωματος του. Εχουμε οτι
για τη χαρακτηριστικη συναρτηση του συμπληρωματος του. Εχουμε οτι  ταυτοτικα και αρα η
ταυτοτικα και αρα η  εχει αντιπαραγωγο αν, και μονο αν, η
εχει αντιπαραγωγο αν, και μονο αν, η  εχει αντιπαραγωγο. Θα δειξουμε οτι αν
εχει αντιπαραγωγο. Θα δειξουμε οτι αν
τοτε αυτο ειναι αδυνατο (σε αντιθετη περιπτωση το προβλημα εχει τετριμμενη λυση). Εστω λοιπον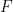 και
και  οι υποθετικες αντιπαραγωγοι των συναρτησεων
οι υποθετικες αντιπαραγωγοι των συναρτησεων  και
και  , αντιστοιχα. Χωρις βλαβη της γενικοτητας υποθετουμε οτι
, αντιστοιχα. Χωρις βλαβη της γενικοτητας υποθετουμε οτι 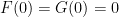 . Τοτε θα εχουμε οτι
. Τοτε θα εχουμε οτι
Εστω . Τοτε απο το θεωρημα μεσης τιμης εχουμε οτι
. Τοτε απο το θεωρημα μεσης τιμης εχουμε οτι
ή
Σε καθε περιπτωση, οι ειναι αυξουσες συναρτησεις. Αν ισχυει η (1), τοτε απο τη (*) παιρνουμε οτι
ειναι αυξουσες συναρτησεις. Αν ισχυει η (1), τοτε απο τη (*) παιρνουμε οτι  και καθως η
και καθως η  ειναι αυξουσα, η
ειναι αυξουσα, η  ειναι σταθερη στο διαστημα που οριζεται απο τα σημεια
ειναι σταθερη στο διαστημα που οριζεται απο τα σημεια 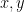 . Διαφορετικα, αν ισχυει η (2), τοτε η
. Διαφορετικα, αν ισχυει η (2), τοτε η 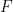 θα ειναι σταθερη σε αυτο το διαστημα. Αν τωρα εξετασουμε τι γινεται μεσα στο διαστημα
θα ειναι σταθερη σε αυτο το διαστημα. Αν τωρα εξετασουμε τι γινεται μεσα στο διαστημα ![{[0,1]}](https://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , το παραπανω επιχειρημα συνεπαγεται οτι μια εκ των
, το παραπανω επιχειρημα συνεπαγεται οτι μια εκ των 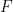 και
και  θα ειναι σταθερη σε αυτο. Χωρις βλαβη της γενικοτητας υποθετουμε οτι η
θα ειναι σταθερη σε αυτο. Χωρις βλαβη της γενικοτητας υποθετουμε οτι η 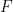 ειναι σταθερη και αρα
ειναι σταθερη και αρα 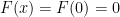 για
για ![x\in[0,1]](https://s0.wp.com/latex.php?latex=x%5Cin%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Τοτε ισχυριζομαστε οτι
. Τοτε ισχυριζομαστε οτι
(**) ταυτοτικα σε ολη την πραγματικη ευθεια.
ταυτοτικα σε ολη την πραγματικη ευθεια.
Οντως, αν υπηρχε καποιο σημειο τετοιο ωστε
τετοιο ωστε  , τοτε για τα σημεια 0 και
, τοτε για τα σημεια 0 και  η (2) δεν μπορει να ισχυει και αρα θα ισχυει η (1). Αυτο με τη σειρα του συνεπαγεται οτι η
η (2) δεν μπορει να ισχυει και αρα θα ισχυει η (1). Αυτο με τη σειρα του συνεπαγεται οτι η  ειναι σταθερα ιση με το 0 στο συγκεκριμενο διαστημα και αρα
ειναι σταθερα ιση με το 0 στο συγκεκριμενο διαστημα και αρα 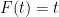 μεταξυ των 0 και
μεταξυ των 0 και  . Καθως ξερουμε οτι
. Καθως ξερουμε οτι  , θα πρεπει να εχουμε οτι
, θα πρεπει να εχουμε οτι 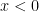 . Αυτο ομως ειναι αδυνατο, γιατι τοτε η
. Αυτο ομως ειναι αδυνατο, γιατι τοτε η 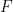 δε θα ηταν παραγωγισιμη στο σημειο 0. Επομενως, η (**) ισχυει. Παραγωγιζοντας την (**) βρισκουμε οτι
δε θα ηταν παραγωγισιμη στο σημειο 0. Επομενως, η (**) ισχυει. Παραγωγιζοντας την (**) βρισκουμε οτι  ταυτοτικα στην πραγματικη ευθεια και αρα το συνολο
ταυτοτικα στην πραγματικη ευθεια και αρα το συνολο  ειναι κενο, πραγμα που αντιβαινει στην υποθεση για αυτο το συνολο.
ειναι κενο, πραγμα που αντιβαινει στην υποθεση για αυτο το συνολο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 10 Δεκεμβρίου, 2008 @ 3:46 πμ
Πολύ σωστά. σύνολο.
σύνολο.
Ο «βαθύτερος» λόγος που ισχύουν όλα αυτά είναι ότι η παράγωγος μιας συνάρτησης μπορεί να είναι ασυνεχής, έχει όμως πάντα την ιδιότητα ενδιάμεσης τιμής. Επομένως αν κάποια συνάρτηση δεν την έχει (όπως μια χαρακτηριστική), τότε δεν μπορεί να έχει αντιπαράγωγο. Κάτι άλλο, ανεξάρτητο, το οποίο δείχνει ότι η παράγωγος δεν μπορεί να είναι «πολύ ασυνεχής» είναι το εξής. Η παράγωγος είναι κατά σημείο όριο μιας ακολουθίας συνεχών συναρτήσεων. Τέτοιες συναρτήσεις, από το θεώρημα του Baire, πρέπει να είναι συνεχείς σε ένα πυκνό
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 10 Δεκεμβρίου, 2008 @ 3:03 μμ