Για και για φυσικό αριθμό
ορίζουμε
.
Αν ακέραιος και
πρώτος αριθμός δείξτε ότι υπάρχει ακέραιος
και ακέραιος
ώστε να ισχύει
.
Για και για φυσικό αριθμό
ορίζουμε
.
Αν ακέραιος και
πρώτος αριθμός δείξτε ότι υπάρχει ακέραιος
και ακέραιος
ώστε να ισχύει
.
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Ο τελευταίος διωνυμικός συντελεστής ισούται με .
.
Αρκεί επομένως να δειχθεί ότι τα πολλαπλάσια του (όπου
(όπου  πρώτος διάφορος του
πρώτος διάφορος του 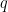 και
και 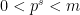 ) στο
) στο  είναι όσα και τα πολλαπλάσια του στο
είναι όσα και τα πολλαπλάσια του στο  .
.
Όντως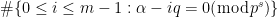
![{=\#\{i : i=\alpha q^{-1}(\bmod p^s)\}=[m / p^s]}](https://s0.wp.com/latex.php?latex=%7B%3D%5C%23%5C%7Bi+%3A+i%3D%5Calpha+q%5E%7B-1%7D%28%5Cbmod+p%5Es%29%5C%7D%3D%5Bm+%2F+p%5Es%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από ef8sof — 29 Οκτωβρίου, 2008 @ 5:18 πμ
ef8sof:
Πολύ καλή προσπάθεια αλλά νομίζω πως δεν είναι ακόμη πλήρης. Λείπει λίγη προσοχή από το μέτρημα στο τέλος.
Αποδεικνύεις για παράδειγμα ότι το πλήθος των δυνάμεων του είναι ίδιο σε αριθμητή και παρανομαστή, πράγμα που δεν ισχύει. Δες π.χ. το
είναι ίδιο σε αριθμητή και παρανομαστή, πράγμα που δεν ισχύει. Δες π.χ. το 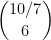 . Αυτό έχει παραπάνω 3άρια πάνω απ’ ό,τι κάτω.
. Αυτό έχει παραπάνω 3άρια πάνω απ’ ό,τι κάτω.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 29 Οκτωβρίου, 2008 @ 10:16 πμ
O συντελεστης ειναι :
[a(a-q)(a-2q)…(a-(m-1)q)]/m!*q^m.Αρκει προφανως να δειξουμε οτι m! διαιρει την ποσοτητα
[a(a-q)(a-2q)…(a-(m-1)q)].Εστω τωρα i διαφορετικο του j που ανηκουν στο {0,1,…,m-1} ετσι ωστε a-iq=a-jqmodm.Απο εδω ευκολα προκυπτει οτι i=jmodm κατι που ειναι ατοπο.Οποτε a-iq ανισοτιμοι ανα δυο modulo m.Αρα υπαρχει απεικονιση ενα προς ενα και επι σ:{0,1…,m-1}->{1,2,…,m-1,m} ετσι ωστε a-iq=σ(i)modm , i=0,1,…,m-1.Οποτε προφανως [a(a-q)(a-2q)…(a-(m-1)q)]=m!modm και το ζητουμενο αποδειχθηκε.Μαλιστα n=m.
Μου αρέσει!Μου αρέσει!
Σχόλιο από nikkaram — 9 Νοεμβρίου, 2008 @ 9:35 μμ
nikkaram:
Η προτελευταία πρότασή σου («Οπότε προφανώς …») δε συνεπάγεται αυτό που ισχυρίζεσαι.
Και μάλιστα δε μπορείς να περιμένεις ότι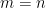 . Αν, π.χ.,
. Αν, π.χ.,  τότε δεν ισχύει.
τότε δεν ισχύει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Νοεμβρίου, 2008 @ 10:30 μμ
Ναι , βιαστηκα. Με συγχωρειτε για την ταλαιπωρια , θα το δω πιο προσεκτικα.Ευχαριστω.
Μου αρέσει!Μου αρέσει!
Σχόλιο από nikkaram — 10 Νοεμβρίου, 2008 @ 6:47 πμ
Κανένα πρόβλημα. Ο μόνος τρόπος για να μην κάνει κανείς ποτέ λάθος είναι να μην λέει ποτέ τίποτα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 10 Νοεμβρίου, 2008 @ 10:15 πμ
Μπορω να υποθεσω οτι ο q δεν διαιρει τον a?Γιατι αλλιως αναγεται στο γνωστο διωνυμικο συντελεστη των Κ ανα Μ οπου και οι δυο ακεραιοι.
Μου αρέσει!Μου αρέσει!
Σχόλιο από nikkaram — 11 Νοεμβρίου, 2008 @ 9:37 μμ
Φυσικά. Αλλιώς δεν υπάρχει τίποτα προς απόδειξη αφού ο διωνυμικός συντελεστής είναι ακέραιος.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 11 Νοεμβρίου, 2008 @ 10:37 μμ
Συμπληρωνω την ιδεα του/της ef8sof. Εστω καποια δυναμη πρωτου διαφορου του
καποια δυναμη πρωτου διαφορου του 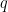 . Εστω
. Εστω  που ικανοποιει τη σχεση
που ικανοποιει τη σχεση  . Τότε γραφοντας
. Τότε γραφοντας
Επομενως, η ακριβης δυναμη του που διαρει το γινομενο
που διαρει το γινομενο 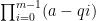 ειναι ιση με
ειναι ιση με
[αθροιζουμε (οροι γινομενου που διαιρουνται με
(οροι γινομενου που διαιρουνται με  -οροι γινομενου που ΔΕΝ διαιρουνται με
-οροι γινομενου που ΔΕΝ διαιρουνται με  ) ]
) ]
Με παρομοιο τροπο μπορουμε να δειξουμε οτι η ακριβης δυναμη του που διαρει το
που διαρει το  ειναι
ειναι
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 4 Μαΐου, 2009 @ 1:50 πμ
Πολύ ωραία.
Να διευκρινίσω εδώ ότι στην (*) χρησιμοποίησες «άθροιση κατά μέρη»: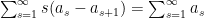 .
.
Πριν από 2-3 χρόνια είχα συναντήσει αυτό το ερώτημα. Μέχρι σήμερα δεν ήξερα αυτή τη «στοιχειώδη» λύση. Η μόνη λύση που είχα καταφέρει να σκεφτώ χρησιμοποιούσε p-αδικούς αριθμούς και μπορείτε να τη βρείτε εδώ (αγγλικά).
Στη γλώσσα των p-αδικών αριθμών είναι πολύ απλή η λύση, σχεδόν φυσιολογική αν κανείς έχει χωνέψει λίγο τη σχετική ορολογία. Αν κάποιος δεν ξέρει τι είναι αυτοί οι p-αδικοί αριθμοί τότε ελπίζω να του κεντρίσει αυτή η λύση το ενδιαφέρον για να μάθει (εγώ τουλάχιστον μαθαίνω πιο εύκολα όταν έχω κίνητρο).
Μπορείτε επίσης να δείτε το σχετικό άρθρο:
R.C. Alperin, p-adic binomial coefficients , The American Mathematical Monthly, Vol. 92, No. 8 (Oct., 1985), pp. 576-578.
, The American Mathematical Monthly, Vol. 92, No. 8 (Oct., 1985), pp. 576-578.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 4 Μαΐου, 2009 @ 8:41 πμ
Άλλη μια στοιχειώδης λύση (όχι και τόσο ουσιαστικά διαφορετική) βασισμένη πάνω στην ιδέα του nikkaram είναι η εξής: Έστω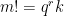 , όπου
, όπου  . Έστω τώρα
. Έστω τώρα 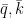 ακέραιοι ώστε
ακέραιοι ώστε  . Φυσικά,
. Φυσικά,  . Θέτουμε
. Θέτουμε  , οπότε:
, οπότε:
για κάποιο ακέραιο . Επομένως
. Επομένως 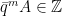 . Είναι επίσης φανερό ότι
. Είναι επίσης φανερό ότι
Εφόσον έχουμε ότι θα πρέπει
έχουμε ότι θα πρέπει  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 5 Μαΐου, 2009 @ 12:58 πμ
«Συμπαγές» αλλά τέλειο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 5 Μαΐου, 2009 @ 9:55 πμ
Μια διαφορετική λύση: Παρατηρώ ότι αρκεί να αποδείξουμε το θεώρημα για . Πράγματι, τo
. Πράγματι, τo 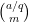 ισούται με τον συντελεστή του
ισούται με τον συντελεστή του 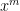 στο ανάπτυγμα
στο ανάπτυγμα
Άρα
Θα αποδείξω τώρα το ζητούμενο με επαγωγή στο .
.
Για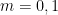 είναι προφανές. Βάζοντας όπου
είναι προφανές. Βάζοντας όπου 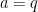 στην πιο πάνω ισότητα (για
στην πιο πάνω ισότητα (για  ) παίρνω
) παίρνω
όπου ο πρώτος όρος του αθροίσματος είναι ο μοναδικός όρος με . Άρα
. Άρα
το οποίο επαγωγικά έχει την ζητούμενη ιδότητα.
(Δεν έχω χρησιμοποιήσει πουθενά ότι ο q είναι πρώτος. Ελπίζω να μην έχω κάνει πουθενά λάθος.)
Μου αρέσει!Μου αρέσει!
Σχόλιο από Δημήτρης — 5 Μαΐου, 2009 @ 11:27 μμ
Πάρα πολύ ωραία, σωστή κι αυτή η μέθοδος.
Όντως το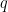 δε χρειάζεται να είναι πρώτος. Και η μέθοδος με τους p-αδικούς αριθμούς που έχω περιγράψει παραπάνω δίνει, ακριβώς όπως είναι γραμμένη, ότι οι μόνοι πρώτοι που εμφανίζονται στον παρανομαστή του
δε χρειάζεται να είναι πρώτος. Και η μέθοδος με τους p-αδικούς αριθμούς που έχω περιγράψει παραπάνω δίνει, ακριβώς όπως είναι γραμμένη, ότι οι μόνοι πρώτοι που εμφανίζονται στον παρανομαστή του  είναι αυτοί που συμμετέχουν στον ακέραιο
είναι αυτοί που συμμετέχουν στον ακέραιο 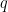 . Πολλαπλασιάζοντας μετά αριθμητή και παρανομαστή με τον κατάλληλο ακέραιο μπορούμε να εμφανίσουμε δύναμη του
. Πολλαπλασιάζοντας μετά αριθμητή και παρανομαστή με τον κατάλληλο ακέραιο μπορούμε να εμφανίσουμε δύναμη του 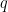 στον παρανομαστή (το κλάσμα βέβαια δεν είναι αναγκαστικά ανάγωγο μετά από αυτή την πράξη).
στον παρανομαστή (το κλάσμα βέβαια δεν είναι αναγκαστικά ανάγωγο μετά από αυτή την πράξη).
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 6 Μαΐου, 2009 @ 10:24 πμ