Αν σε μια πρόταση εναλλάξετε τις θέσεις δυο ποσοδεικτών, τότε συνήθως το νόημα αλλάζει δραματικά. Για παράδειγμα, αν σε κάποιο διαγώνισμα τον ορισμό της συγκλίνουσας ακολουθίας τον ξεκινήσετε ως εξής:
«Υπάρχει τέτοιο ώστε για κάθε
μπλα μπλα μπλα»
τότε το πιο πιθανό είναι ότι θα εξασφαλίσετε την συμμετοχή σας στην επόμενη εξεταστική. Επίσης, οι προτάσεις
«Για κάθε γυναίκα υπάρχει άντρας έτσι ώστε μπλα μπλα μπλα»
και
«Υπάρχει άντρας έτσι ώστε για κάθε γυναίκα μπλα μπλα μπλα»
είναι μάλλον διαφορετικές, εκτός κι’ αν μιλάμε για τον Brad Pitt. Παρ’ όλα αυτά, βρείτε 4 συντακτικά σωστές μαθηματικές προτάσεις (μπλα μπλα)-1, (μπλα μπλα)-2, (μπλα μπλα)-3 και (μπλα μπλα)-4 έτσι ώστε οι παρακάτω δυο συνεπαγωγές να είναι αληθείς:
«Αν υπάρχει (μπλα μπλα)-1 έτσι ώστε για κάθε (μπλα μπλα)-2 να ισχύει (μπλα μπλα)-3, τότε (μπλα μπλα)-4»
και
«Αν για κάθε (μπλα μπλα)-2 υπάρχει (μπλα μπλα)-1 έτσι ώστε να ισχύει (μπλα μπλα)-3, τότε (μπλα μπλα)-4»
Υπόδειξη:
Έστω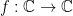 αναλυτική. Τότε:
αναλυτική. Τότε:
και
Η πρώτη πρόταση είναι προφανής. Η δεύτερη θέλει απόδειξη.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 2 Οκτωβρίου, 2008 @ 5:37 μμ
Χμ… Ίσως δεν καταλαβαίνω τι θέλει να πει η άσκηση. Το πρώτο πράγμα που σκέφτηκα πάντως διαβάζοντας την εκφώνηση είναι στην πρόταση (μπλα-μπλα)-4 να βάλω την «η γιαγιά μου είναι τρόλεϊ» (ή την 0=1 για να είναι σωστή και μαθηματικά). Η συνεπαγωγή τότε θα πρέπει να είναι αληθής. Η υπόδειξη όμως με μπαρδεύει αρκετά…
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 7 Οκτωβρίου, 2008 @ 2:37 πμ
Η άσκηση λέει ότι είναι δυνατό να εναλλάξεις τους ποσοδείκτες σε μια πρόταση και να παραμείνει αληθής (πράγμα αρκετά σπάνιο σε normal καταστάσεις)
Η υπόδειξη δίνει ένα παράδειγμα δυο τέτοιων προτάσεων. Η πρώτη είναι προφανώς αληθής: αν η νιοστή παράγωγος μιας συνάρτησης είναι μηδεν τότε είναι πολυώνυμο.
[υπάρχει ν τέτοιο για κάθε σημείο η νιοστή παράγωγος είναι μηδέν]
Η δεύτερη δεν είναι προφανής. Αν σε κάθε σημείο κάποιας τάξης παράγωγος μηδενίζεται, πάλι η συνάρτηση είναι πολυώνυμο, αλλά αυτό, τώρα, χρειάζεται απόδειξη.
[για κάθε σημείο υπάρχει ν τέτοιο ώστε η νιοστή παράγωγος είναι μηδέν]
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 7 Οκτωβρίου, 2008 @ 3:45 πμ
Η δική μου παρατήρηση είναι ότι στην περίπτωση που η πρόταση (μπλα-μπλα)-4 είναι μια πρόταση πάντοτε ψευδής, τότε η συνεπαγωγή ισχύει σε κάθε περίπτωση. Με αυτόν τον τρόπο μπορούμε να κατασκευάσουμε εύκολα άπειρες προτάσεις όπου η σειρά των ποσοδεικτών να μην έχει καμία σημασία — αφού πάντοτε θα είναι αληθείς.
—————
Ακόμα όμως και αυτό το «ακραίο παράδειγμα να μην χρησιμοποίησουμε, νομίζω πως μπορώ να δώσω έναν άλλο «αλγόριθμο» κατασκευής τέτοιων προτάσεων:
Παίρνουμε μια οποιαδήποτε αληθή πρόταση που περιέχει κάπου ποσοδείκτες (για κάθε)χ(υπάρχει)ψ , και επίσης η πρόταση (μπλα-μπλα)-4 να είναι ανεξάρτητη των χ και ψ. Τότε μπορούμε να εναλλάξουμε τους ποσοδείκτες.
Δυστυχώς δεν έχω χρόνο να το αναλύσω καλύτερα τώρα (γι’ αυτό κ αποφεύγω να γράψω σε latex)… θα επανέλθω το απόγευμα ή αύριο όμως να το κάνω πιο σαφές, σε περίπτωση που αυτό χρειάζεται.
Μία μόνον παρατήρηση: πιστεύω ότι η άσκηση λύνεται και από το παράδειγμα που έδωσα στην αρχή. Η λύση αυτή που περιέγραψα παραπάνω έχει το «πλεονέκτημα» ότι εξετάζει και μη-τετριμένες προτάσεις, που χρησιμοποιούμε διαρκώς στα μαθηματικά. Αν και με μια πρώτη ανάγνωση φαίνεται ότι τέτοιες «καθημερινές» προτάσεις δεν έχουν ποσοδείκτες με την σειρά (υπάρχει)χ(για κάθε)ψ, παρόλα αυτά αν θέλουμε να είμαστε αυστηροί, τότε πάρα πολλές φορές εμφανίζονται τέτοιοι ποσοδείκτες. Ενα παράδειγμα: στον ορισμό της συνέχειας, πόσες φορές σημειώνουμε στο τέλος (για κάθε)χ_0;;
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 7 Οκτωβρίου, 2008 @ 11:07 πμ
Η συνεπαγωγή είναι πάντα αληθής όταν η
είναι πάντα αληθής όταν η  είναι ψευδής, όχι η
είναι ψευδής, όχι η 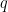 .
.
 σημαίνει
σημαίνει  .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 7 Οκτωβρίου, 2008 @ 2:09 μμ
Φυσικά έχετε δίκιο! Αυτό που θα ήθελα να γράψω είναι η πρόταση (μπλα-μπλα)-3 να είναι πάντοτε ψευδής… Ξαναθέτω λοιπόν το ερώτημα: αυτές οι περιπτώσεις δεν αποτελούν λύσεις του προβλήματος;
Τώρα αυτό που είχα υποσχεθεί στο προηγούμενο σχόλιό μου: ακόμα και χωρίς αυτή τη λύση μπορούμε (πάλι με «αλγοριθμικό»-τετριμένο τρόπο) να κατασκευάσουμε τέτοιες προτάσεις. Ένα παράδειγμα:
Βέβαια η παραπάνω πρόταση δεν έχει και μεγάλη «αξία». Όμως νομίζω ότι λύει το πρόβλημα. Εάν όντως είναι έτσι, νομίζω ότι το να γράψω άλλες 3 τέτοιες προτάσεις περιττεύει — τις κατασκευάζω από οποιαδήποτε άλλη πρότασηαντίστοιχης μορφής.
Είναι όμως αυτό που ζητάτε στην άσκηση; Ακόμα δεν έχω καταλάβει…
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 10 Οκτωβρίου, 2008 @ 2:33 πμ
Δεν καταλαβαινω τι κάνω λάθος στη latex και δε μου το διαβαζει… Και πολύ περισσότερο δεν καταλαβαίνω γιατι έχει κόψει 2 παραγράφους από αυτό που έγραψα (το έσβησα μόνος μου??). Ας το γράψουμε ξανά αυτό που λείπει να δούμε….
————————-
το παρακάτω υποτίθεται ότι έπρεπε να γραφτεί ΜΕΤΑ την μαθηματική σχέση και ΠΡΙΝ το «Βέβαια…»
————————-
Το παραπάνω είναι αληθής πρόταση (ορισμός). Βέβαια έχω σκόπιμα «ξεχάσει» κάποιους ποσοδείκτες αλλά νομίζω ότι δεν είναι εκεί η ουσία της άσκησης (είναι;;).
Προφανώς στην παραπάνω πρόταση μπορούμε να εναλλάξουμε τους ποσοδείκτες, μετατρέποντάς την σε: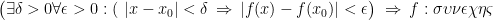
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 10 Οκτωβρίου, 2008 @ 2:49 πμ
Και ξανά δεν εμφανίζει την latex… Αν έχω κάνει κάποιο λαθός στη συνταξη ενημερώστε με τι πρέπει να αλλάξω και το postάρω ξανά…
Μου αρέσει!Μου αρέσει!
Σχόλιο από nefelh — 10 Οκτωβρίου, 2008 @ 2:51 πμ
Το παράδειγμά σου είναι σωστό.
Απλά στην υπόδειξη βρίσκονται δυο προτάσεις οι οποίες έχουν περισσότερο μαθηματικό περιεχόμενο, δηλαδή λένε κάτι μη τετριμμένο.
Μπορείς να δείξεις την δεύτερη;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 10 Οκτωβρίου, 2008 @ 12:51 μμ
Η δευτερη προταση της υποδειξης ειναι μια εφαρμογη του θεωρηματος κατηγοριας Baire. Οριζουμε Τοτε τα συνολα
Τοτε τα συνολα 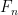 ειναι κλειστα και η ενωση τους ειναι ολο το
ειναι κλειστα και η ενωση τους ειναι ολο το 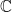 . Επομενως, απο το θεωρημα κατηγοριας Baire, θα υπαρχει καποιος φυσικος n τετοιος ωστε το συνολο
. Επομενως, απο το θεωρημα κατηγοριας Baire, θα υπαρχει καποιος φυσικος n τετοιος ωστε το συνολο 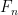 εχει μη κενο εσωτερικο. Δηλαδη, θα υπαρχει μια μπαλλα
εχει μη κενο εσωτερικο. Δηλαδη, θα υπαρχει μια μπαλλα 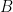 ωστε
ωστε  για καθε
για καθε 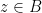 . Καθως η
. Καθως η  και αρα και η
και αρα και η 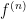 ειναι αναλυτικες, αυτο συνεπαγεται οτι
ειναι αναλυτικες, αυτο συνεπαγεται οτι  για καθε
για καθε 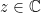 λογω θεωρηματος ταυτισμου, δηλαδη η
λογω θεωρηματος ταυτισμου, δηλαδη η  ειναι πολυωνυμο.
ειναι πολυωνυμο.
Ενα ακομα πιο ενδιαφερον προβλημα ειναι να δειχτει οτι η δευτερη προταση της υποδειξης ειναι αληθης υπο την ασθενεστερη υποθεση οτι η ειναι διαφορισιμη απειρες φορες στο
ειναι διαφορισιμη απειρες φορες στο 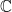 . Η αποδειξη ειναι αρκετα εκτενεστερη και πολυπλοκοτερη (τουλαχιστον αυτη που εχω υποψιν μου) και το πρωτο βημα ειναι το παραπανω επιχειρημα. Eπισης, δειτε
. Η αποδειξη ειναι αρκετα εκτενεστερη και πολυπλοκοτερη (τουλαχιστον αυτη που εχω υποψιν μου) και το πρωτο βημα ειναι το παραπανω επιχειρημα. Eπισης, δειτε
http://mathworld.wolfram.com/BaireCategoryTheorem.html
Το αστειο ειναι οτι μολις σημερα ενας φιλος μου μού ειπε για αυτο το προβλημα και καθισαμε μαζι και το λυσαμε (στο ). Λιγο αργοτερα μπηκα στο blog και ειδα αυτη την ασθενεστερη μορφη του!
). Λιγο αργοτερα μπηκα στο blog και ειδα αυτη την ασθενεστερη μορφη του!
Μου αρέσει!Μου αρέσει!
Σχόλιο από partalopoulo — 25 Οκτωβρίου, 2008 @ 2:30 πμ
Πολύ σωστά.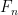 πρέπει να είναι υπεραριθμήσιμο, άρα έχει σημείο συσσώρευσης. Επομένως
πρέπει να είναι υπεραριθμήσιμο, άρα έχει σημείο συσσώρευσης. Επομένως  ταυτοτικά.
ταυτοτικά.
Μπορείς να αποφύγεις το θεώρημα τού Baire: Κάποιο από τα
Μου αρέσει!Μου αρέσει!
Σχόλιο από Themis Mitsis — 25 Οκτωβρίου, 2008 @ 11:13 πμ