Θεωρήστε την ακολουθία , με
και
για
. Δείξτε ότι όλοι οι όροι της είναι τετράγωνα ακεραίων.
12 Ιουλίου, 2008
Ακολουθία τετραγώνων
12 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Θεωρήστε την ακολουθία , με
και
για
. Δείξτε ότι όλοι οι όροι της είναι τετράγωνα ακεραίων.
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Αυτό το πρόβλημα λύνετε εύκολα αν
προσέξουμε τη λέξη «όλοι». Υποδεικνύει ότι
μάλλον πρέπει να χρησιμοποιήσουμε επαγωγή.
Οι ρίζες των 10 πρώτων όρων της ακολουθίας είναι
1, 1, 2, 5, 13, 34, 89, 233, 610, 1597
Οι ρίζες των 18 πρώτων όρων της ακολουθίας του
Fibonacci είναι
1, 1, [2], 3, [5], 8, [13], 21, [34], 55, [89],
144, [233], 377, [610], 987, [1597], 2584
Από τον 3ο όρο και μετά φαίνετε ότι η
ακολουθία έχει όρους της Fibonacci.
Θεωρώντας ότι οι ακολουθίες μας
ξεκινάνε από τον 3ο όρο με n=1, κάθε όρος
της ακολουθίας μας είναι ο F[2*n-1]^2.
Από δω και πέρα επαγωγή.
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 5 Αυγούστου, 2008 @ 8:11 μμ
Σωστή η παρατήρησή σου ότι οι όροι της ακολουθίας μας είναι τα τετράγωνα των άρτιων (αν F_0=F_1=1) όρων της ακολουθίας Fibonacci. Μένει όμως να αποδειχθεί!
Το επαγωγικό βήμα που αναφέρεις δεν είναι τετριμένο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 5 Αυγούστου, 2008 @ 10:41 μμ
Ναι είχα την εντύπωση ότι ήταν προφανές.
Λοιπόν έστω F[0]=F[1]=1 και F[n]=F[n-1]+F[n-2]
για n>=2 η ακολουθία Fibonacci.
Ελέγχουμε εύκολα ότι x[1]=F[0], x[2]=F[2].
Η επαγωγική μας υπόθεση λέει ότι:
x[n]=F[2n-2]^2 για όλα τα 2<=n<=k.
Τώρα x[k+1]=7x[k]-x[k-1]-2
Παρατηρούμε ότι ο όρος -2 δημιουργεί πρόβλημα
αφού η σχέση x[k+1]=F[2k]^2 που θέλουμε
να δείξουμε δεν πρέπει να έχει κανένα
σταθερό όρο.
Αρα ελέγχουμε επιπλέον ότι x[3]=F[4]
και γράφουμε:
x[k+1]=7*F[2k-2]^2-F[2k-4]^2-2
x[k] =7*F[2k-4]^2-F[2k-6]^2-2
Αφαιρούμε κατά μέλη και παίρνουμε:
x[k+1]-x[k]=7F[2k-2]^2-8F[2k-4]^2+F[2k-6]^2
ή ισοδύναμα:
x[k+1]=8F[2k-2]^2-8F[2k-4]^2+F[2k-6]^2
Για να έχουμε κάποια ελπίδα να δείξουμε
αυτό που θέλουμε, πρέπει να εκφράσουμε
τον όρο F[2k-6] σε σχέση με τους
F[2k-2] και F[2k-4] και μόνο.
Η ίδια σχέση με τα F[2k-2] και F[2k-4] θα μας
δώσει το F[2k].
Αρά γράφουμε:
F[k+2]=F[k+1]+F[k]
F[k+1]=F[k]+F[k-1]
F[k]=F[k-1]+F[k-2]
Κατά μέλη προσθέτουμε τις 2 πρώτες και
αφαιρούμε την τρίτη οπότε παίρνουμε:
F[k+2]=3F[k]-F[k-2]
ή ισοδύναμα:
F[k-2]=3F[k]-F[k+2]
Αρά F[2k-6]=3F[2k-4]-F[2k-2]
Αντικάθιστούμε το παραπάνω στην
έκφραση για το x[k+1] και παίρνουμε
τελικά:
x[k+1]=(3F[2k-2]-F[2k-4])^2
δηλαδή:
x[k+1]=F[2k]^2
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 7 Αυγούστου, 2008 @ 7:15 μμ
Σωστά. Επίσης η αναδρομική σχέση

με τις κατάλληλες αρχικές συνθήκες παράγει τα τετράγωνα των υπόλοιπων όρων της ακολουθίας Fibonacci.
Να μια ακόμη απόδειξη: δείτε επαγωγικά ότι . Πράγματι, για
. Πράγματι, για 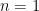 ελέγχεται εύκολα, ενώ
ελέγχεται εύκολα, ενώ
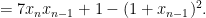 Από την επαγωγική υπόθεση αυτό είναι ίσο με
Από την επαγωγική υπόθεση αυτό είναι ίσο με 
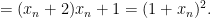 Είναι εύκολο να δείτε τώρα από τον αναδρομικό ορισμό ότι
Είναι εύκολο να δείτε τώρα από τον αναδρομικό ορισμό ότι  και επαγωγικά ότι ο
και επαγωγικά ότι ο 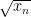 είναι ακέραιος για κάθε
είναι ακέραιος για κάθε  .
.
ΝΕΟ ΕΡΩΤΗΜΑ
Δεν είναι δύσκολο να δει κανείς πως η ακολουθία Fibonacci δεν μπορεί να οριστεί με μια γραμμική αναδρομική σχέση πρώτης τάξης. Χρησιμοποιώντας τα προαναφερόμενα βρείτε μια

μη γραμμική αναδρομική σχέση πρώτης τάξης
που ορίζει την ακολουθία Fibonacci.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 8 Αυγούστου, 2008 @ 5:43 μμ
Ψάχνουμε μια σχέση που δίνει εναλλάξ
περιττούς-άρτιους όρους της Fibonacci ή μια σχέση
που δίνει άρτιους όρους για κάποιες
αρχικές συνθήκες και περιττούς για κάποιες
άλλες?
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 9 Αυγούστου, 2008 @ 3:32 πμ
To πρώτο είχα στο μυαλό μου αλλά γιατί όχι και τα δύο?
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 10 Αυγούστου, 2008 @ 6:14 πμ
Πράγματι η σχέση

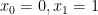


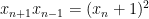

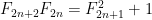
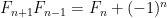

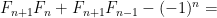


που αναφέρετε με αρχικές συνθήκες
δίνει τα τετράγωνα των υπόλοιπων όρων της
Fibonnaci.
Τώρα με επαγωγή δείχνουμε με παρόμοιο
τρόπο ότι:
Και στις δύο όμως ακολουθίες οι όροι
τους είναι τέλεια τετράγωνα
και αντιστοιχούν στη μία περίπτωση
στους όρους της Fibonacci με άρτιο δείκτη
και στην άλλη περίπτωση στους όρους
με περιττό δείκτη. Αρα από τις:
και
συμπεραίνουμε αντίστοιχα ότι:
Εικάζουμε λοιπόν για όλους τους όρους
της Fibonacci ότι:
Για n=1 ελέγχετε εύκολα.
Υπολογίζουμε:
Από την επαγωγική υπόθεση αυτό είναι ίσο με
Χρησιμοποιώντας τώρα την παραπάνω σχέση και
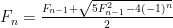
 δίνει όλους τους όρους της
δίνει όλους τους όρους της
την
καταλήγουμε σε τριώνυμο του οποίου
η λύση:
με
Fibonacci (εκτός από τον πρώτο).
Η άλλη λύση απορρίπτεται γιατί παράγει σταθερή
ακολουθία.
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 10 Αυγούστου, 2008 @ 11:38 πμ
Διόρθωση: H τελευταία ισότητα έπρεπε να . Ετσι η Fibonacci ορίζεται ως:
. Ετσι η Fibonacci ορίζεται ως:



γράφει
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 10 Αυγούστου, 2008 @ 11:52 πμ
Μία ακόμη διόρθωση:

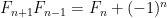
Η υπόθεση που αποδεικνύω επαγωγικά είναι η:
και όχι η:
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 10 Αυγούστου, 2008 @ 10:59 μμ
Λαμβάνοντας υπόψην τη μη γραμμική είναι όρος της
είναι όρος της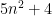
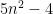 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.
αναδρομική σχέση για τη Fibonacci, προκύπτει
και το εξής αξιοσημείωτο:
Ενας αριθμός
Fibonacci αν και μόνον αν o
ή ο
Μου αρέσει!Μου αρέσει!
Σχόλιο από xatzial — 11 Αυγούστου, 2008 @ 8:02 πμ
Είναι πράγματι αξιοσημείωτο. Μόνο που δεν προκύπτει από τα προαναφερθέντα. Από την αναδρομική σχέση
(που η σωστή της μορφή αν ακολουθήσει κανείς τα βήματα που εξηγείς είναι)
πράγματι προκύπτει ότι αν ο είναι αριθμός Fibonacci τότε είτε ο
είναι αριθμός Fibonacci τότε είτε ο 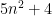 είτε ο
είτε ο 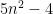 είναι τέλειο τετράγωνο. Για το αντίστροφο όμως θα πρέπει κανείς να δείξει ότι για κάθε λύση της διοφαντικής εξίσωσης δευτέρου βαθμού
είναι τέλειο τετράγωνο. Για το αντίστροφο όμως θα πρέπει κανείς να δείξει ότι για κάθε λύση της διοφαντικής εξίσωσης δευτέρου βαθμού
ο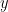 είναι αριθμός Fibonacci, και το ίδιο για την εξίσωση με -4 στο δεξί μέλος.
είναι αριθμός Fibonacci, και το ίδιο για την εξίσωση με -4 στο δεξί μέλος.
Εξισώσεις αυτού του τύπου είναι γνωστές ως εξισώσεις Pell (ή τύπου Pell). Για να μάθετε περισσότερα για αυτές- και πώς λύνονται- μπορείτε να ξεκινήσετε από εδώ:
http://mathworld.wolfram.com/PellEquation.html
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 15 Αυγούστου, 2008 @ 6:36 μμ
δινονται 3 αριθμοι 5306,3217,3124 να βρεθουν οι αριθμοι που λειπουν απο τον επομενο αριθμο 5??8
Μου αρέσει!Μου αρέσει!
Σχόλιο από jim74 — 14 Απριλίου, 2009 @ 6:26 μμ