Θεωρήστε δύο σχετικά πρώτους φυσικούς αριθμούς . Δείξτε ότι
14 Ιουνίου, 2008
4 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Θεωρήστε δύο σχετικά πρώτους φυσικούς αριθμούς . Δείξτε ότι
RSS feed for comments on this post. TrackBack URI
Εδώ θα τοποθετούμε προβλήματα μαθηματικών που θεωρούμε όμορφα. Τα πιο πολλά από αυτά δεν είναι τελείως στοιχειώδη και, κατά κανόνα, απαιτούν κάποιες γνώσεις μαθηματικών που αποκτά κανείς στο Πανεπιστήμιο (ή τουλάχιστον θα έπρεπε ...).
Στα σχόλια κάθε προβλήματος μπορείτε να γράφετε λύσεις, ιδέες, αντιρρήσεις, ερωτήσεις, σχολιασμούς, κλπ.
Αν έχετε κάποιο καλό πρόβλημα που θα θέλατε να αναρτηθεί εδώ στείλτε μας το με e-mail.
Ποιοί συνεισφέρουν προβλήματα:
| Themis Mitsis στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Όρια ορίων και η χαρακτηριστικ… | |
| Κωνσταντίνος Κουρουζ… στη Πόσα παιδιά είναι αγόρια; | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| Mihalis Kolountzakis στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη Μπορείτε να σκοτώσετε τον… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| George Rizopulos στη ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σ… | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| Κωνσταντίνος Κουρουζ… στη Απλά γραφήματα | |
| ΘΑΝΑΣΗΣ ΠΑΠΑΔΗΜΗΤΡΙΟ… στη Απλά γραφήματα |
Δημιουργήστε ένα δωρεάν ιστότοπο ή ιστολόγιο στο WordPress.com.
Θα το δείξουμε με επαγωγή στο άθροισμα . Εύκολα διαπιστώνουμε ότι ισχύει για τις πρώτες τιμές των . Έστω . Τότε, και . Πράγματι, αν το υ ήταν μηδέν , τότε το q θα διαιρούσε το p και αν υπήρχε κοινός διαιρέτης των υ,q αυτός θα διαρούσε και το p. Και στις δύο περιπτώσεις οδηγούμαστε σε άτοπο, αφού οι p,q είναι πρώτοι μεταξύ τους. Άρα,
Μου αρέσει!Μου αρέσει!
Σχόλιο από sonzi — 16 Ιουνίου, 2008 @ 5:12 μμ
Η λυση μάλλον είναι ελλiπής, μιας και δεν εμφανίζονται οι τύποι του Mathtype.
Μου αρέσει!Μου αρέσει!
Σχόλιο από sonzi — 16 Ιουνίου, 2008 @ 5:17 μμ
Θα το δείξουμε με επαγωγή στο άθροισμα p+q.
Εύκολα διαπιστώνουμε ότι ισχύει για τις πρώτες τιμές των p,q((2,3),(3,4),()4,5).
Έστω p=πq+υ με 0<=υ<q. Τότε, το υ είναι διάφορο του μηδενός και μκδ(υ,q)=1. Πράγματι, αν το υ ήταν μηδέν , τότε το q θα διαιρούσε το p και αν υπήρχε κοινός διαιρέτης των υ,q αυτός θα διαρούσε και το p. Και στις δύο περιπτώσεις οδηγούμαστε σε άτοπο, αφού οι p,q είναι πρώτοι μεταξύ τους.
Άρα,
[p/q]+[2p/q]+…+[(q-1)p/q]= [πq+υ/q]+[( πq+υ)/q]+…+[(q-1)( πq+υ)/q]=
π+[υ/q]+2π+[2υ/q]+…+(q-1)π+[(q-1)υ/q]=
(1+2+…+(q-1))π+[υ/q]+ [2υ/q]+…+ [(q-1)υ/q]={Υπόθεση Επαγωγής}
q(q-1)π/2+(q-1)(υ-1)/2=(q-1)(πq+υ-1)/2=
(q-1)(p-1)/2, που είναι το ζητούμενο
Μου αρέσει!Μου αρέσει!
Σχόλιο από sonzi — 17 Ιουνίου, 2008 @ 4:11 μμ
Σωστή η απάντησή σου- αυτό που κάνεις είναι στην ουσία επαγωγή επί του (για
(για 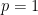 η σχέση είναι προφανής.) Δείτε και μια ακόμη λύση:
η σχέση είναι προφανής.) Δείτε και μια ακόμη λύση:
Θεωρήστε τα ζευγάρια με συντεταγμένες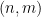 ώστε
ώστε  και
και  . Πόσα από αυτά βρίσκονται κάτω από την ευθεία που ενώνει το (0,0) με το
. Πόσα από αυτά βρίσκονται κάτω από την ευθεία που ενώνει το (0,0) με το 
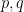 είναι σχετικά πρώτοι κανένα τέτοιο σημείο δεν ανήκει στην ευθεία, ενώ από την άλλη το
είναι σχετικά πρώτοι κανένα τέτοιο σημείο δεν ανήκει στην ευθεία, ενώ από την άλλη το 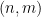 είναι κάτω από την ευθεία αν και μόνο αν το
είναι κάτω από την ευθεία αν και μόνο αν το  είναι πάνω από την ευθεία. Άρα κάτω από την ευθεία βρίσκονται ακριβώς τα μισά, δηλαδή
είναι πάνω από την ευθεία. Άρα κάτω από την ευθεία βρίσκονται ακριβώς τα μισά, δηλαδή 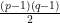 σημεία.
σημεία.
Αν τα μετρήσει κανείς κατά στήλη παίρνει ακριβώς την παράσταση στο αριστερό μέλος. Επειδή οι
Δεν είναι δύσκολο να δείτε και πώς αλλάζει η ταυτότητα αν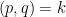 . Το δεξί μέλος της ταυτότητας πρέπει να γίνει
. Το δεξί μέλος της ταυτότητας πρέπει να γίνει 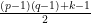 .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 17 Ιουνίου, 2008 @ 9:47 μμ