Θεωρήστε μια ακολουθία από ανεξάρτητες ισόνομες τυχαίες μεταβλητές με εκθετική κατανομή (με μέση τιμή 1). Ορίζουμε
. Υπολογίστε το
και χρησιμοποιήστε αυτό το αποτέλεσμα για να υπολογίσετε το ολοκλήρωμα
21 Μαΐου, 2008
Μέγιστο εκθετικών
17 Σχόλια »
RSS feed for comments on this post. TrackBack URI
Υπόδειξη:
Αν υπολογίσετε το όριο που προαναφέρεται, δεν είναι δύσκολο να δείτε ότι το ολοκλήρωμα είναι το όριο της![E\big[M_n-\ln(n)\big].](https://s0.wp.com/latex.php?latex=E%5Cbig%5BM_n-%5Cln%28n%29%5Cbig%5D.&bg=ffffff&fg=000000&s=0&c=20201002)
Θυμηθείτε την πάντα πολύ χρήσιμη σχέση που συνδέει τις «ουρές» μιας θετικής τ.μ. με τo ολοκλήρωμά της
![\displaystyle E[X]=\int_0^\infty P[X>x]dx](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+E%5BX%5D%3D%5Cint_0%5E%5Cinfty+P%5BX%3Ex%5Ddx&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Κι αν τώρα μια τ.μ. δεν είναι θετική δεν πειράζει- πάντα διασπάται στο θετικό και το αρνητικό της μέρος.
Βρείτε τώρα έναν άλλο τρόπο για να συνδέσετε αυτές τις αναμενόμενες τιμές για διαδοχικές τιμές του .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από loulakis — 1 Ιουνίου, 2008 @ 2:16 μμ
Νέα υπόδειξη:
Γράψτε τώρα την αναμενόμενη τιμή
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 3 Ιουλίου, 2008 @ 10:35 μμ
Αφού οι υποδείξεις δεν βοήθησαν να λυθεί το πρόβλημα θα σας δώσω ένα έξτρα κίνητρο- την τιμή του ολοκληρώματος:
όπου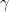 είναι η σταθερά του Euler.
είναι η σταθερά του Euler.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 26 Αυγούστου, 2008 @ 3:32 μμ
Δε βρίσκω την ίδια ολοκληρωτική αναπαράσταση για το γ (οπότε κάπου κάνω λάθος αλλα δε το βρισκω).
Παρ’ολα αυτά, μια ιδέα είναι η εξής:
Λόγω ανεξαρτησίας, έχουμε
![\mathbb{P}[M_n \leq t] = ( \mathbb{P}[X \leq t] )^n = (1 - e^{-t})^n](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BM_n+%5Cleq+t%5D+%3D+%28+%5Cmathbb%7BP%7D%5BX+%5Cleq+t%5D+%29%5En+%3D+%281+-+e%5E%7B-t%7D%29%5En+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
![\mathbb{E}[M_n] = \int_{0}^{\infty} \mathbb{P}{M_n > t} dt = \int_{0}^{\infty} 1 - (1-e^{-t})^n =](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n%5D+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+%5Cmathbb%7BP%7D%7BM_n+%3E+t%7D+dt+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+1+-+%281-e%5E%7B-t%7D%29%5En+%3D+&bg=ffffff&fg=000000&s=0&c=20201002)
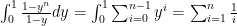
![\lim_{n \rightarrow \infty} \mathbb{E}[M_n - \ln(n)] = \lim_{n \rightarrow \infty} (\sum_{i=1}^{n} \frac{1}{i} - \ln(n) ) = \gamma.](https://s0.wp.com/latex.php?latex=%5Clim_%7Bn+%5Crightarrow+%5Cinfty%7D+%5Cmathbb%7BE%7D%5BM_n+-+%5Cln%28n%29%5D+%3D+%5Clim_%7Bn+%5Crightarrow+%5Cinfty%7D+%28%5Csum_%7Bi%3D1%7D%5E%7Bn%7D+%5Cfrac%7B1%7D%7Bi%7D+-+%5Cln%28n%29+%29+%3D+%5Cgamma.+&bg=ffffff&fg=000000&s=0&c=20201002)
![\mathbb{P}[M_n \leq \ln n + x] = (1 - \frac{e^{-x}}{n})^n \rightarrow e^{-e^{-x}}](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BM_n+%5Cleq+%5Cln+n+%2B+x%5D+%3D+%281+-+%5Cfrac%7Be%5E%7B-x%7D%7D%7Bn%7D%29%5En+%5Crightarrow+e%5E%7B-e%5E%7B-x%7D%7D+&bg=ffffff&fg=000000&s=0&c=20201002) ή
ή
![\mathbb{P}[M_n > \ln n + x] = 1- (1 - \frac{e^{-x}}{n})^n \rightarrow 1- e^{-e^{-x}}](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5BM_n+%3E+%5Cln+n+%2B+x%5D+%3D+1-+%281+-+%5Cfrac%7Be%5E%7B-x%7D%7D%7Bn%7D%29%5En+%5Crightarrow+1-+e%5E%7B-e%5E%7B-x%7D%7D+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Επίσης
που μας δίδει
Άρα,
Τώρα![\mathbb{E}[M_n - \ln(n)] = \int_{0}^{\infty} 1- (1 - \frac{e^{-x}}{n})^n](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n+-+%5Cln%28n%29%5D+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+1-+%281+-+%5Cfrac%7Be%5E%7B-x%7D%7D%7Bn%7D%29%5En+&bg=ffffff&fg=000000&s=0&c=20201002)
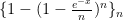 είναι μονότονη.
είναι μονότονη.![\gamma = \lim_{n \rightarrow \infty}\mathbb{E}[M_n - \ln(n)] = \int_{0}^{\infty} 1 - e^{-e^{-x}}](https://s0.wp.com/latex.php?latex=%5Cgamma+%3D+%5Clim_%7Bn+%5Crightarrow+%5Cinfty%7D%5Cmathbb%7BE%7D%5BM_n+-+%5Cln%28n%29%5D+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+1+-+e%5E%7B-e%5E%7B-x%7D%7D+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
και η ακολουθία
Άρα
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 19 Ιανουαρίου, 2011 @ 2:41 μμ
Ο λόγος που δεν βρίσκεις την ολοκληρωτική αναπαράσταση είναι ότι ο τύπος
είναι σωστός όταν η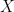 είναι μη αρνητική τ.μ., κάτι που δεν συμβαίνει για την
είναι μη αρνητική τ.μ., κάτι που δεν συμβαίνει για την 
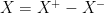
 είναι μη αρνητικές.
είναι μη αρνητικές.
που τον εφαρμόζεις. Είναι εύκολο όμως να τροποποιήσεις τον παραπάνω τύπο για γενική τ.μ. αφού
και οι
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 20 Ιανουαρίου, 2011 @ 12:56 μμ
Γράφουμε
![\mathbb{E}[M_n - \ln(n)] = \mathbb{E}[ (M_n - \ln(n))^{+}] - \mathbb{E}[(M_n - \ln(n))^{-}] = \int_{0}^{\infty} \mathbb{P}[(M_n - \ln(n))^{+}>t] - \mathbb{P}[(M_n- \ln(n) )^{-} > t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n+-+%5Cln%28n%29%5D+%3D+%5Cmathbb%7BE%7D%5B+%28M_n+-+%5Cln%28n%29%29%5E%7B%2B%7D%5D+-+%5Cmathbb%7BE%7D%5B%28M_n+-+%5Cln%28n%29%29%5E%7B-%7D%5D+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+%5Cmathbb%7BP%7D%5B%28M_n+-+%5Cln%28n%29%29%5E%7B%2B%7D%3Et%5D+-+%5Cmathbb%7BP%7D%5B%28M_n-+%5Cln%28n%29++%29%5E%7B-%7D+%3E+t%5D+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
 αν και μόνο αν
αν και μόνο αν 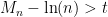 και
και
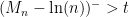 αν και μόνο αν
αν και μόνο αν ![M_n - \ln(n) t] - \mathbb{P}[M_n - \ln(n) < -t] \; dt \rightarrow \int_{0}^{\infty} 1 - e^{-e^{-t}} - e^{-e^t}](https://s0.wp.com/latex.php?latex=M_n+-+%5Cln%28n%29+t%5D+-+%5Cmathbb%7BP%7D%5BM_n+-+%5Cln%28n%29+%3C+-t%5D+%5C%3B+dt+%5Crightarrow+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+1+-+e%5E%7B-e%5E%7B-t%7D%7D+-+e%5E%7B-e%5Et%7D+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Τώρα
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 23 Ιανουαρίου, 2011 @ 5:37 μμ
Δεν εμφανίστηκε ολόκληρο το επιχείρημα.
Στην 6η γραμμή γίνεται η παρατήρηση ότι
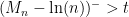 ανν
ανν 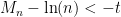
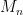 .
.
οπότε οι πιθανότητες στο ολοκλήρωμα της 2η,3η γραμμής μπορούν να υπολογιστούν
μέσω της συνάρτησης κατανομής της
Εναλλάσσουμε όριο και ολοκλήρωμα και παίρνουμε το ζητούμενο.
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 23 Ιανουαρίου, 2011 @ 8:03 μμ
Ωραία, αποδείξατε λοιπόν μέχρι τώρα ότι
Ας υπολογίσουμε τώρα την ίδια μέση τιμή με βάση την Υπόδειξη στο Σχόλιο 2. Θα πρέπει να βρείτε ότι
είναι ίση με τη σταθερά του Euler.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 24 Ιανουαρίου, 2011 @ 9:48 μμ
Χμ..
![\displaystyle \gamma = \lim \mathbb{E}[M_n - \ln(n)] = \int_{0}^{\infty} 1 - e^{-e^{-x}} - e^{-e^x} \; dx](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cgamma+%3D+%5Clim+%5Cmathbb%7BE%7D%5BM_n+-+%5Cln%28n%29%5D+%3D+%5Cint_%7B0%7D%5E%7B%5Cinfty%7D+1+-+e%5E%7B-e%5E%7B-x%7D%7D+-+e%5E%7B-e%5Ex%7D+%5C%3B+dx+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Θα έλεγα πως έχουμε αποδείξει ότι
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 24 Ιανουαρίου, 2011 @ 10:35 μμ
Ναι, έχεις απόλυτο δίκιο. Δεν πρόσεξα την αρχή του σχολίου 4.
Πολύ ωραία!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 24 Ιανουαρίου, 2011 @ 10:40 μμ
Θα ήθελα να σας κάνω μια ερώτηση, σχετική με το πρόβλημα.
Φαντάζομαι δεν είμαι ο πρώτος που ρωτάει. Απλά δεν έχω ιδέα από που να αρχισω να ψάχνω.
Μπορούμε να εκτιμήσουμε τον μέσο όρο του μεγίστου εκθετικών κατανομών όπου
όπου 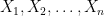
![\mathbb{E}[M_n]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n%5D&bg=ffffff&fg=000000&s=0&c=20201002) ;
;
οι οποίες δεν είναι αναγκαστικά ανεξάρτητες ;
Δηλ, αν
είναι εκθετικά κατανεμημένες, μπορούμε να πούμε κάτι για την μέγιστη δυνατή τιμή της
Ευχαριστώ!
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 27 Μαρτίου, 2012 @ 5:07 μμ
Μια ιδέα θα ήταν να χρησιμοποιήσετε το σχόλιο 2. Αν μπορείτε να πείτε κάτι για την δεσμευμένη κατανομή της δοθέντων των
δοθέντων των 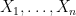 , ίσως μπορείτε να υπολογίσετε τη μέση τιμή του δεξιού μέλους αφού πρώτα υπολογίσετε την δεσμευμένη μέση τιμή του.
, ίσως μπορείτε να υπολογίσετε τη μέση τιμή του δεξιού μέλους αφού πρώτα υπολογίσετε την δεσμευμένη μέση τιμή του.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 1 Απριλίου, 2012 @ 6:33 μμ
Προσπάθησα να χρησιμοποιήσω το σχόλιο 2, αλλά δε τα καταφερα.
Παρ’όλα αυτά, νομίζω το ερώτημα μπορεί να απαντηθεί ως εξής:
Έστω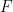 η συνάρτηση κατανομής της
η συνάρτηση κατανομής της  .
.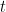 ισχύει
ισχύει
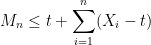
![\displaystyle \mathbb{E}[M_n] \leq t + n \int_{t}^{\infty} (1 - F(x)) \; dx,](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathbb%7BE%7D%5BM_n%5D+%5Cleq+t+%2B+n+%5Cint_%7Bt%7D%5E%7B%5Cinfty%7D+%281+-+F%28x%29%29+%5C%3B+dx%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
 . Διαφορίζοντας το δεξιό μέλος
. Διαφορίζοντας το δεξιό μέλος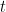 , βρίσκουμε ότι παίρνει την ελάχιστη
, βρίσκουμε ότι παίρνει την ελάχιστη . Οπότε
. Οπότε
![\displaystyle \mathbb{E}[M_n] \leq 1 + \log n](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathbb%7BE%7D%5BM_n%5D+%5Cleq+1+%2B+%5Clog+n+&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Για κάθε πραγματικό αριθμό
που δίδει ότι
για κάθε
της άνω σχέσης ως προς
τιμή της στο
Νομίζω ότι είναι αξιοσημείωτο το γεγονός ότι όπως και να δεσμεύσει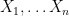 η μέγιστη δυνατή τιμή της
η μέγιστη δυνατή τιμή της ![\mathbb{E}[M_n]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n%5D&bg=ffffff&fg=000000&s=0&c=20201002)
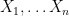 .
.
κανέις τις
είναι (περίπου) όση και στην περίπτωση ανεξάρτητων
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 23 Απριλίου, 2012 @ 11:37 μμ
Μου ξέφυγε ένα + στο

Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 23 Απριλίου, 2012 @ 11:41 μμ
Πολύ ωραία η εκτίμησή σου. Πάντως δεν είναι κάτι ιδιαίτερο αυτό το αποτέλεσμα για την εκθετική κατανομή- για οποιαδήποτε περιθώρια κατανομή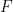 των
των  ισχύει ότι
ισχύει ότι ![\mathbb{E}\big[M_n\big]\le C\mathbb{E}_I\big[M_n\big]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cbig%5BM_n%5Cbig%5D%5Cle+C%5Cmathbb%7BE%7D_I%5Cbig%5BM_n%5Cbig%5D&bg=ffffff&fg=000000&s=0&c=20201002) , όπου η μέση τιμή αριστερά λαμβάνεται ως προς μια αυθαίρετη από κοινού κατανομή, η μέση τιμή δεξιά λαμβάνεται ως προς την κατανομή γινόμενο και η
, όπου η μέση τιμή αριστερά λαμβάνεται ως προς μια αυθαίρετη από κοινού κατανομή, η μέση τιμή δεξιά λαμβάνεται ως προς την κατανομή γινόμενο και η 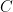 είναι μια απόλυτη σταθερά που δεν εξαρτάται ούτε από το
είναι μια απόλυτη σταθερά που δεν εξαρτάται ούτε από το  , ούτε από την
, ούτε από την 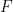 .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 24 Απριλίου, 2012 @ 3:38 πμ
Ενδιαφέρον..![\mathbb{E}[M_n] \leq C \mathbb{E}_{I}[M_n]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BM_n%5D+%5Cleq+C+%5Cmathbb%7BE%7D_%7BI%7D%5BM_n%5D&bg=ffffff&fg=000000&s=0&c=20201002) ;
;
Μπορείτε να δώσετε μια υπόδειξη ή κάποια
αναφορά σχετική με την ανισότητα
Ευχαριστώ !
Μου αρέσει!Μου αρέσει!
Σχόλιο από henk&christos — 24 Απριλίου, 2012 @ 12:44 μμ
Η βασική ιδέα -όπως ωραία παρατήρησε και ο henk- είναι ότι όποια κι αν είναι η από κοινού κατανομή, η ουρά του μεγίστου ικανοποιεί την![\mathbb{P}\big[M_n>x\big]\le 1\wedge n\bar{F}(x)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%5Cbig%5BM_n%3Ex%5Cbig%5D%5Cle+1%5Cwedge+n%5Cbar%7BF%7D%28x%29&bg=ffffff&fg=000000&s=0&c=20201002) . Για μεγάλα
. Για μεγάλα  το πάνω φράγμα σχεδόν πιάνει η ουρά του μεγίστου ανεξάρτητων τ.μ.
το πάνω φράγμα σχεδόν πιάνει η ουρά του μεγίστου ανεξάρτητων τ.μ.  .
.
Μπορείτε να δείτε την ανισότητα χρησιμοποιωντας την προσέγγιση του henk&christos ως εξής (ας υποθέσουμε για απλότητα ότι έχουμε θετικές τ.μ.)
![\displaystyle\mathbb{E}_I\big[M_n\big]=\int_0^\infty \mathbb{P}_I\big[M_n>x\big]dx=\int_0^\infty 1-F(x)^ndx=\int_0^t+\int_t^\infty 1-F(x)^n dx\ge \big(1-F(t)^n\big)\big(t+\frac{1}{\bar{F}(t)}\int_t^\infty\bar{F}(x)dx.\big)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cmathbb%7BE%7D_I%5Cbig%5BM_n%5Cbig%5D%3D%5Cint_0%5E%5Cinfty+%5Cmathbb%7BP%7D_I%5Cbig%5BM_n%3Ex%5Cbig%5Ddx%3D%5Cint_0%5E%5Cinfty+1-F%28x%29%5Endx%3D%5Cint_0%5Et%2B%5Cint_t%5E%5Cinfty+1-F%28x%29%5En+dx%5Cge+%5Cbig%281-F%28t%29%5En%5Cbig%29%5Cbig%28t%2B%5Cfrac%7B1%7D%7B%5Cbar%7BF%7D%28t%29%7D%5Cint_t%5E%5Cinfty%5Cbar%7BF%7D%28x%29dx.%5Cbig%29&bg=ffffff&fg=000000&s=0&c=20201002)
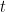 όπως στο σχόλιο 13.
όπως στο σχόλιο 13.
Στην συνέχεια επιλέγουμε το
Πάντως είναι κάτι που κι εγώ τώρα έμαθα μαζί με εσάς!
Μου αρέσει!Μου αρέσει!
Σχόλιο από Michalis Loulakis — 24 Απριλίου, 2012 @ 10:08 μμ