Αντιγράφω από την ιστοσελίδα ενός μαθήματος Μιγαδικής Ανάλυσης που δίδαξα το 1997:
Βαθμολογικό σύστημα: Εστω I ο βαθμός της εξέτασης του Ιανουαρίου, M ο βαθμός της προόδου και T ο βαθμός των ασκήσεων.
Ο τελικός βαθμός για την περίοδο του Ιανουαρίου θα είναι το μέγιστο των:
- I
- 0.6 I + 0.4 M
- 0.6 I + 0.4 T
- 0.6 I + 0.2 M + 0.2 T
Για την περίοδο Σεπτεμβρίου ο τελικός βαθμός είναι αυτός της εξέτασης και μόνο.
Ασκηση 1: Μπορείτε να παραλείψετε μια από τις παραπάνω 4 ποσότητες χωρίς να αλλάξει το βαθμολογικό σύστημα για την περίοδο Ιανουαρίου;
Μπορείτε να λύσετε αυτή την άσκηση;
Δεν είμαι μαθηματικός και θα το πω περιφραστικά 🙂
max(0.6I + 0.4M, 0.6I + 0.4T) -> max(M,T)
max(0.6I + 0.2M + 0.2T , 0.6I + 0.4T) -> max(M,T) ,
Άρα η τέταρτη ποσότητα δεν χρειάζεται!
Μου αρέσει!Μου αρέσει!
Σχόλιο από woci — 9 Μαΐου, 2008 @ 12:38 μμ
Σωστά. Να το γράψω λίγο πιο καθαρά:
Αν τότε η 2η ποσότητα είναι
τότε η 2η ποσότητα είναι 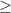 από τις 3,4.
από τις 3,4.
Αλλιώς, αν δηλ.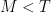 τότε η 3η ποσότητα είναι μεγαλύτερη από τις 2, 4.
τότε η 3η ποσότητα είναι μεγαλύτερη από τις 2, 4.
Άρα σε καμιά περίπτωση δε χρειάζεται η 4.
Ας γράψουμε τους συντελεστές των σε διανύσματα ως εξής:
σε διανύσματα ως εξής:
Παρατηρείστε ότι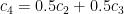 και ότι αυτό σημαίνει ότι ο 4ος τρόπος βαθμολόγησης δίνει πάντα το μέσο όρο των 2 και 3, και άρα δε μπορεί να είναι μεγαλύτερος και από τους δύο αυτούς τρόπους.
και ότι αυτό σημαίνει ότι ο 4ος τρόπος βαθμολόγησης δίνει πάντα το μέσο όρο των 2 και 3, και άρα δε μπορεί να είναι μεγαλύτερος και από τους δύο αυτούς τρόπους.
Μπορείτε να φτιάξετε 4 τρόπους βαθμολόγησης όπως παραπάνω (συντελεστές δηλ. για τις τρεις μεταβλητές ) έτσι ώστε το συνολικό βάρος του κάθε τρόπου να είναι 1 και να μην «περισσεύει» κανείς τρόπος;
) έτσι ώστε το συνολικό βάρος του κάθε τρόπου να είναι 1 και να μην «περισσεύει» κανείς τρόπος;
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Μαΐου, 2008 @ 1:01 μμ
Μπορούμε να πάρουμε τους εξής τέσσερις τρόπους:
1. 0,5 Ι + 0,5 Μ
2. 0,5 Ι + 0,5 Τ
3. 0,5 Μ + 0,5 Τ
4. 0,8 Ι + 0,1 Μ + 0,1 Τ
Αν (Ι,Μ,Τ)=(10,10,0) συμφέρει ο πρώτος, αν (Ι,Μ,Τ)=(10,0,10) συμφέρει ο δεύτερος, αν (Ι,Μ,Τ)=(0,10,10) συμφέρει ο τρίτος, ενώ αν (Ι,Μ,Τ)=(10,9,8 ) βγάζει μεγαλύτερο τελικό βαθμό ο τέταρτος, οπότε κανένας τρόπος βαθμολόγησης δε περισσεύει.
Με πέντε τρόπους;
Ποιός είναι ο μέγιστος αριθμός τρόπων βαθμολόγησης που μπορούμε να έχουμε ώστε κανένας να μην «περισσεύει»;
Μου αρέσει!Μου αρέσει!
Σχόλιο από steliosdes — 9 Μαΐου, 2008 @ 9:04 μμ
Ωραία.
Μπορείτε να δώσετε κάποια γεωμετρική συνθήκη, όσο το δυνατό πιο απλή, για τα διανύσματα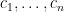 ώστε να μην «περισσεύει» κανείς από τους τρόπους βαθμολόγησης;
ώστε να μην «περισσεύει» κανείς από τους τρόπους βαθμολόγησης;
Με αυτό θα ξεκαθαρίσετε τι γίνεται με το .
.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 9 Μαΐου, 2008 @ 10:13 μμ
Αν ορίσουμε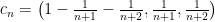 τότε ισχύει ότι
τότε ισχύει ότι
ή με άλλα λόγια ότι για κάθε υπάρχει βαθμολογία που καθιστά τον
υπάρχει βαθμολογία που καθιστά τον  -ιοστό τρόπο βαθμολόγησης συμφερότερο, δηλαδή κανένας τρόπος βαθμολόγησης δε περισσεύει.
-ιοστό τρόπο βαθμολόγησης συμφερότερο, δηλαδή κανένας τρόπος βαθμολόγησης δε περισσεύει.
Πιο συγκεκριμένα μπορούμε να πάρουμε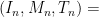
 οπότε να ισχύει
οπότε να ισχύει
Με βάση τα παραπάνω καταλήγουμε στο συμπέρασμα ότι το πλήθος των τρόπων βαθμολόγησης μπορεί να γίνει οσοδήποτε μεγάλο θέλουμε.
Μου αρέσει!Μου αρέσει!
Σχόλιο από steliosdes — 11 Μαΐου, 2008 @ 3:32 πμ
Όντως μπορούμε να πάρουμε το οσοδήποτε μεγάλο. Όχι μόνο αυτό, αλλά μπορουμε να πάρουμε και
οσοδήποτε μεγάλο. Όχι μόνο αυτό, αλλά μπορουμε να πάρουμε και  (αυτό είναι βέβαια διαφορετικό από το να μπορούμε να το πάρουμε οσοδήποτε μεγάλο).
(αυτό είναι βέβαια διαφορετικό από το να μπορούμε να το πάρουμε οσοδήποτε μεγάλο).
Όμως θα επανέλθω στο προηγούμενό μου ερώτημα:
Βρείτε ένα τρόπο να κρίνετε αν ένα από τα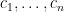 περισσεύει. Αλλιώς, διατυπώστε μια συνθήκη για τα
περισσεύει. Αλλιώς, διατυπώστε μια συνθήκη για τα 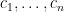 ώστε να μην περισσεύει κανένα.
ώστε να μην περισσεύει κανένα.
Για ξεκίνημα σκεφτείτε τι γίνεται αν, για παράδειγμα,
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 11 Μαΐου, 2008 @ 12:32 μμ
Αρκεί να μη γράφετε κάποιο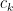 ως γραμμικός συνδυασμός κάποιον άλλων όρων με θετικούς συντελεστές, γιατί τότε το
ως γραμμικός συνδυασμός κάποιον άλλων όρων με θετικούς συντελεστές, γιατί τότε το 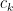 θα περισσεύει.
θα περισσεύει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από steliosdes — 11 Μαΐου, 2008 @ 2:13 μμ
Αν λοιπόν κάποιο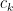 γράφεται ως γραμμικός συνδυασμός με θετικούς συντελεστές κάποιων άλλων
γράφεται ως γραμμικός συνδυασμός με θετικούς συντελεστές κάποιων άλλων  , τότε, επειδή όλα τα
, τότε, επειδή όλα τα 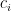 έχουν άθροισμα συντεταγμένων 1, έπεται ότι το άθροισμα των συντελεστών στο γραμμικό συνδυασμό θα είναι 1.
έχουν άθροισμα συντεταγμένων 1, έπεται ότι το άθροισμα των συντελεστών στο γραμμικό συνδυασμό θα είναι 1.
Ένας τέτοιος γραμμικός συνδυασμός (μη αρνητικοί συντελεστές, άθροισμα 1) λέγεται κυρτός συνδυασμός και παίζει το ρόλο γενικευμένου μέσου όρου.
Είναι πολύ απλό να δει κανείς ότι ένα τέτοιο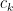 περισσεύει.
περισσεύει.
Μένει όμως να δειχτεί ότι ένα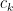 που δε γράφεται ως κυρτός συνδυασμός άλλων
που δε γράφεται ως κυρτός συνδυασμός άλλων  δεν περισσεύει.
δεν περισσεύει.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 11 Μαΐου, 2008 @ 3:48 μμ
Υπόδειξη:
Τα σημεία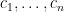 ανήκουν όλα στο επίπεδο
ανήκουν όλα στο επίπεδο  . Υποθέστε ότι κανένα από τα
. Υποθέστε ότι κανένα από τα 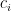 δε γράφεται ως κυρτός συνδυασμός άλλων σημείων
δε γράφεται ως κυρτός συνδυασμός άλλων σημείων  . Τα σημεία
. Τα σημεία 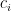 είναι τότε κορυφές ενός κυρτού πολυγώνου.
είναι τότε κορυφές ενός κυρτού πολυγώνου.
Δείξτε ότι δεν περισσεύει κανένα.
Μου αρέσει!Μου αρέσει!
Σχόλιο από Mihalis Kolountzakis — 13 Μαΐου, 2008 @ 1:50 πμ